An equilateral triangle is a triangle that has all sides of equal lengths. For example, a triangle that has all its sides 10 cm long is an equilateral triangle. Since all three sides are equal, the three interior angles also have the same measure. Thus, we can also think of an equilateral triangle as a triangle that has three 60-degree angles.
Here, we will look at a definition of equilateral triangles. Also, we will learn about the fundamental properties of these triangles and we will look at some of their most important formulas. Finally, we will use these formulas to solve some problems.
GEOMETRY
Relevant for…
Learning about the characteristics of equilateral triangles.
GEOMETRY
Relevant for…
Learning about the characteristics of equilateral triangles.
Definition of an equilateral triangle
As we mentioned in the introduction, an equilateral triangle is a triangle that has all sides of equal lengths. Also, the three interior angles of an equilateral triangle are also congruent and equal to 60 degrees. The following is a diagram of an equilateral triangle:
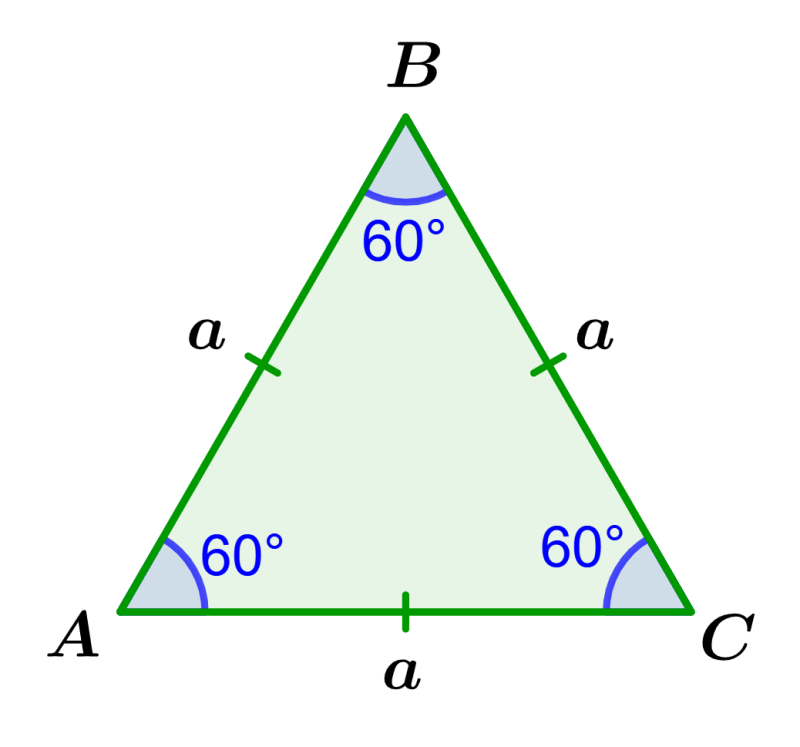
In the equilateral triangle ABC, we have the following:
$latex AB=BC=AC$
where AB, BC, and AC are the sides of the triangle. And we also have:
∠$latex A=$∠$latex B=$∠$latex C$
Important characteristics of equilateral triangles
Equilateral triangles have the following fundamental characteristics:
- An equilateral triangle has all its sides with equal length.
- All the internal sides of an equilateral triangle measure 60°.
- The equilateral triangle is a regular polygon with three sides.
- A triangle is equilateral only if the circumcenters of the three smallest triangles have the same distance from the centroid.
- A triangle is equilateral only if the three smallest triangles have the same perimeter.
- The orthocenter and centroid of the triangle are the same point.
- In an equilateral triangle, the mean, the angle bisector, and the height are all the same and are the lines of symmetry of the triangle.
Important equilateral triangle formulas
The most important formulas for equilateral triangles are the area formula and the perimeter formula.
Area of an equilateral triangle
We can calculate the area of an equilateral triangle with the following formula:
| $latex A= \frac{ \sqrt{3}}{4}{{a}^2}$ |
where a is the length of one of the sides of the triangle.
Perimeter of an equilateral triangle
We can find the perimeter of an equilateral triangle by adding the lengths of all the sides. Since all three sides are equal, we have:
| $latex p=3a$ |
where a is the length of one of the sides of the triangle.
Examples of equilateral triangle problems
EXAMPLE 1
- What is the perimeter of an equilateral triangle with sides of length 7 m?
Solution: We use the perimeter formula with $latex a=7$:
$latex p=3a$
$latex p=3(7)$
$latex p=21$
The perimeter of the triangle is 21 m.
EXAMPLE 2
- The perimeter of an equilateral triangle is 48 m. What is the length of its sides?
Solution: We start with the perimeter and we are going to find the length of its sides. Therefore, we solve for a:
$latex p=3a$
$latex 48=3a$
$latex a=16$
The length of one of the sides is 16 m.
EXAMPLE 3
- What is the area of an equilateral triangle that has sides of length 11 m?
Solution: We have $latex a=11$. Therefore, we use the formula for the area with this value :
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{11}^2})$
$latex A= \frac{ \sqrt{3}}{4}(121)$
$latex A=52.39$
The area of the equilateral triangle is 52.39 m².
EXAMPLE 4
- What is the area of an equilateral triangle that has sides of length 17 m?
Solution: We use $latex a=17$ in the area formula:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{17}^2})$
$latex A= \frac{ \sqrt{3}}{4}(289)$
$latex A=125.14$
The area of the equilateral triangle is 125.14 m².
See also
Interested in learning more about equilateral triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
