An equilateral triangle cannot have a right angle since all interior angles in an equilateral triangle measure 60°. This is because the condition for a triangle to be equilateral is that it needs to have sides with equal lengths and have angles with equal measures. We know that the interior angles in a triangle always add up to 180 °, so we can have three 60° angles that are equal.
Here, we will learn more about equilateral triangles. We will look at a definition of this type of triangle and we will learn about its most important characteristics. Also, we will look at the most used formulas and will apply them to solve some problems.
What is an equilateral triangle?
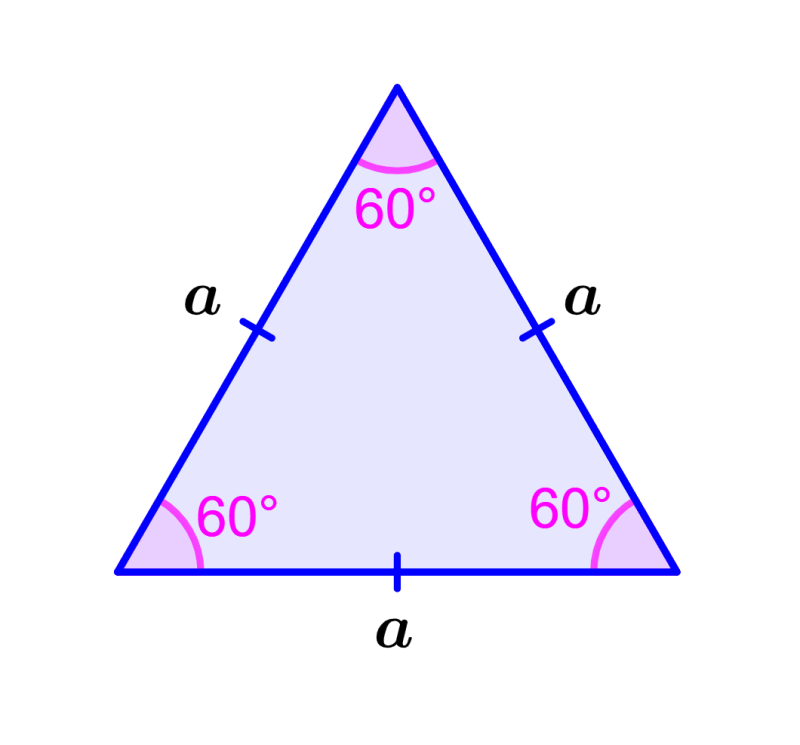
A triangle is equilateral if it has sides that are equal in length. In addition, the three interior angles must also have the same measure, that is, each interior angle must measure 60°. The following is an image of an equilateral triangle:
We can define triangle ABC. This triangle meets the following condition:
$latex AB=BC=AC$
where, AB, BC, and AC are the lengths of the sides of the triangle. And it also meets the following condition:
∠$latex A=$∠$latex B=$∠$latex C$
Properties of equilateral triangles
The following are some of the properties of equilateral triangles:
- The sides of equilateral triangles have the same length.
- Each interior angle of an equilateral triangle measures 60°.
- These triangles can be considered as regular three-sided polygons.
- The orthocenter and the centroid of an equilateral triangle are the same point.
- The mean, angle bisector, and height are all the same and are lines of symmetry of the triangle.
- For a triangle to be equilateral, the circumcenters of the three smallest triangles must have the same distance from the centroid.
- For a triangle to be equilateral, the three smallest triangles must have the same perimeter.
Formulas for equilateral triangles
The most useful formulas for solving equilateral triangle exercises are the area formula and the perimeter formula.
Area of an equilateral triangle
We use the following formula to calculate the area of an equilateral triangle:
| $latex A= \frac{\sqrt{3}}{4}{{a}^2}$ |
where a is the length of one of the sides of the triangle.
Perimeter of an equilateral triangle
We add the lengths of all the sides of the triangle to find the perimeter. In this case, those lengths are equal, so we have:
| $latex p=3a$ |
where a is the length of one of the sides of the triangle.
Examples of equilateral triangle problems
EXAMPLE 1
- Find the perimeter of an equilateral triangle that has sides of length 9 m.
Solution: We have $latex a=9$, so we use the perimeter formula with this value:
$latex p=3a$
$latex p=3(9)$
$latex p=27$
The perimeter of the triangle is 27 m.
EXAMPLE 2
- What is the length of the sides of an equilateral triangle if the perimeter is 75 m?
Solution: We can use the perimeter formula and solve for a:
$latex p=3a$
$latex 75=3a$
$latex a=25$
The length of one of the sides is 25 m.
EXAMPLE 3
- An equilateral triangle has sides of length 12 m. What is its area?
Solution: We have the length $latex a = 12$. Therefore, substituting this value in the formula for the area, we have:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{12}^2})$
$latex A= \frac{ \sqrt{3}}{4}(144)$
$latex A=63.35$
The area of the equilateral triangle is 63.35 m².
EXAMPLE 4
- If a triangle has sides of length 18 m, what is its area?
Solution: We have $latex a=18$ in the area formula:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{18}^2})$
$latex A= \frac{ \sqrt{3}}{4}(324)$
$latex A=140.3$
The area of the equilateral triangle is 140.3 m².
See also
Interested in learning more about equilateral triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
