The height of an equilateral triangle is the line segment that joins the vertex with its opposite side. The height is the perpendicular bisector of the side opposite the vertex and divides the triangle into two equal triangles with right angles. We can find a formula for the height of the equilateral triangle using the Pythagorean theorem.
In this article, we will learn everything related to the height of an equilateral triangle. We will learn how to derive its formula and apply it to solve some practice problems.
GEOMETRY
Relevant for…
Learning to find the height of an equilateral triangle with examples.
GEOMETRY
Relevant for…
Learning to find the height of an equilateral triangle with examples.
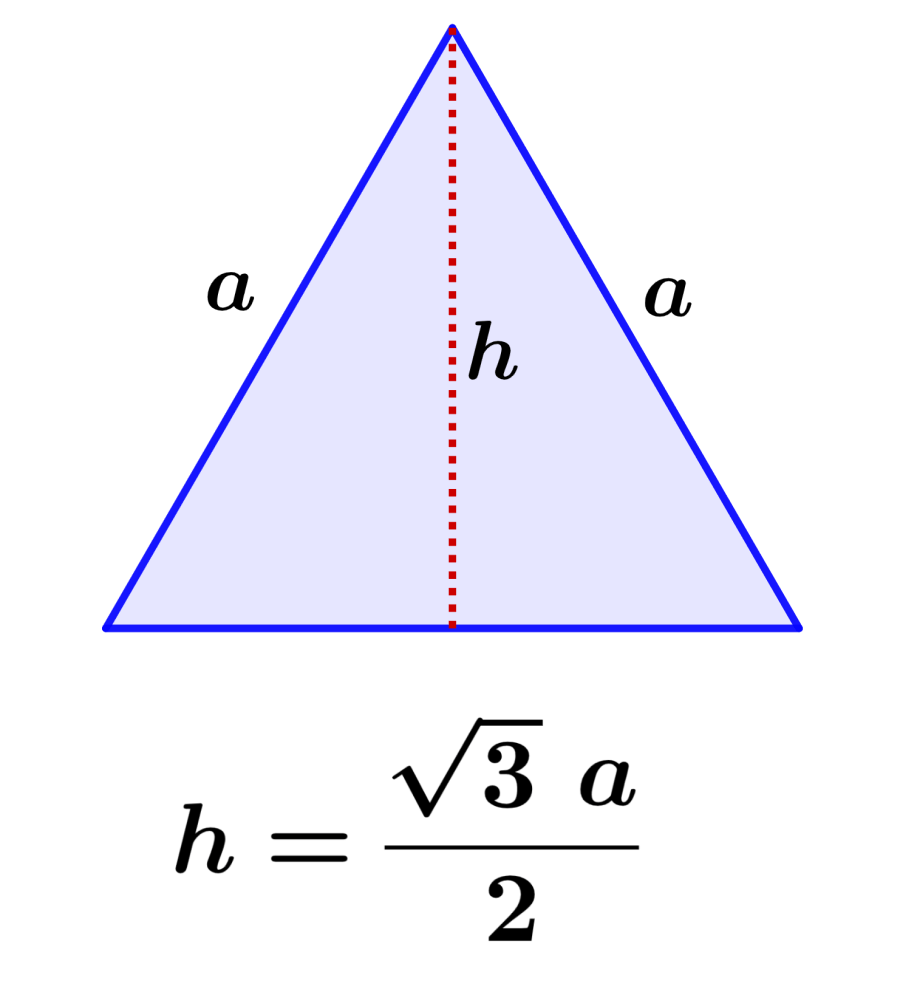
Formula for the height of an equilateral triangle
Equilateral triangles are triangles that have all of their sides with the same length. We can calculate the length of the height of equilateral triangles using the following formula:
| $$h=\frac{\sqrt{3}~a}{2}$$ |
where, a is the length of one of the sides of the equilateral triangle. Therefore, to determine the height of an equilateral triangle, we only need to know the length of one of its sides.
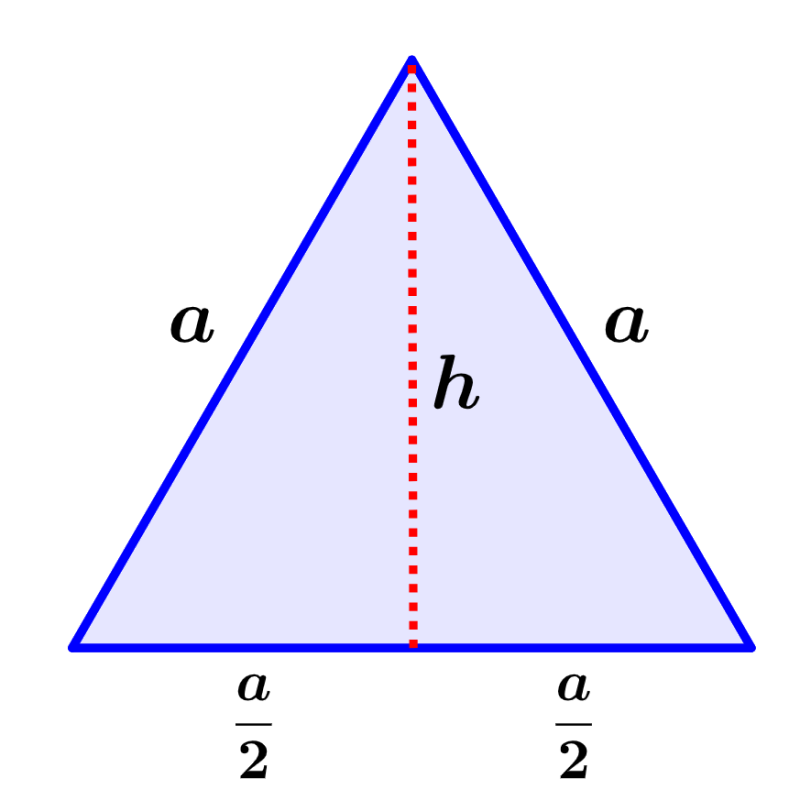
Proof of the formula for the height of an equilateral triangle
We can prove the formula for the height of an equilateral triangle using the Pythagorean theorem. Let us remember that the Pythagorean theorem tells us that the sum of the squares of the legs is equal to the square of the hypotenuse:
Hypotenuse2 = leg12+leg22
Now, we can use the following figure:
In this triangle, the sides have a length of a and the height has a length of h. We can see that the height divides the triangle into two equal right triangles.
We can use one of the right triangles to apply the Pythagorean theorem. In each triangle, the hypotenuse is equal to a, the base is equal to a/2, and the height is equal to h. Therefore, we have:
Hypotenuse2 = leg12+leg22
$$a^2 = h^2+ \left(\frac{a}{2}\right)^2$$
Now, we just have to solve this equation for the height h:
$$a^2 = h^2+ \left(\frac{a}{2}\right)^2$$
$$ h^2=a^2- \left(\frac{a^2}{4}\right)$$
$$ h^2= \frac{3a^2}{4}$$
$$ h= \frac{\sqrt{3}a}{2}$$
Therefore, we have proved the formula for the height of an equilateral triangle.
Calculate the height of an equilateral triangle with the perimeter
To find the height of an equilateral triangle using the perimeter, we have to start by determining the length of one of the triangle’s sides.
We know that equilateral triangles have all of their sides of the same length. Therefore, we can simply divide the perimeter by 3 to find the length of one side.
Finally, we apply the formula for the height of an equilateral triangle using the length found.
Alternatively, we can modify the height formula by substituting p=3a or a=p/3, where p is the perimeter and a is the length of one of the triangle’s sides. Thus, we have:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}\frac{p}{3}}{2}$$
$$ h= \frac{\sqrt{3}p}{6}$$
Calculate the height of an equilateral triangle with the area
To calculate the height of an equilateral triangle with the area, we have to use the formula for the area of an equilateral triangle to determine the length of one of its sides.
Recall that the formula for the Area of an Equilateral Triangle is:
$$ A= \frac{\sqrt{3}}{4}~a^2$$
After finding the length of one of the sides, we can simply apply the height formula.
Height of an equilateral triangle – Examples with answers
The following examples are solved using the formula for the height of an equilateral triangle. Each example has its respective solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Find the length of the height of an equilateral triangle that has sides of length 2 ft.
Solution
We are going to use the height formula to find the length we want. Substituting the value a=2, we have:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(2)}{2}$$
$latex h= \sqrt{3}$
The length of the height of the given triangle is $latex \sqrt{3}$ ft.
EXAMPLE 2
What is the height of an equilateral triangle that has sides of 5 inches?
Solution
Using the height formula with the value a=5, we have:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(5)}{2}$$
$latex h= 4.33$
The equilateral triangle has a height that measures 4.33 in.
EXAMPLE 3
If the height of an equilateral triangle is 6 inches, what is the length of one of its sides?
Solution
In this case, we have the length of the height, and we want to find the length of one of the sides of the triangle. Therefore, we use the height formula and solve for a:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ 6= \frac{\sqrt{3}a}{2}$$
$latex 12= \sqrt{3}a$
$latex a=6.928$
The length of one of the sides of the triangle is 6.928 in.
EXAMPLE 4
Determine the length of the sides of an equilateral triangle that has a height of 8 feet.
Solution
Similar to the previous problem, we can use the height formula and solve for a:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ 8= \frac{\sqrt{3}a}{2}$$
$latex 16= \sqrt{3}a$
$latex a=9.238$
The triangle has sides with a length of 9.238 ft.
EXAMPLE 5
The perimeter of an equilateral triangle is equal to 30 in. Find the length of its height.
Solution
The perimeter is the sum of the lengths of the three sides of the triangle. In an equilateral triangle, all three sides are the same length, so we can divide the perimeter by 3 to find the length of one of its sides.
Therefore, we know that the length of one of the sides of the triangle is 30/3=10. Now, we can use that length in the height formula, and we have:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(10)}{2}$$
$latex h= 8.66$
The height of the triangle is 8.66 in.
EXAMPLE 6
Determine the length of the height of an equilateral triangle that has a perimeter of 21 in.
Solution
Similar to the previous problem, we can find the length of one of the sides of the equilateral triangle if we divide its perimeter by 3.
Therefore, the sides of the triangle have a length of 18/3=6. Using this value in the height formula, we have:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(6)}{2}$$
$latex h= 5.196$
The height of the triangle is 5.196 in.
EXAMPLE 7
If the area of an equilateral triangle is equal to 60 inches squared, what is the length of its height?
Solution
To find the length of the height, we have to start by finding the length of one of the sides of the triangle. For this, we can use the formula for the area of an equilateral triangle with the given value and solve for a:
$$ A= \frac{\sqrt{3}}{4}~a^2$$
$$ 60= \frac{\sqrt{3}}{4}~a^2$$
$latex a^2= 138.564$
$latex a= 11.77$
Now, we substitute the found length in the height formula:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(11.77)}{2}$$
$$ h= 10.193$$
The height of the triangle is 10.193 in.
Height of an equilateral triangle – Practice problems
Use everything you have learned about the height of an equilateral triangle to solve the following problems. Select your answer and click “Check” to see if it is the correct solution.
See also
Interested in learning more about equilateral triangles? You can visit these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
