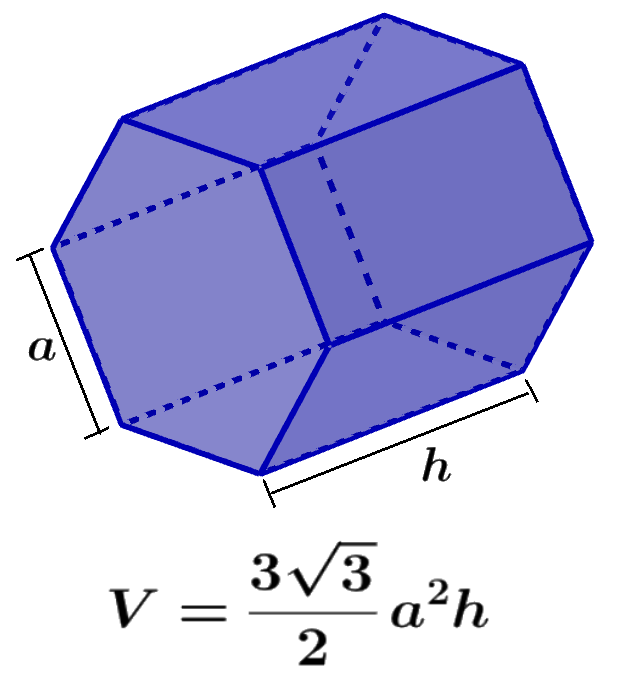
The volume of a hexagonal prism is calculated by multiplying the area of the hexagonal base by the height of the prism. On the other hand, the surface area of the hexagonal prism is calculated by adding the areas of all its faces.
Here, we will look at the formulas that we can use to calculate the surface area and the volume of hexagonal prisms. Also, we will use these formulas to solve some practice problems.
How to find the volume of a hexagonal prism
The volume of a hexagonal prism is calculated by multiplying the area of the base by the height of the prism. These polyhedra have hexagonal bases, so we have to calculate the area of a hexagon to find the volume. Recall that the following is the formula for the area of a hexagon:
$latex A=\frac{3\sqrt{3}}{2}{{a}^2}$
where a is the length of one of the sides of the hexagon.
This formula can be derived by dividing the hexagon into six congruent triangles and finding the area of one of the triangles.
Since we have a formula for the area of the base of the rectangular prism, the formula for its volume is:
| $latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$ |
where a is the length of one of the sides of the hexagonal base and h is the length of the height of the prism.
How to find the surface area of a hexagonal prism
To find the surface area of a hexagonal prism, we have to add up the areas of all its faces.
Hexagonal prisms have two hexagonal faces that are parallel and congruent. These prisms also have six lateral rectangular faces that are also congruent.
The area of a regular hexagon can be found using the formula: $latex A=\frac{3 \sqrt{3}}{2}{{a}^2}$, where, a is the length of one of the sides of the hexagon. This means that the area of both hexagonal faces is $latex A=3 \sqrt{3}{{a}^2}$.
The area of one of the rectangular faces of the prism is equal to ah, where a is the length of one of the sides of the hexagon and h is the height of the prism. Therefore, the area of the six rectangular faces equals 6ah.
By adding the expressions obtained for the areas, we have:
| $latex A_{S}=3\sqrt{3}{{a}^2}+6ah$ |
Area and volume of a hexagonal prism – Examples with answers
EXAMPLE 1
What is the volume of a hexagonal prism that has sides of length 4 m and height 6 m?
Solution
We have the following information:
- Sides of the hexagon, $latex a=4$
- Height, $latex h=6$
Using the volume formula, we have:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(4)}^2}(6)$
$latex V=\frac{3\sqrt{3}}{2}(16)(6)$
$latex V=249.4$
The volume is 249.4 m³.
EXAMPLE 2
What is the surface area of a hexagonal prism that has a hexagonal base with sides of length 4 m and a height of 6 m?
Solution
We have the following values:
- Hexagon sides, $latex a=4$
- Prism height, $latex h=6$
Using the formula for the surface area with these values, we have:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex A_{S}=3\sqrt{3}{{(4)}^2}+6(4)(6)$
$latex A_{S}=3\sqrt{3}(16)+144$
$latex A_{S}=83.14+90$
$latex A_{S}=173.14$
The surface area is 173.14 m².
EXAMPLE 3
A hexagonal prism has sides of length 5 m and a height of 5 m. What is its volume?
Solution
From the question, we have the following values:
- Sides of the hexagon, $latex a=5$
- Height, $latex h=5$
Substituting these values in the volume formula, we have:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(5)}^2}(5)$
$latex V=\frac{3\sqrt{3}}{2}(16)(6)$
$latex V=324.8$
The volume is 324.8 m³.
EXAMPLE 4
We have a prism with a height of 10 m and a hexagonal base with sides with a length of 5 m. What is its surface area?
Solution
We acknowledge the following:
- Hexagon sides, $latex a=5$
- Prism height, $latex h=10$
Using the formula for surface area with these values, we have:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex A_{S}=3\sqrt{3}{{(5)}^2}+6(5)(10)$
$latex A_{S}=3\sqrt{3}(25)+300$
$latex A_{S}=129.9+300$
$latex A_{S}=429.9$
The surface area is 429.9 m².
EXAMPLE 5
What is the volume of a hexagonal prism that has sides of length 7 m and a height of 8 m?
Solution
We have the following information:
- Sides of the hexagon, $latex a=7$
- Height, $latex h=8$
We use this information in the volume formula:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(7)}^2}(8)$
$latex V=\frac{3\sqrt{3}}{2}(49)(8)$
$latex V=1018.4$
The volume is 1018.4 m³.
EXAMPLE 6
What is the height of a prism that has a surface area of 226.77 m² and a hexagonal base with sides of length 3 m?
Solution
We have the following values:
- Hexagon sides, $latex a=3$
- Surface area, $latex A = 226.77$
In this case, we have the surface area and we want to find the length of the height of the prism. Therefore, we use the values given in the formula and solve for h:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex 226.77=3\sqrt{3}{{(3)}^2}+6(3)h$
$latex 226.77=46.77+18h$
$latex 18h=226.77-46.77$
$latex 18h=180$
$latex h=10$
The length of the height is equal to 10 m.
EXAMPLE 7
A prism has a hexagonal base with sides that are 8 m long and 9 m in height. What is its volume?
Solution
We have the following values:
- Sides of the hexagon, $latex a=8$
- Height, $latex h=9$
Using the volume formula, we have:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(8)}^2}(9)$
$latex V=\frac{3\sqrt{3}}{2}(64)(9)$
$latex V=1496.5$
The volume is 1496.5 m³.
EXAMPLE 8
If a prism has a surface area of 542.6 m² and the hexagonal base has sides of length 6 m, what is the length of its height?
Solution
We have the following:
- Hexagon sides, $latex a=6$
- Surface area, $latex A=542.6$
We use the formula for surface area with the given values and solve for h:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex 542.6=3\sqrt{3}{{(6)}^2}+6(6)h$
$latex 542.6=254.6+36h$
$latex 36h=542.6-254.6$
$latex 36h=288$
$latex h=8$
The length of the height is equal to 8 m.
Area and volume of a hexagonal prism – Practice problems
If a hexagonal prism has a surface area of 475 m2 and its base has sides of length 6 m, what is the length of its height?
Write the answer in the input box.
See also
Interested in learning more about hexagonal prisms? Take a look at these pages: