A hexagonal prism is a prism that has hexagon-shaped bases that are parallel to each other. The hexagonal bases are joined by six rectangular side faces. Hexagonal prisms have a total of 8 faces, 12 vertices, and 18 edges. If the prism is regular, the sides of the hexagonal faces are equal and all the lateral faces are also equal. Each vertex is connected by three edges.
Here, we will learn more about the faces, vertices, and edges of these prisms. We will use diagrams to illustrate the concepts and improve understanding.
Faces found in a hexagonal prism
The faces are the flat surfaces of the hexagonal prism. These prisms are composed of two hexagonal faces that are parallel to each other. These hexagonal faces are called the bases of the prism. The bases are joined by six lateral rectangular faces.
If the prism is regular, the six side faces are congruent. An important characteristic of regular hexagonal prisms is that the lateral rectangular faces intersect the hexagonal faces at an angle of 90 degrees.
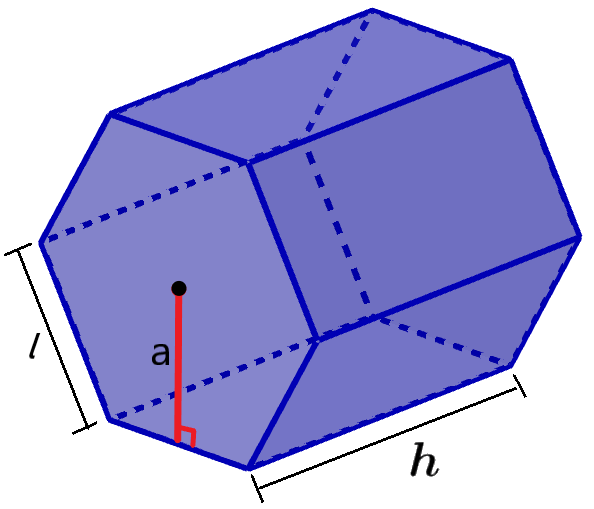
We can calculate the surface area of the prism by adding the areas of all the faces. The area of both hexagonal faces is equal to 6al, where a is the length of the apothem and l is the length of one of the sides of the hexagonal base.
Also, the area of the rectangular faces is 6lh, where l is the length of the sides of the base and h is the length of the height of the prism. This means that the total surface area of the hexagonal prism is equal to 6al + 6lh.
Vertices found in a hexagonal prism
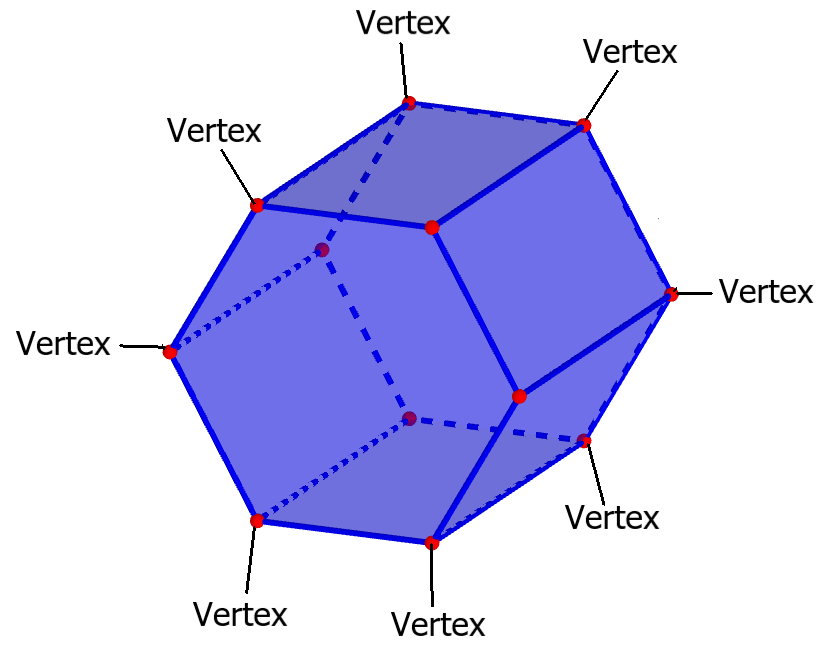
The vertices of a hexagonal prism are the points where three edges meet. Vertices are generally points where two or more line segments meet. Therefore, we can determine that we have 12 vertices in a hexagonal prism.
Another way to define vertices is as the points where three faces, one hexagonal and two rectangular, meet.
Edges found in a hexagonal prism
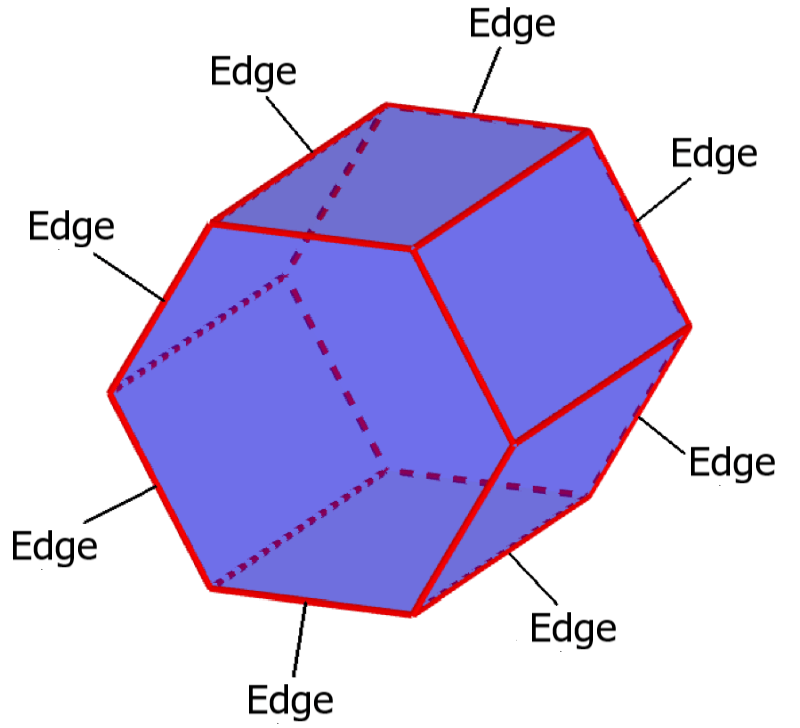
The edges of a hexagonal prism are the line segments that bound the prism. In general, an edge is a line segment that joins two vertices of a polyhedron or other geometric figure. We can also define the edges as the segments where two faces of the prism meet.
We can determine that we have a total of 18 edges in a hexagonal prism.
See also
Interested in learning more about hexagonal prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
