Hexagonal prisms are three-dimensional figures, which are formed by two parallel hexagonal bases. These bases are connected by six lateral rectangular faces. This means that in total, a hexagonal prism has 8 faces, two hexagonal and six rectangular. Since these figures are three-dimensional, they have two important properties, volume and surface area.
Here, we will learn about some of the most important characteristics of a prism. Also, we will learn about the most used formulas of these prisms and we will use them to solve some problems.
Definition of a hexagonal prism
A hexagonal prism is a 3D figure that has two hexagonal bases that are parallel to each other. These hexagonal bases are joined by six lateral rectangular faces. Hexagonal prisms have a total of 8 faces, 12 vertices, and 18 edges.
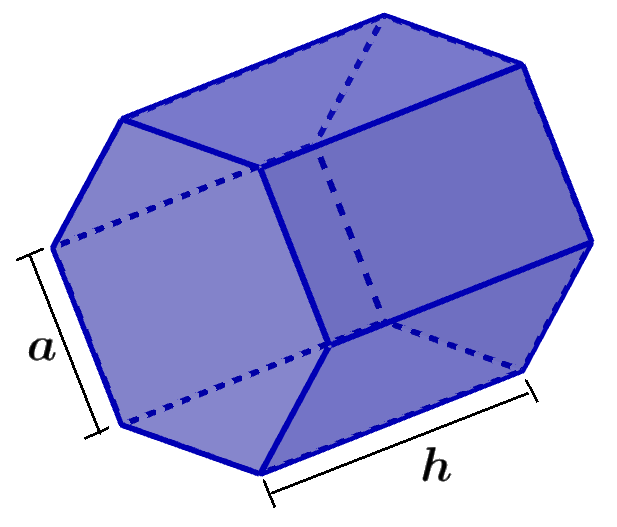
Hexagonal prisms can be regular or irregular. A regular hexagonal prism is a prism in which its bases are regular hexagons. Regular hexagons have all their sides of the same length. These are the most common hexagonal prisms.
On the other hand, irregular hexagonal prisms are prisms in which their bases are irregular hexagons. Irregular hexagons have sides with different lengths and internal angles with different measurements.
Fundamental characteristics of a hexagonal prism
The following are the main characteristics of a hexagonal prism:
- Both bases are hexagons.
- The bases are parallel to each other.
- If the prism is regular, both hexagonal faces are congruent and have sides of the same length.
- If the prism is regular, the six lateral faces are congruent rectangles.
- In total, these prisms have 8 faces: 2 hexagonal and 6 rectangular.
- These prisms have 12 vertices.
- These prisms have 18 edges.
Important hexagonal prism formulas
Since hexagonal prisms are 3D figures, their most important formulas are the volume formula and the surface area formula.
Formula for the volume of a hexagonal prism
The volume of a hexagonal prism is equal to the area of its base multiplied by the height of the prism. Therefore, we have the following:
| $latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$ |
where a represents the length of one of the sides of the hexagon and h represents the height of the prism.
Formula for the surface area of a hexagonal prism
The surface area is calculated by adding the areas of all the faces of the hexagon. We have two hexagonal faces and two rectangular faces. The area of both rectangular faces is equal to $latex 3 \sqrt{3}{{a}^2}$ and the area of the six rectangular faces is equal to 6ah. Therefore, we have:
| $latex A_{s}=3\sqrt{3}{{a}^2}+6ah$ |
Examples of hexagonal prism problems
The formulas seen above are applied to solve the following exercises.
EXAMPLE 1
A hexagonal prism has a height of 10 m and its base has sides of length 5 m. What is its volume?
Solution: We have the lengths $latex h=10$ and $latex a=5$. We use the volume formula with these values, and we have:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(5)}^2}(10)$
$latex V=\frac{3\sqrt{3}}{2}(25)(10)$
$latex V=649.5$
The volume is 649.5 m³.
EXAMPLE 2
What is the volume of a prism that has a height of 12 m and a hexagonal base with sides of length 4 m?
Solution: We use the volume formula with the given values:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(4)}^2}(12)$
$latex V=\frac{3\sqrt{3}}{2}(16)(10)$
$latex V=415.7$
The volume is 415.7 m³.
EXAMPLE 3
What is the surface area of a hexagonal prism that has a height of 8 m and sides of length 4 m?
Solution: We use the formula for surface area with the given values:
$latex A_{s}=3\sqrt{3}{{a}^2}+6ha$
$latex A_{s}=3\sqrt{3}{{(4)}^2}+6(8)(4)$
$latex A_{s}=83.1+192$
$latex A_{s}=275.1$
The surface area is 275.1 m².
EXAMPLE 4
A hexagonal prism has a height of 11 m and sides of length 6 m. What is its surface area?
Solution: Using the formula for surface area, we have:
$latex A_{s}=3\sqrt{3}{{a}^2}+6ha$
$latex A_{s}=3\sqrt{3}{{(6)}^2}+6(12)(6)$
$latex A_{s}=187.1+432$
$latex A_{s}=619.1$
The surface area is 619.1 m².
See also
Interested in learning more about hexagonal prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
