Vertical angles are formed at the intersection of two lines. The vertical angles theorem tells us that the vertical angles formed at an intersection are equal. Also, a vertical angle and its adjacent angle are supplementary angles since they add up to 180 degrees.
In this article, we will look at a summary of the vertical angles theorem. Then, we will apply this theorem by solving various practice problems.
Summary of the vertical angles theorem
Vertical angles are the angles formed by the intersection of two lines. For example, in the diagram below, we have two pairs of vertical angles.
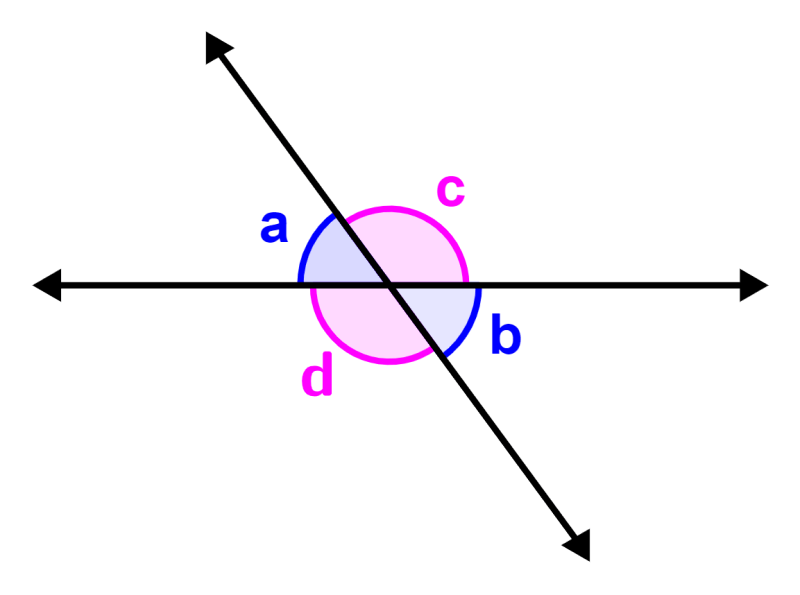
Angles a and b and angles c and d are pairs of vertical angles.
The vertical angles theorem tells us that pairs of vertical angles have the same size. Therefore, in the diagram shown above, we know that angles a and b and angles c and d are equal.
Proof of the vertical angles theorem
In the following diagram, we can see lines AB and CD, which intersect at point O. The intersection of lines forms two pairs of vertical angles:
- ∠1 and ∠2 (blue angles)
- ∠3 and ∠4 (pink angles)
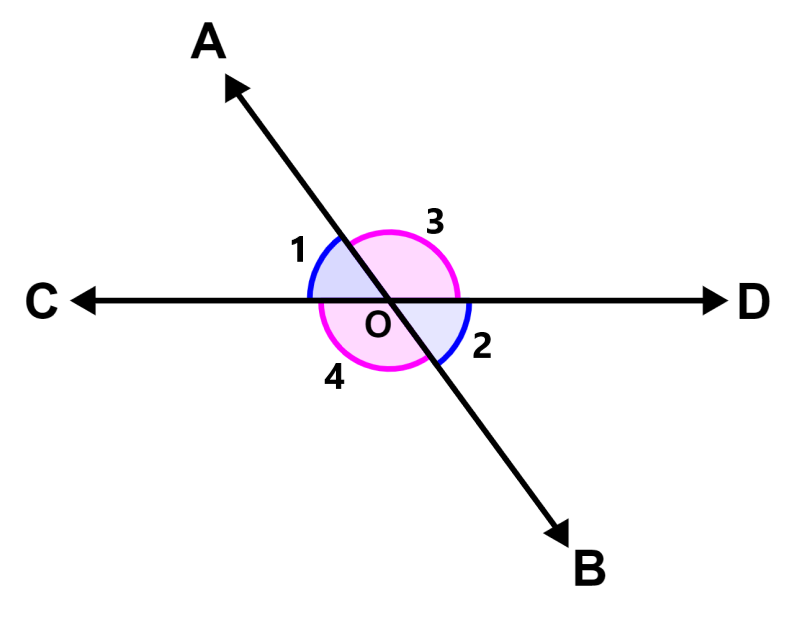
In the diagram, we see that ray OA is located on line CD. Therefore, we can use the axiom of linear pairs, which tells us that if a ray is located on a line, the adjacent angles form a linear pair of angles. That is, we know that the angles that form a straight line must add up to 180°. So, we have:
∠1 + ∠3 = 180° (linear pair)
Similarly, we also have:
∠3 + ∠2 = 180° (linear pair)
Since both equations are equal to 180°, we can combine them to obtain:
∠1 + ∠3 = ∠3 + ∠2
∠1 = ∠2
This means that the vertical angles ∠1 and ∠2 are equal. Therefore, we have proved the vertical angles
Vertical angles theorem – Examples with answers
EXAMPLE 1
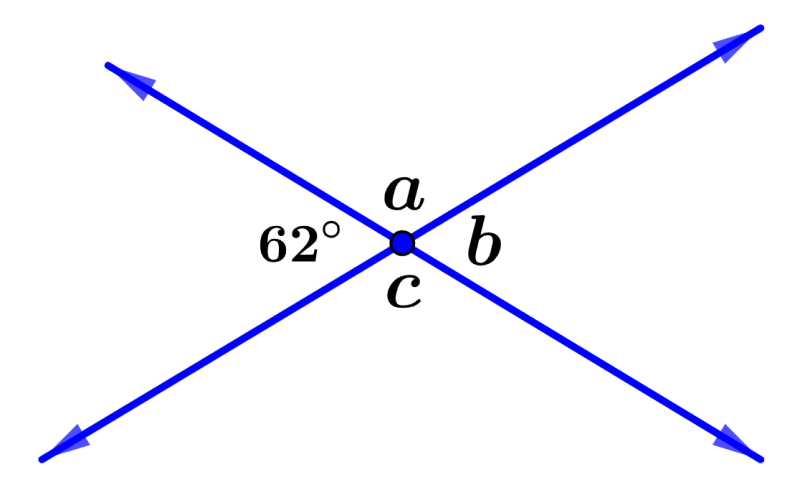
Determine the size of each of the angles in the diagram below.
Solution
Angles ∠62° and ∠b are a pair of vertical angles. Thus, we have:
∠b = 62°
The value of ∠a can be found considering that it is a supplementary angle to the angle of 62°. That is, these angles add up to 180° and we have:
62° + ∠a = 180°
∠a = 118°
Finally, we can see that angles ∠a and ∠c are another pair of vertical angles, so we have:
∠c = 118°
EXAMPLE 2
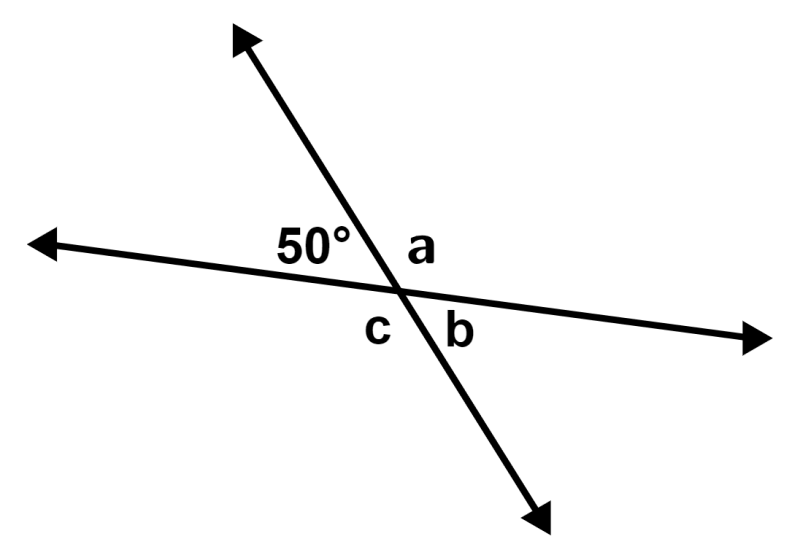
Determine the sizes of angles a, b, and c in the following diagram:
Solution
We see that the angles ∠50 ° and ∠b are a pair of vertical angles, so we have:
∠b = 50°
Now, we can find the value of ∠a by considering that it is a supplementary angle to the angle ∠50 °, so we have:
50° + ∠a = 180°
∠a = 130°
The angles ∠a and ∠c are another pair of vertical angles, so we have:
∠c = 130°
EXAMPLE 3
What is the value of Y in the diagram below?
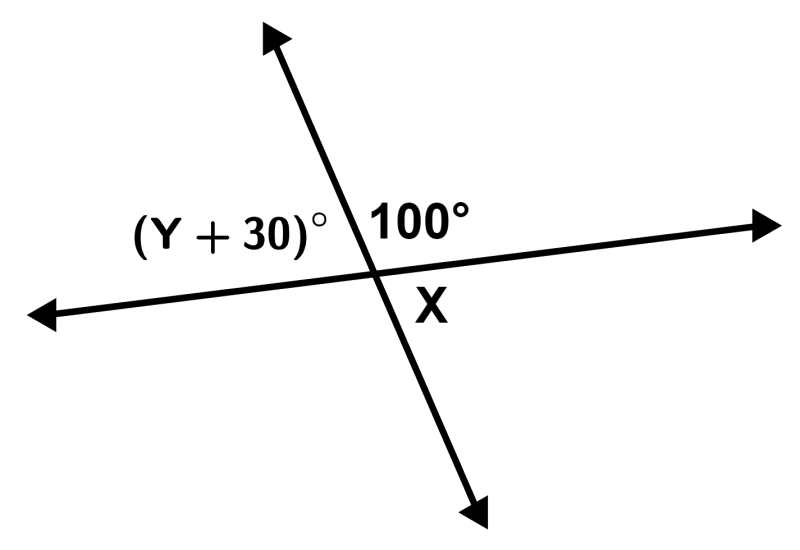
Solution
Angles ∠100° and ∠X are part of a straight line, so they are supplementary. Therefore, we have:
100° + ∠X = 180°
∠X = 80°
Since the angles (Y + 30)° and X are vertical angles, we can form the following equation and solve for Y:
Y + 30 = 80
Y = 50°
EXAMPLE 4
What is the value of Z in the diagram below?
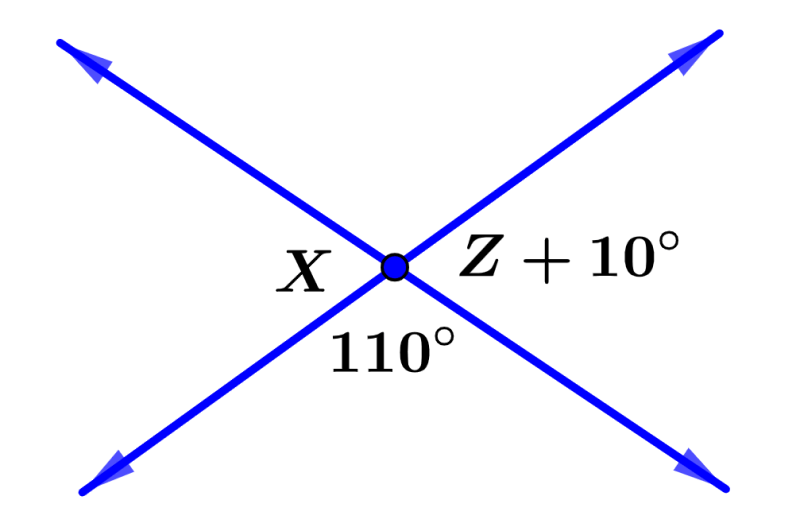
Solution
This problem is similar to the previous one. Therefore, we know that angles ∠X and ∠110° form a straight line, so they are supplementary. Then, we have:
110° + ∠X = 180°
∠X = 70°
We also know that angles (Z + 10)° and X are opposite verticals, so we have:
Z + 10 = 70
Z = 60°
EXAMPLE 5
We have that the angles (4x-15)° and (3x+22)° are opposite vertical angles. Determine the value of x and the size of the given angles.
Solution
The opposite vertical angles are equal, so we have:
4x-15 = 3x + 22
4x-3x = 22 + 15
x = 37
The value of the given angles is:
4(37)-15 = 133°
EXAMPLE 6
We have the angles (5x-11)° and (3x+23)°, which are opposite vertical angles. Determine the value of x and the size of the given angles.
Solution
Opposite vertical angles are equal, so we have:
5x-11 = 3x + 23
5x-3x = 23 + 11
2x = 34
x = 17
The value of the given angles is:
3(17)+23 = 74°
Vertical angles theorem – Practice problems
See also
Interested in learning more about vertical angles and other types of angles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
