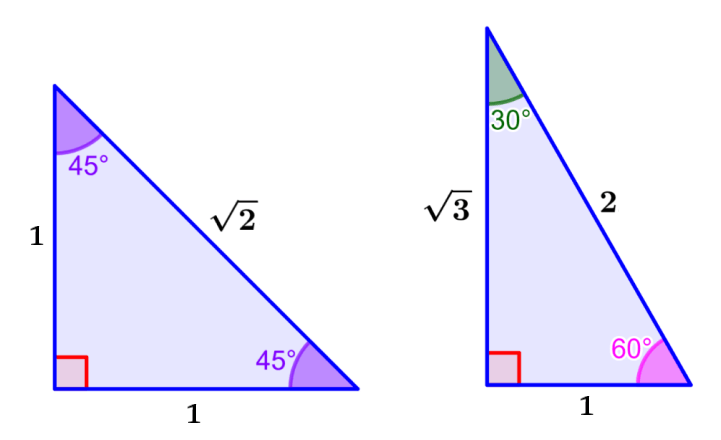
Special angles are angles that have values that are common in trigonometry exercises and in everyday life in general. Generally, the special angles are considered to be the angles of 30°, 45°, and 60°. These angles have trigonometric ratios that are easy to remember.
Here, we will learn about the trigonometric ratios of the special angles 30°, 45°, and 60°. Also, we will learn how to derive these trigonometric ratios.
Trigonometric ratios of 45°
To find the trigonometric ratios of a 45° angle, we can consider the following isosceles right triangle:
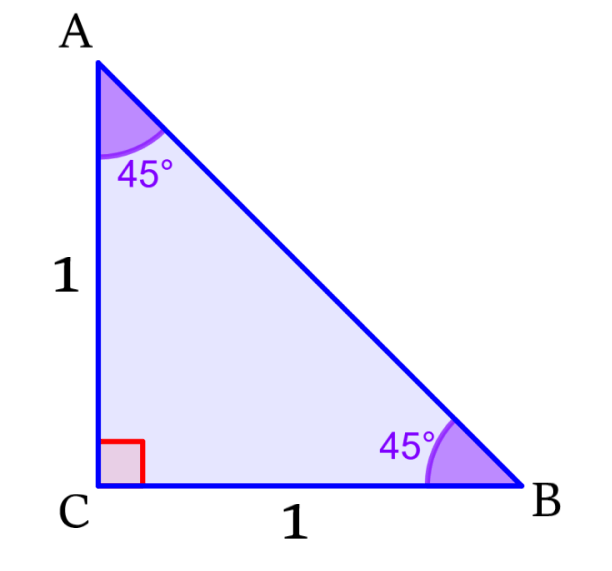
This triangle has two angles with the same measures, so both of its legs have the same length of 1 unit.
We can use the Pythagorean theorem to find the length of the hypotenuse:
$latex {{AB}^2}={{BC}^2}+{{AC}^2}$
$latex {{AB}^2}={{1}^2}+{{1}^2}$
$latex {{AB}^2}=2$
$latex AB=\sqrt{2}$
Now, we can use the same triangle to obtain the values of the trigonometric ratios, sine, cosine, and tangent:
Using the definition of sine (opposite side over hypotenuse), we have:
$$\sin(45^{\circ})=\frac{AC}{AB}=\frac{1}{\sqrt{2}}$$
Using the definition of cosine (adjacent side over hypotenuse), we have:
$$\cos(45^{\circ})=\frac{BC}{AB}=\frac{1}{\sqrt{2}}$$
Using the definition of the tangent (opposite side over adjacent side), we have:
$$\tan(45^{\circ})=\frac{AC}{BC}=1$$
In short, we have the following:
| $$\sin(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\cos(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\tan(45^{\circ})=1$$ |
Trigonometric ratios of 30°
To find the trigonometric ratios of the 30° angle, we are going to use an equilateral triangle that has side lengths of 2 units.
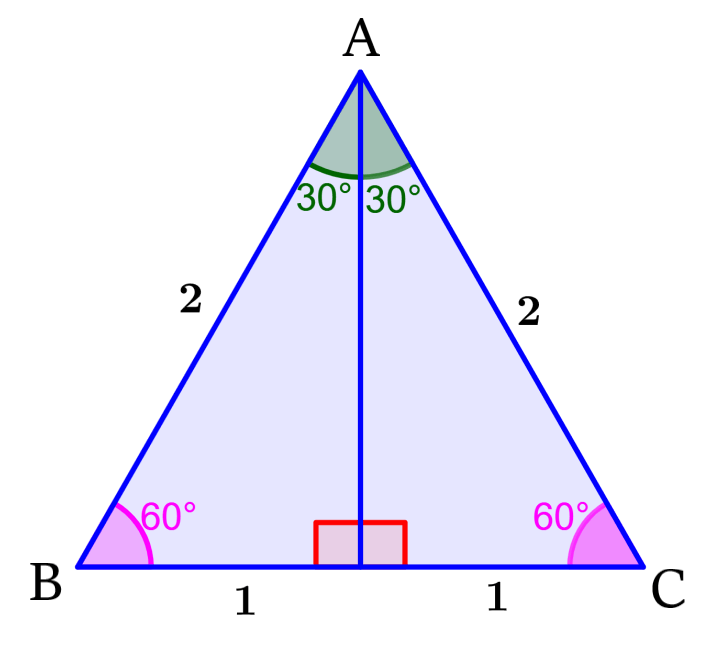
D is the point where the perpendicular segment from A meets the base. The segment AD divides the equilateral triangle into two equal triangles that have the angles 30°, 60° and 90°.
We can find the length of segment AD using the Pythagorean theorem:
$latex {{AD}^2}+{{BD}^2}={{AB}^2}$
$latex {{AD}^2}+{{1}^2}={{2}^2}$
$latex {{AD}^2}+1=4$
$latex {{AD}^2}=3$
$latex AD=\sqrt{3}$
Using the definition of sine (opposite side over hypotenuse), we have:
$$\sin(30^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Using the definition of cosine (adjacent side over hypotenuse), we have:
$$\cos(30^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Using the definition of the tangent (opposite side over adjacent side), we have:
$$\tan(30^{\circ})=\frac{BD}{AD}=\frac{1}{\sqrt{3}}$$
In short, we have the following:
| $$\sin(30^{\circ})=\frac{1}{2}$$ $$\cos(30^{\circ})=\frac{\sqrt{3}}{2}$$ $$\tan(30^{\circ})=\frac{1}{\sqrt{3}}$$ |
Trigonometric ratios of 60°
We can find the trigonometric ratios of the 60° angle using the same triangle that we used to find the trigonometric ratios of 30°.

Therefore, we use the lengths $latex AB=2$, $latex BD=1$, and $latex AD=\sqrt{3}$ with the trigonometric functions sine, cosine, and tangent.
Using the definition of sine (opposite side over hypotenuse), we have:
$$\sin(60^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Using the definition of cosine (adjacent side over hypotenuse), we have:
$$\cos(60^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Using the definition of the tangent (opposite side over adjacent side), we have:
$$\tan(60^{\circ})=\frac{AD}{BD}=\sqrt{3}$$
In short, we have the following:
| $$\sin(60^{\circ})=\frac{\sqrt{3}}{2}$$ $$\cos(60^{\circ})=\frac{1}{2}$$ $$\tan(60^{\circ})=\sqrt{3}$$ |
Table of the trigonometric ratios of special angles
The trigonometric ratios of the angles 30°, 45° and 60° are summarized in the following table:
| Ratio | θ = 30° | θ = 30° | θ = 30° |
| sin θ | $latex \frac{1}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{\sqrt{3}}{2}$ |
| cos θ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{1}{2}$ |
| tan θ | $latex \frac{1}{\sqrt{3}}$ | 1 | $latex \sqrt{3}$ |
It is a good idea to memorize these trigonometric ratios since several problems found in trigonometry use the 30°, 45°, and 60° angles.
See also
Interested in learning more about special angles and triangles? Look at these pages: