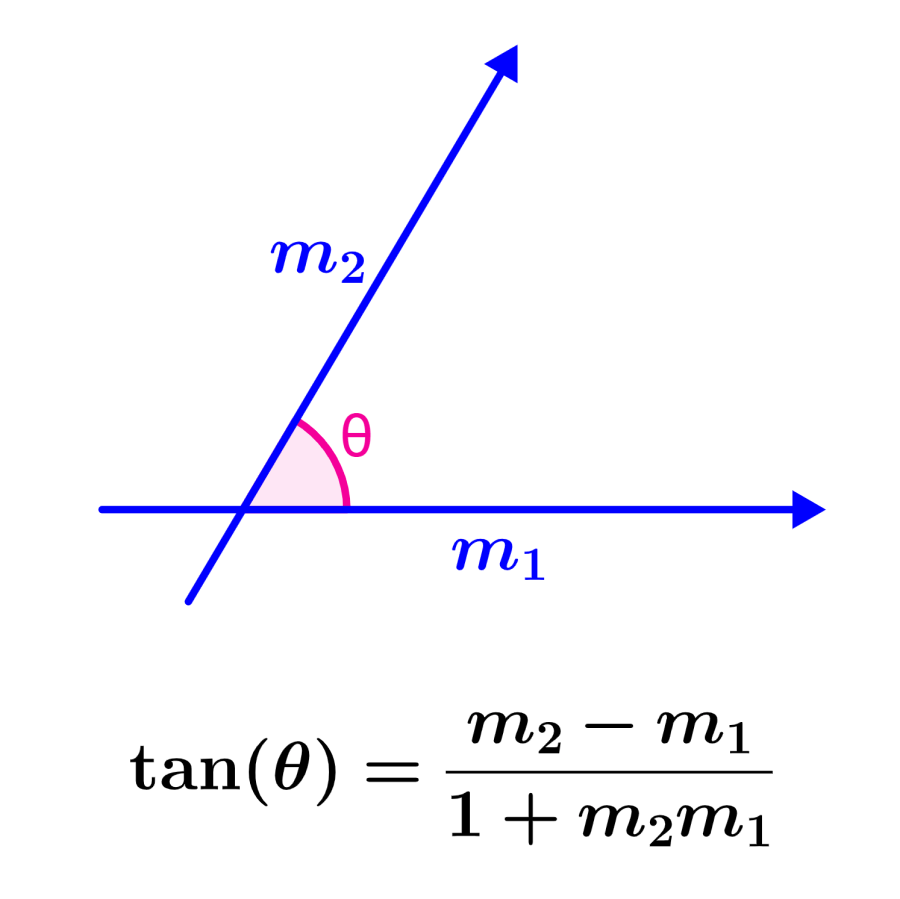The angle between two lines allows us to determine the inclination that exists between the lines. We can calculate the angle between two straight lines using a general formula that uses the slopes of both lines. This formula can be derived using trigonometry.
Here, we’ll learn how to use the slopes of two lines to find the angle between them. We will use the general formula to solve some practice problems.
Formula for the angle between two lines
If we have the two lines $latex y=m_{1}x+c_{1}$ and $latex y=m_{2}x+c_{2}$, the angle between the lines is given by the following formula:
| $$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$ |
where, θ is the angle between the lines, $latex m_{1}$ is the slope of the first line and $latex m_{2}$ is the slope of the second line as shown in the following diagram:
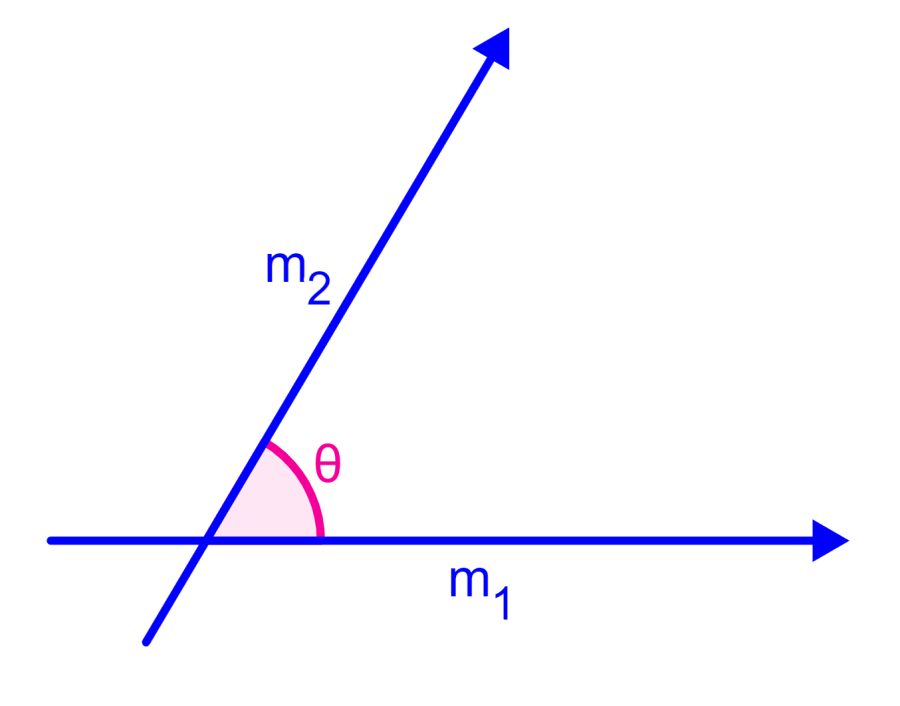
You can choose the slopes in any order. Therefore, $latex m_{2}$ can be greater than or less than $latex m_{1}$.
Proof for the formula of the angle between two lines
To prove the formula for the angle between two lines, we are going to use trigonometry along with the following diagram:
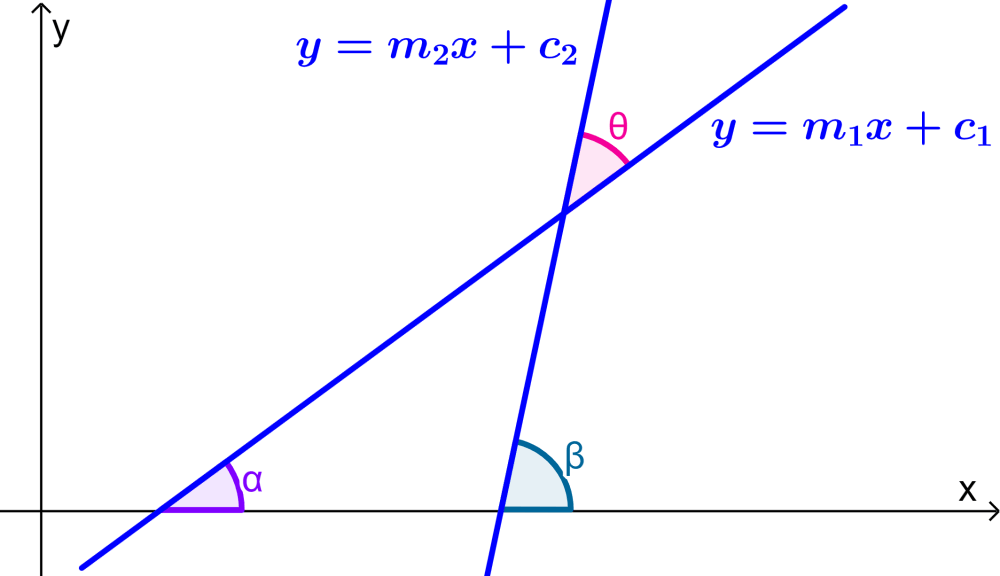
Here, we have the lines $latex y=m_{1}x+c_{1}$ and $latex y=m_{2}x+c_{2}$, which form the angles α and β with the x-axis respectively.
Using angle theorems, we can determine that $latex \theta = \beta – \alpha$. Therefore, we have the following:
$latex \tan(\theta)=\tan(\beta -\alpha)$
Using the Sum and Difference Identities formula for the tangent, we have:
$$\tan(\theta)=\frac{\tan(\beta)-\tan(\alpha)}{1+\tan(\beta)\tan(\alpha)}$$
Now, we can write $latex \tan(\beta)=m_{2}$ and $latex \tan(\alpha)=m_{1}$, since these are the slopes of the lines. Therefore, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
Angle between two lines – Examples with answers
The following examples are solved using the formula for the angle between two lines. Each example has its respective solution, but try to solve the problems before looking at the answer.
EXAMPLE 1
Find the angle between the lines $latex y=x$ and $latex y=3x-4$.
Solution
Recall that in the form $latex y=mx+b$, m is the slope of the line. Therefore, we have:
- The line $latex y=x$ has a slope of 1, so $latex m_{1}=1$
- The line $latex y=3x-4$ has a slope of 3, so $latex m_{2}=3$
Using the formula for the angle between two lines, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{3-1}{1+(3)(1)}$$
$$\tan(\theta)=\frac{2}{4}$$
$$\tan(\theta)=\frac{1}{2}$$
$$\theta=\tan^{-1}\left(\frac{1}{2}\right)$$
$$\theta=26.6^{\circ}$$
EXAMPLE 2
What is the angle between the lines $latex y=2x-5$ and $latex y=5x+6$?
Solution
We have the following:
- The line $latex y=2x-5$ has a slope of 2, so $latex m_{1}=2$
- The line $latex y=5x+6$ has a slope of 5, so $latex m_{2}=5$
Applying the formula for the angle between two lines, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{5-2}{1+(5)(2)}$$
$$\tan(\theta)=\frac{3}{11}$$
$$\theta=\tan^{-1}\left(\frac{3}{11}\right)$$
$$\theta=15.26^{\circ}$$
EXAMPLE 3
Find the angle between the lines $latex y=3+x$ and $latex y=6+2x$.
Solution
We can obtain the following information:
- The line $latex y=3+x$ has a slope of 1, so $latex m_{1}=1$
- The line $latex y=6+2x$ has a slope of 2, so $latex m_{2}=2$
Using the formula for the angle between two lines, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{2-1}{1+(2)(1)}$$
$$\tan(\theta)=\frac{1}{3}$$
$$\theta=\tan^{-1}\left(\frac{1}{3}\right)$$
$$\theta=18.43^{\circ}$$
EXAMPLE 4
Determine the angle between the lines $latex y=6x-7$ and $latex y=2-x$.
Solution
We have the following:
- The line $latex y=6x-7$ has a slope of 6, so $latex m_{1}=6$
- The line $latex y=2-x$ has a slope of -1, so $latex m_{2}=-1$
Using the formula with these values, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-1-6}{1+(-1)(6)}$$
$$\tan(\theta)=\frac{-7}{-5}$$
$$\tan(\theta)=\frac{7}{5}$$
$$\theta=\tan^{-1}\left(\frac{7}{5}\right)$$
$$\theta=54.46^{\circ}$$
EXAMPLE 5
What is the angle between the lines $latex y=2x+3$ and $latex y=5-2x$.
Solution
We can obtain the following information:
- The line $latex y=2x+3$ has a slope of 2, so $latex m_{1}=2$
- The line $latex y=5-2x$ has a slope of -2, so $latex m_{2}=-2$
Applying the formula with these values, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2-2}{1+(-2)(2)}$$
$$\tan(\theta)=\frac{-4}{-3}$$
$$\theta=\tan^{-1}\left(\frac{4}{3}\right)$$
$$\theta=53.13^{\circ}$$
EXAMPLE 6
Find the angle between the lines $latex y=4-2x$ and $latex y=9-3x$.
Solution
We have the following:
- The line $latex y=4-2x$ has a slope of -2, so $latex m_{1}=-2$
- The line $latex y=9-3x$ has a slope of -3, so $latex m_{2}=-3$
Using the formula for the angle between two lines, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-3-(-2)}{1+(-3)(-2)}$$
$$\tan(\theta)=\frac{-1}{7}$$
$$\theta=\tan^{-1}\left(-\frac{1}{7}\right)$$
$$\theta=8.13^{\circ}$$
EXAMPLE 7
Find the angle between the lines $latex y=4$ and $latex 3y+2x-6=0$.
Solution
We have the following:
- The line $latex y=4$ is horizontal and has a slope of 0, so $latex m_{1}=0$
- The line $latex 3y+2x-6=0$ can be written as $latex y=-2/3x+2$, so it has a slope of -2/3, $latex m_{2}=-2/3$
Using the formula for the angle between two lines, we have:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2/3}{1+(-2/3)(0)}$$
$$\tan(\theta)=\frac{-2/3}{1}$$
$$\tan(\theta)=-\frac{2}{3}$$
$$\theta=\tan^{-1}\left(-\frac{2}{3}\right)$$
$$\theta=33.69^{\circ}$$
Angle between two lines – Practice problems
Apply the formula for the angle between two lines to solve the following problems. If you have trouble with this, you can use the solved examples above as a guide.
See also
Interested in learning more about equations of lines? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
