There are different types of angles in nature and each of them has a relevant importance in different aspects of our daily life. For example, engineers use angles when designing machines, roads, and bridges. Angles are even used in sports.
In this article, we will look at the most important types of angles that we can find. We will see angles that are classified with respect to their magnitude, as well as angles that are classified with respect to their rotation. We will use diagrams to visualize each type of angle.
Types of angles based on their magnitude
There are seven types of angles based on their magnitude. These are:
- Null angle
- Acute angles
- Right angles
- Obtuse angles
- Straight angle
- Oblique angle
- Full angle
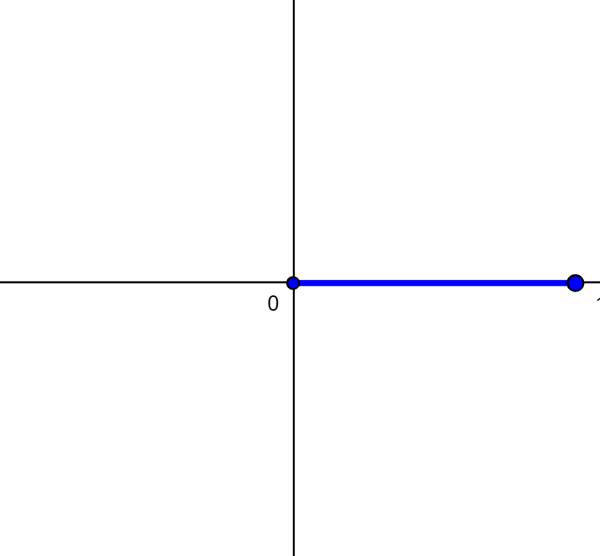
Null angle
A null angle is an angle that has zero degrees (0°). This angle is formed when both lines of the angle are in the same position.
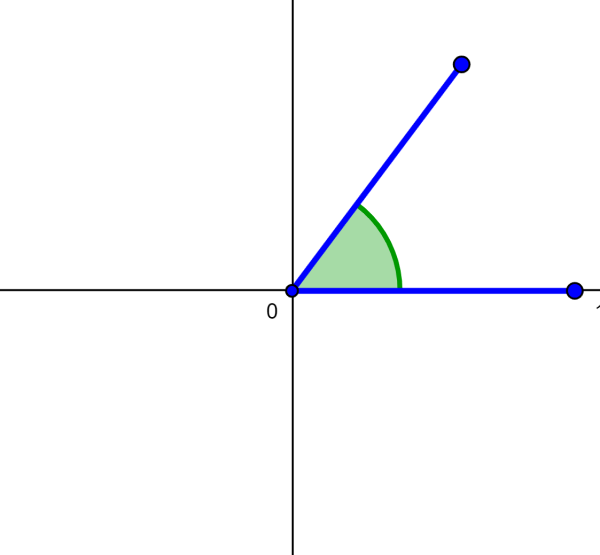
Acute angles
Acute angles are angles that have more than 0°, but less than 90°. Common examples of acute angles include 15°, 30°, 45°, 60°.
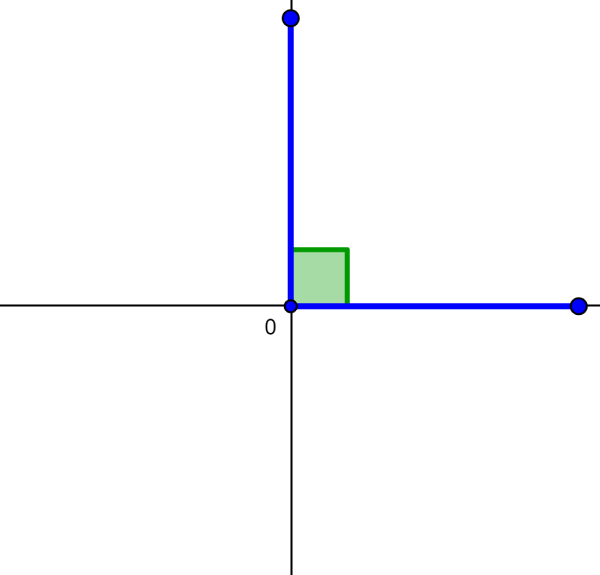
Right angles
A right angle is an angle that is exactly 90°. The two sides of a right angle are perpendicular to each other. These angles are represented by drawing a small square between the sides of the angle.
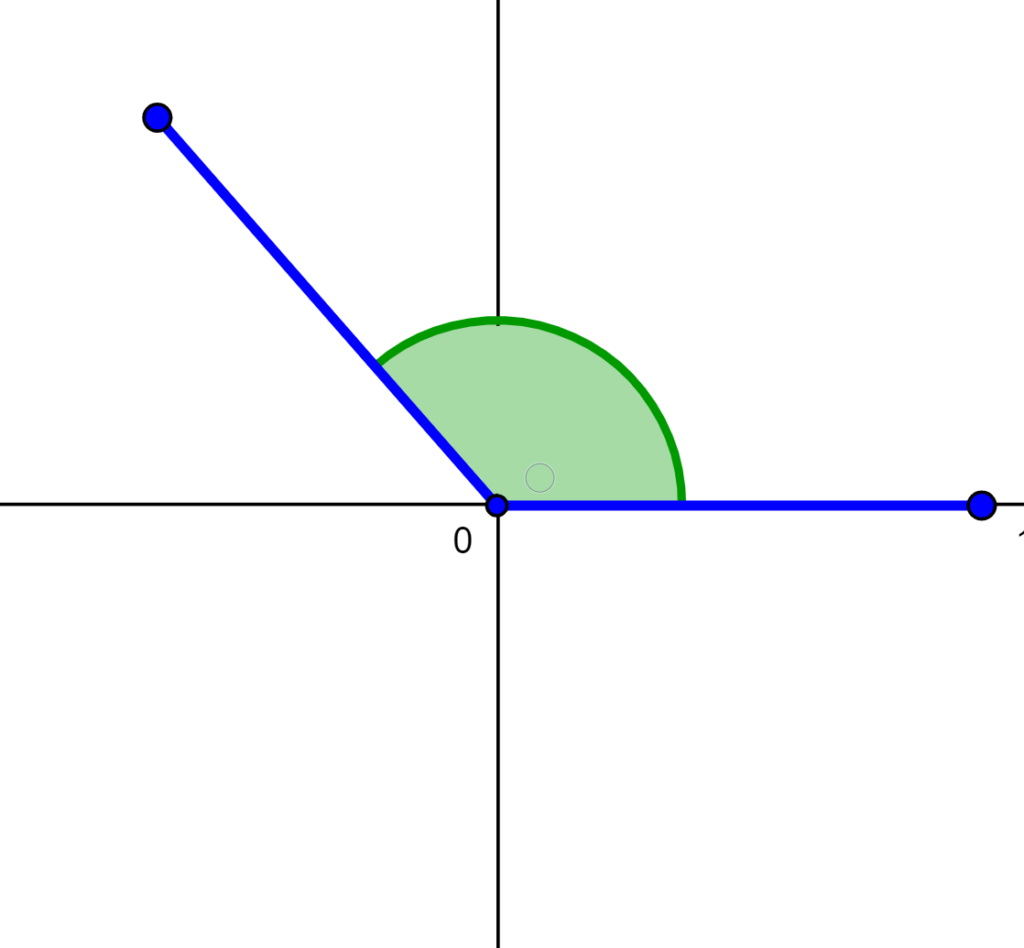
Obtuse angles
An obtuse angle is a type of angle that measures more than 90°, but less than 180°. Common examples of obtuse angles include 100°, 120°, 140°, 160°.
Straight angle
A straight angle has an exact measure of 180°. These angles are formed by straight lines.
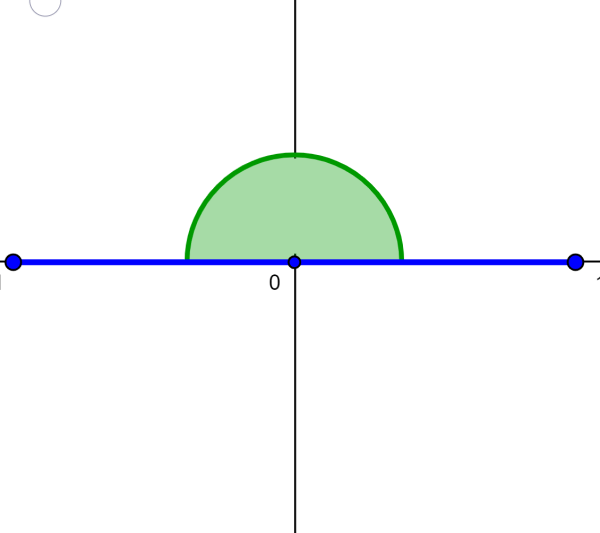
Oblique angle
Oblique angles are types of angles that are neither right nor multiples of a right angle. The acute and obtuse angles are oblique. Oftentimes, the term “oblique” is used to describe angles that measure more than 180°, but less than 360°.
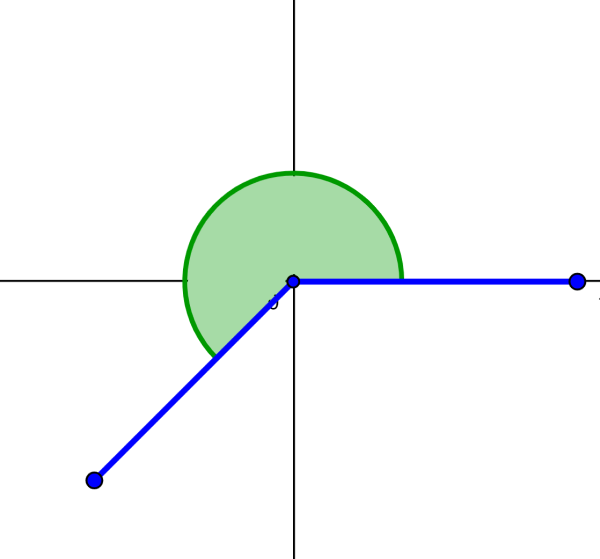
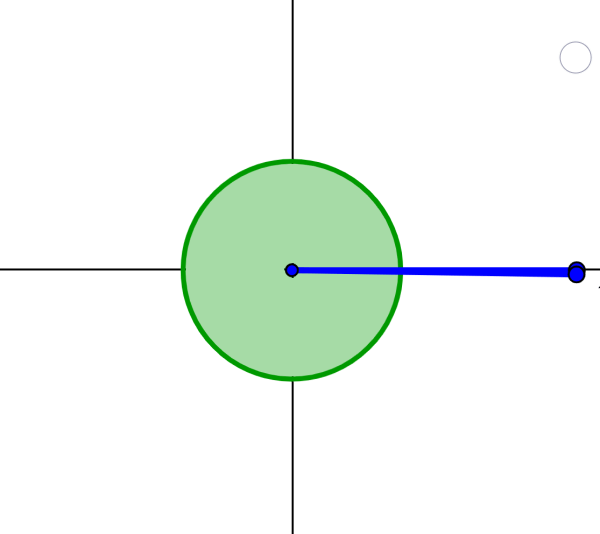
Full angle
A full angle is equal to 360°. These angles represent one complete revolution since 1 revolution is equivalent to 360°.
Types of angles based on their rotation
Based on the direction of rotation, the angles can be classified into two categories:
- Positive angles
- Negative angles
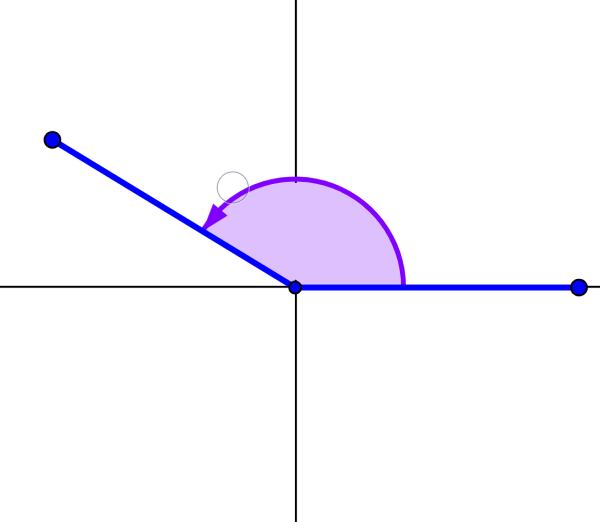
Positive angles
Positive angles are angles at which measurements are taken in a counterclockwise direction with respect to the base.
Negative angles
Negative angles are measured clockwise from the base.
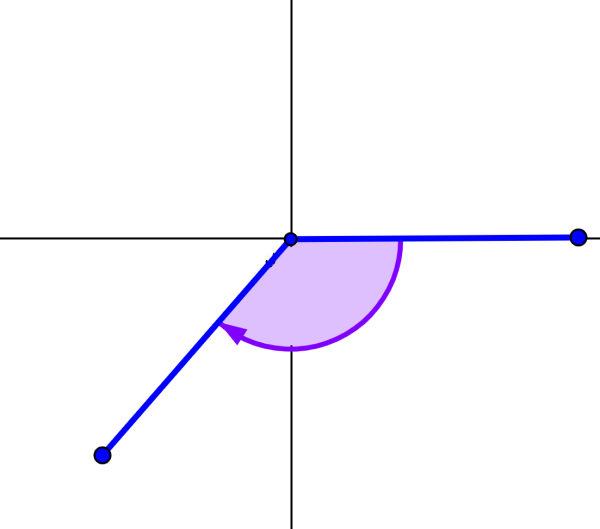
Other types of angles
There are other types of angles known as angle pairs. These angles appear as pairs and demonstrate some kind of property. These are:
- Adjacent angles
- Complementary angles
- Supplementary angles
- Opposite vertical angles
- Alternate internal angles
- Alternate exterior angles
- Corresponding angles
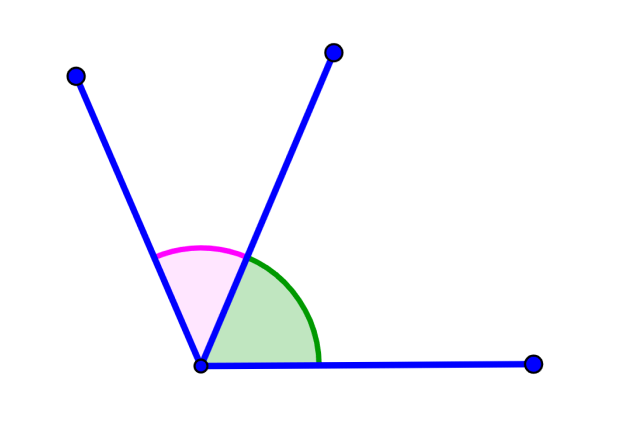
Adjacent angles
Adjacent angles share the same vertex and the same side. The other sides of these angles do not have a common point.
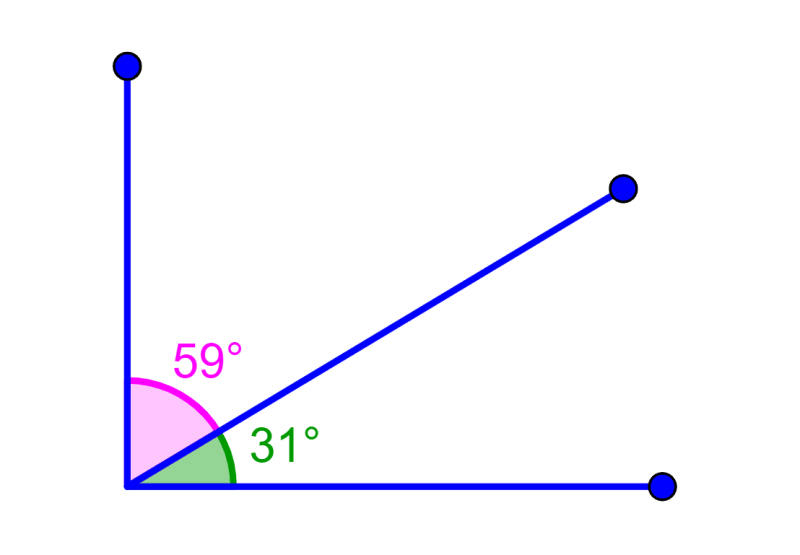
Complementary angles
Complementary angles are pairs of angles that add up to 90°.
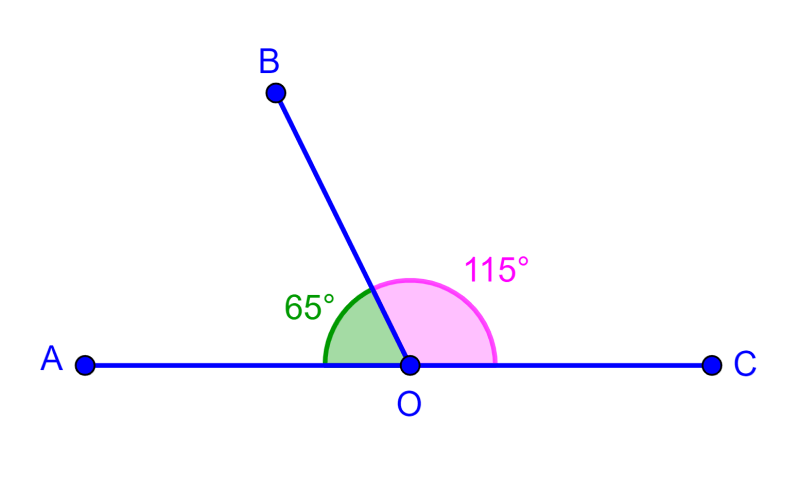
Supplementary angles
Supplementary angles are pairs of angles that add up to 180°.
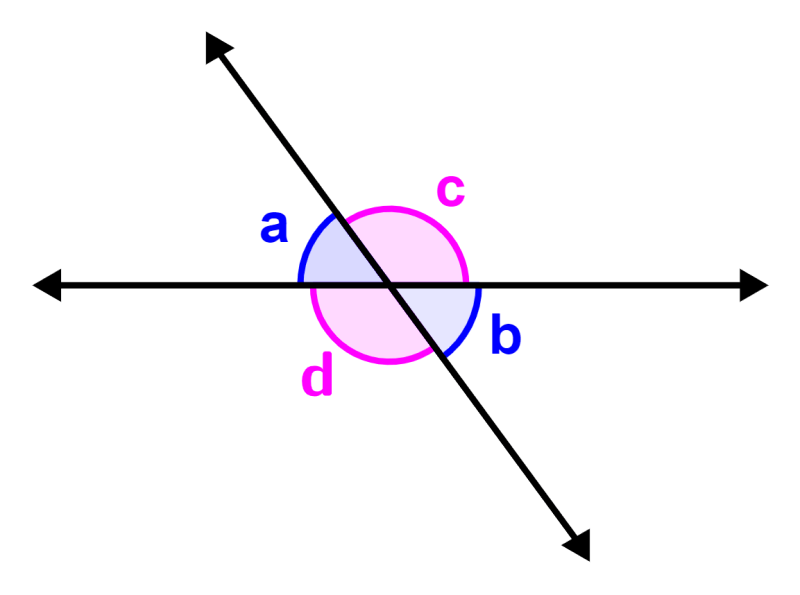
Opposite vertical angles
Opposite vertical angles are formed when two lines intersect. These angles have the same measure.
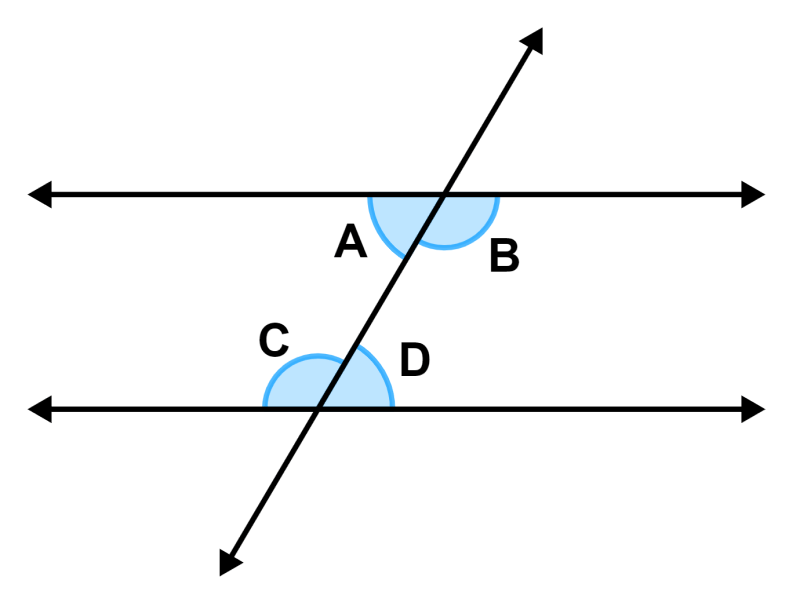
Alternate internal angles
Alternate interior angles are formed when a transverse line crosses two lines. If the lines are parallel, these angles are equivalent.
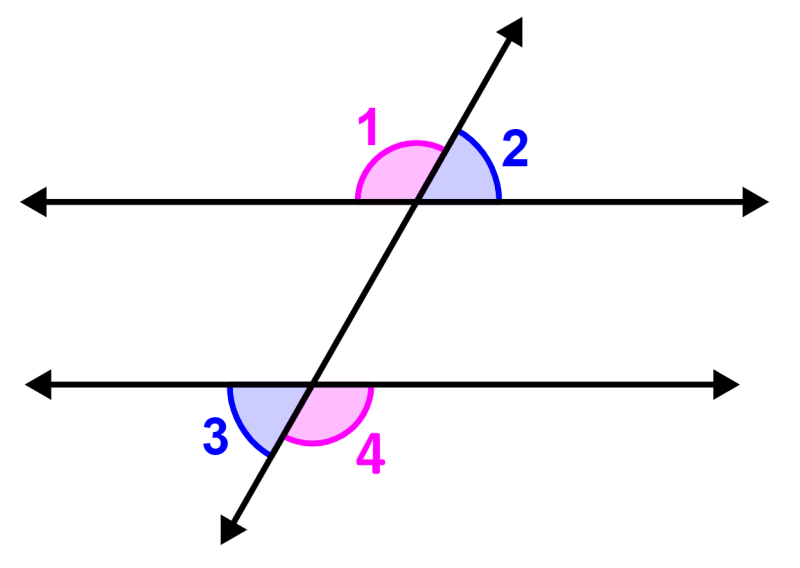
Alternate exterior angles
Similar to the previous ones, these angles are formed when a transversal line crosses two lines. When the two lines are parallel, these angles are the same.
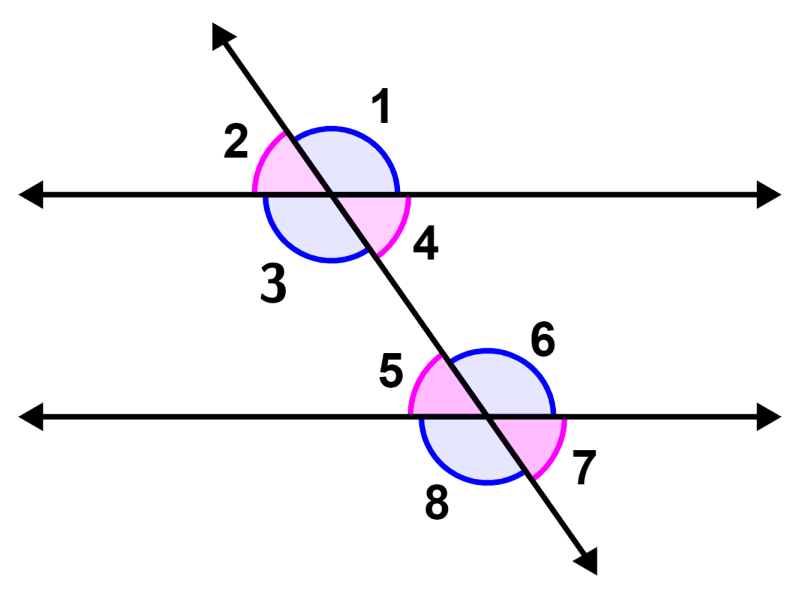
Corresponding angles
Corresponding angles are pairs of angles that are formed when a line intersects two parallel lines. The corresponding angles are equal to each other.
See also
Interested in learning more about angles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
