Dodecahedra are one of the five Platonic solids. We can calculate the volume of dodecahedra using a standard formula. On the other hand, the surface area is found by adding the areas of their twelve faces.
In this article, we will learn how to calculate the volume and surface area of a dodecahedron. We will learn how to derive the formulas and use it to solve several practice problems.
How to find the volume of a dodecahedron
A dodecahedron is a regular three-dimensional figure, so all of its faces have the same shape and all of its sides have the same length. Therefore, we can calculate its volume using the following formula:
| $$V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$ |
where a is the length of one of the sides of the dodecahedron.
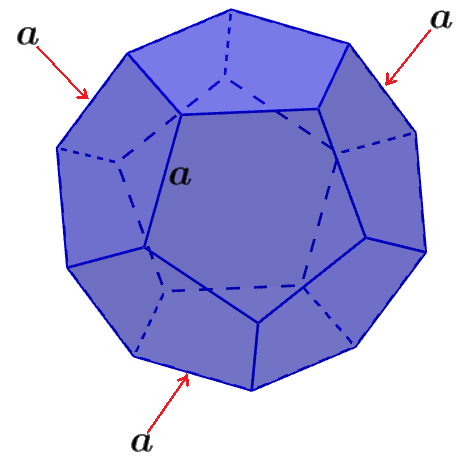
We can also simplify this formula by getting an approximation of the fraction on the right-hand side of the formula. Thus, we can write:
$latex V\approx 7.663{{a}^3}$
How to find the surface area of a dodecahedron
We can calculate the surface area of a dodecahedron using the following formula:
| $latex A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$ |
where a is the length of one of the sides of the dodecahedron.
We can simplify this formula by approximating the expression on the right-hand side of the formula. Therefore, we can write:
$latex A_{s}\approx 20.65{{a}^2}$
Derivation of the formula for the surface area of a dodecahedron
To find a formula for the surface area of a dodecahedron, we can consider that dodecahedrons are regular figures that have 12 faces with the same shape and dimensions.
Since all 12 pentagonal faces of the dodecahedron have the same dimensions, we just have to find the area of one of the faces and multiply the result by 12 to get the surface area of the dodecahedron.
Now, we can find the Area of a Pentagon using the following formula:
$$A=\frac{1}{4}\sqrt{25+10\sqrt{5}}~{{a}^2}$$
Therefore, when we multiply this formula by 12, we have:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
Volume and area of a dodecahedron – Examples with answers
EXAMPLE 1
What is the volume of a dodecahedron that has sides with a length of 2 inches?
Solution
We can use the formula for the volume of the dodecahedron with the value a=2. Therefore, we have:
$$V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$$V=\frac{15+7\sqrt{5}}{4}{{2}^3}$$
$$V=\frac{15+7\sqrt{5}}{4}8$$
$latex V=7.663\times 8$
$latex V=61.3$
The volume of the given dodecahedron is $latex 61.3~{{in}^3}$.
EXAMPLE 2
What is the surface area of a dodecahedron that has sides with a length of 1 in?
Solution
To solve this problem, we can apply the formula for the surface area of a dodecahedron with the value a=1. Therefore, we have:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{1}^2}$
$latex A_{s}=20.65$
The surface area of the dodecahedron is $latex 20.65~{{in}^2}$.
EXAMPLE 3
If a dodecahedron has sides 3 inches long, what is its volume?
Solution
Applying the volume formula with the value a=3, we have:
$$ V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$$ V=\frac{15+7\sqrt{5}}{4}{{3}^3}$$
$$ V=\frac{15+7\sqrt{5}}{4}27$$
$latex V=7.663\times 27$
$latex V=206.9$
The volume of the dodecahedron is $latex 206.9~{{in}^3}$.
EXAMPLE 4
Find the surface area of a dodecahedron that has sides with a length of 2 in.
Solution
Using the surface area formula with the value a=2, we have:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{2}^2}$
$latex A_{s}=20.65\times 4$
$latex A_{s}=82.6$
The surface area of the dodecahedron is $latex 82.6~{{m}^2}$.
EXAMPLE 5
Find the volume of a dodecahedron that has sides with a length of 8 ft.
Solution
Using the value of a=8 in the volume formula, we have:
$$V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$$V=\frac{15+7\sqrt{5}}{4}{{8}^3}$$
$$V=\frac{15+7\sqrt{5}}{4}512$$
$latex V=7.663\times 512$
$latex V=3923.5$
The volume of the given dodecahedron is $latex 3923.5~{{ft}^3}$.
EXAMPLE 6
Find the surface area of a dodecahedron that has sides with a length of 6 ft.
Solution
Applying the surface area formula using a=6, we have:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{6}^2}$
$latex A_{s}=20.65\times 36$
$latex A_{s}=743.4$
The surface area of the dodecahedron is $latex 743.4~{{ft}^2}$.
EXAMPLE 7
If the volume of a dodecahedron is equal to $latex 698.3~{{in}^3}$, what is the length of one of its sides?
Solution
In this case, we have the volume and we want to calculate the length of one of its sides. Thus, we use the volume formula and solve for a:
$$V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$$698.3=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$latex 698.3=7.663{{a}^3}$
$latex 91.13={{a}^3}$
$latex a=4.5$
The length of one of the sides of the dodecahedron is 4.5 in.
EXAMPLE 8
If a dodecahedron has a surface area of $latex 120~{{in}^2}$, what is the length of its sides?
Solution
In this problem, we know the surface area, and we need to determine the length of one of the sides of the dodecahedron. Therefore, we use the surface area formula and solve for a:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex 120=20.65~{{a}^2}$
$latex 5.81=a^2$
$latex a=2.41$
The dodecahedron has sides with a length of 2.41 in.
EXAMPLE 9
Find the length of the sides of a dodecahedron that has a volume of $latex 1077.5~{{ft}^3}$.
Solution
We use the volume formula and solve for a:
$$V=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$$1077.5=\frac{15+7\sqrt{5}}{4}{{a}^3}$$
$latex 1077.5=7.663{{a}^3}$
$latex 140.61={{a}^3}$
$latex a=5.2$
The length of one of the sides of the dodecahedron is 5.2 ft.
EXAMPLE 10
What is the length of the sides of a dodecahedron that has a surface area of $latex 350~{{ft}^2}$?
Solution
Similar to the previous problem, we are going to use the surface area formula and solve for a. Therefore, we have:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex 350=20.65~{{a}^2}$
$latex 16.95=a^2$
$latex a=4.12$
The dodecahedron has sides with a length of 4.12 ft.
Volume and area of a dodecahedron – Practice problems
If the surface area of a dodecahedron is equal to 495.7 m2, what is the length of its sides?
Write the answer to one decimal place.
See also
Interested in learning more about dodecahedrons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
