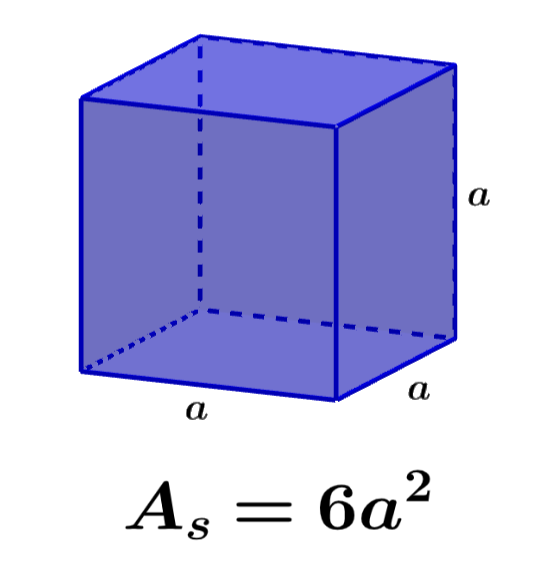
The surface area of a cube is equal to the sum of the areas of all the faces of the cube. We know that in a cube all the faces are equal, that is, they have the same area. Therefore, we can calculate its surface area by multiplying the area of one of its faces by six. Surface area is a useful measure when we want to measure a two-dimensional quantity in the cube. For example, if we want to paint a container that is cube-shaped, we can estimate the amount of paint we will need if we know its surface area.
Here, we will learn about the formula that we can use to calculate the surface area of a cube. In addition, we will look at some problems with which we will practice the use of this formula.
Formula to find the surface area of a cube
The surface area of a cube is equal to the sum of the areas of all the faces of the cube. Since the cube has six faces, we have to add the areas of the six faces to get its surface area.
We know that each face of the cube has a square shape. Therefore, the area of each face of the cube is equal to the square of the length of one of the sides. If we use a to represent the length of one of the sides, we have:
$latex \text{Area of a face}={{a}^2}$
If we add the six faces, we have:
$latex A_{S}={{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}$
| $latex A_{S}=6{{a}^2}$ |
where $latex A_{S}$ represents the surface area and a represents the length of one of the sides of the cube.
Surface area of a cube – Examples with answers
The following examples are solved using the formula for the surface area of cubes. It is recommended that you try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
What is the surface area of a cube that has sides of length 5 m?
Solution
We use the formula for surface area with the value $latex a=5$. Therefore, we have:
$latex A_{S}=6{{a}^2}$
$latex A_{S}=6{{(5)}^2}$
$latex A_{S}=6(25)$
$latex A_{S}=150$
The surface area is 150 m².
EXAMPLE 2
A cube has sides of length 10 m. What is its surface area?
Solution
We have the value $latex a=10$, so we use the formula for the surface area with that value:
$latex A_{S}=6{{a}^2}$
$latex A_{S}=6{{(10)}^2}$
$latex A_{S}=6(100)$
$latex A_{S}=600$
The surface area is 600 m².
EXAMPLE 3
If a cube has sides of length 12 m, what is its surface area?
Solution
Here, we have the value $latex a=12$, so by replacing in the formula, we have:
$latex A_{S}=6{{a}^2}$
$latex A_{S}=6{{(12)}^2}$
$latex A_{S}=6(144)$
$latex A_{S}=864$
The surface area is 864 m².
EXAMPLE 4
What is the length of the sides of a cube that has a surface area of 120 m²?
Solution
In this case, we start with the surface area and want to find the length of its sides, so we use the formula and solve for a:
$latex A_{S}=6{{a}^2}$
$latex 120=6{{a}^2}$
$latex 20={{a}^2}$
$latex a=4.47$
The length of the sides is 4.47 m.
EXAMPLE 5
If a cube has a surface area of 240 m², what is the length of its sides?
Solution
We are going to use the formula for the surface area with $latex A_{S}=240$ and solve for a:
$latex A_{S}=6{{a}^2}$
$latex 240=6{{a}^2}$
$latex 40={{a}^2}$
$latex a=6.32$
The length of the sides is 6.32 m.
Surface area of a cube – Practice problems
Use the following problems to practice using the formula for the surface area of cubes. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about cubes? Take a look at these pages: