The cube is one of the most common three-dimensional solid objects. The main characteristic of the cubes is that they have all their sides of the same length. The cubes have 6 faces, 12 edges, and 8 vertices. These figures have very common examples in real life, such as the Rubik’s cube and a standard 6-sided die.
Here, we will look at a more detailed definition of cubes and use diagrams to illustrate the concepts. Also, we will learn about the most important characteristics of the cubes. Finally, we will look at the most important formulas of these geometric figures and we will use them to solve some exercises.
Definition of a cube
The cube is a solid three-dimensional object bounded by six square faces. Three of these faces meet at each vertex. The cube is also defined as a hexahedron, that is, a solid with six faces. Cubes are a type of square prisms.
Many times, the shape of a cube is considered as a block, where the length, height, and width are all the same. Also, a main characteristic of cubes is that they have 6 faces, 8 vertices, and 12 edges. We can distinguish these elements in the following diagram.
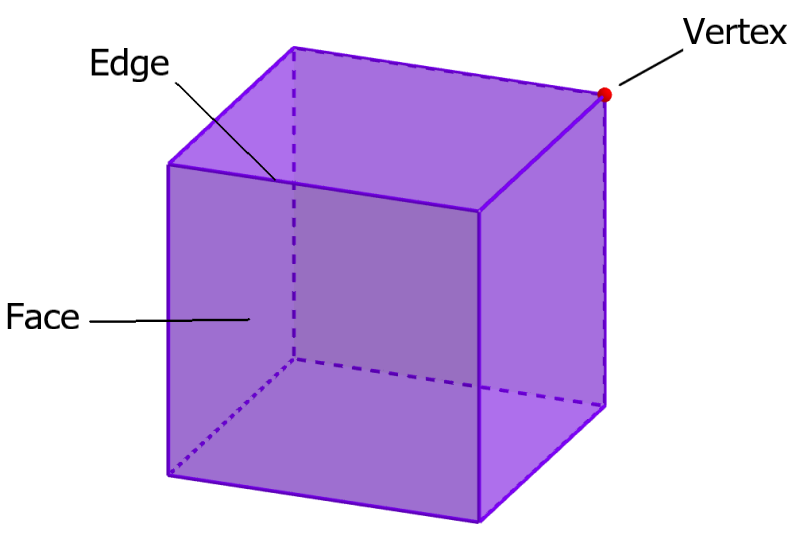
In the image, we can see the vertex, the face, and the edge. The faces of the cube are connected by four vertices. The edges of the cube are connected at a single point, which is the vertex. Since the cube is a 3D figure, the two important parameters used to measure the cube are volume and surface area.
Fundamental characteristics of a cube
The following are the most important characteristics of cubes:
- All their faces have a square shape.
- All faces and sides have equal dimensions.
- Each of the faces meets four faces.
- The interior angles of the cube are right angles.
- Each of the vertices meets three faces and three edges.
- The edges opposite each other are parallel.
Important cube formulas
The most important cube formulas for solving exercises are the volume formula, the surface area formula, and the diagonal formula.
Formula for the volume of a cube
The volume of a cube can be calculated by multiplying the lengths of its three dimensions. Since all the sides have the same measure, we have:
| $latex V={{a}^3}$ |
where a is the length of the sides of the cube.
Formula for the surface area of a cube
The surface area is the sum of the areas of all the faces of the cube. We know that we have six equal faces in a cube and also that the area of a face is equal to the area of a square, so we have:
| $latex A_{s}=6{{a}^2}$ |
where a is the length of one of the sides.
Formula for the diagonal of a cube
The formula for the diagonal of a cube is derived by using the Pythagorean theorem twice. Then, simplifying, we have the following expression:
| $latex d=\sqrt{3}~a$ |
where d represents the length of the diagonal and a represents the length of one of the sides.
Examples of cube problems
The following examples are solved by applying the cube formulas seen above.
EXAMPLE 1
What is the volume of a cube that has sides of length 8 m?
Solution: We use the length $latex a = 8$ in the volume formula. Therefore, we have:
$latex V={{a}^3}$
$latex V={{8}^3}$
$latex V=512$
The volume of the cube is 512 m³.
EXAMPLE 2
A cube has sides of length 10 m. What is its surface area?
Solution: We have the length $latex a=10$, so we use this value in the formula for surface area:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(10)}^2}$
$latex A_{s}=6(100)$
$latex A_{s}=600$
The surface area is 600 m².
EXAMPLE 3
If a cube has sides of length 20 m, what is the length of its diagonal?
Solution: We use the length $latex a=20$ in the formula for the diagonal. Therefore, we have:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(20)$
$latex d=34.64$
The length of the diagonal is 34.64 m.
See also
Interested in learning more about cubes? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
