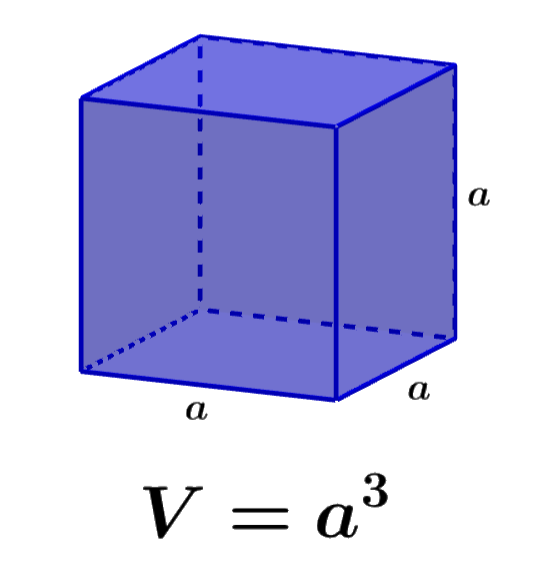
The volume of a cube defines the number of cubic units that are completely occupied by the cube. A cube is a solid and a three-dimensional figure, which has six square faces. To calculate the volume, we need to know the dimension of its sides. Since a cube has all its sides of the same length, we can find the volume of the cube by raising one of its sides to the power of 3.
Here, we will learn about the formula we can use to find the volume of cubes. We will learn to derive this formula and use it to solve some exercises.
Formula to find the volume of a cube
We can easily calculate the volume of cubes if we know the length of one of their sides. Volume is the product of length, width, and height. In the case of cubes, we know that all their sides have equal lengths, so we have:
Volume = Length × Width × Height
$latex V=a\times a \times a$
| $latex V={{a}^3}$ |
where a is the length of one of the sides of the cube.
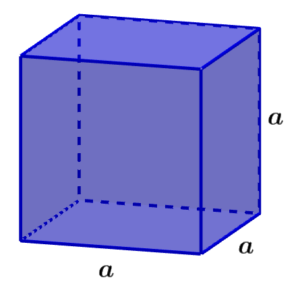
Derivation of the volume formula
We know that a cube is a three-dimensional object that has length, width, and height with the same length. We can derive its formula for volume as follows:
- Let’s consider a square sheet of paper.
- The area of that square sheet will be equal to its length multiplied by its width.
- Since the length and width are equal in a square, its area will be $latex {{a}^2}$.
- A cube is formed by stacking several sheets of paper one on top of the other until obtaining a height equal to a.
- We can conclude that the volume covered by the cube is equal to the area of the base multiplied by the height.
- Therefore, the volume of the cube is equal to $latex {{a}^3}$.
Formula to find the volume of a cube using the diagonal
It is also possible to calculate the volume of a cube using the length of the diagonal. For this, we can use the following formula:
| $latex V=\sqrt{3} \times \frac{{{d}^3}}{9}$ |
where d is the length of the diagonal of a cube.
Volume of a cube – Examples with answers
The following examples can be used to practice applying the formulas for the volume of cubes. Each example has its respective solution, where the process and reasoning used are detailed.
EXAMPLE 1
What is the volume of a cube that has sides of length 5 m?
Solution
We can use the first formula for the volume with the length $latex a=5$. Therefore, we have:
$latex V=a^3$
$latex V={{5}^3}$
$latex V=125$
The volume is equal to 125 m³.
EXAMPLE 2
If a cube has sides of length 10 m, what is its volume?
Solution
We have the length $latex a=10$, so we plug this value into the volume formula:
$latex V=a^3$
$latex V={{10}^3}$
$latex V=1000$
The volume is equal to 1000 m³.
EXAMPLE 3
A cube has a volume of 512 cm³. What is the length of one of its sides?
Solution
In this case, we start with the area and want to find the length of one of the sides. We use the volume formula and solve for a:
$latex V=a^3$
$latex 512={{a}^3}$
$latex a=8$
The length of one of the sides is 8 cm³.
EXAMPLE 4
What is the volume of a cube that has a diagonal of 5 m?
Solution
Here, we have the length $latex d=5$, so we use the second formula with this value:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{5}^3}}{9}$
$latex V=\sqrt{3}\times \frac{125}{9}$
$latex V=24.1$
The volume is equal to 24.1 m³.
EXAMPLE 5
A cube has a diagonal of 10 m. What is its volume?
Solution
We have the length $latex d=10$, so we use the second formula with this value:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{10}^3}}{9}$
$latex V=\sqrt{3}\times \frac{1000}{9}$
$latex V=192.5$
The volume is equal to 192.5 m³.
Volume of a cube – Practice problems
Put into practice the formulas for the volume of cubes seen above to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about cubes? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
