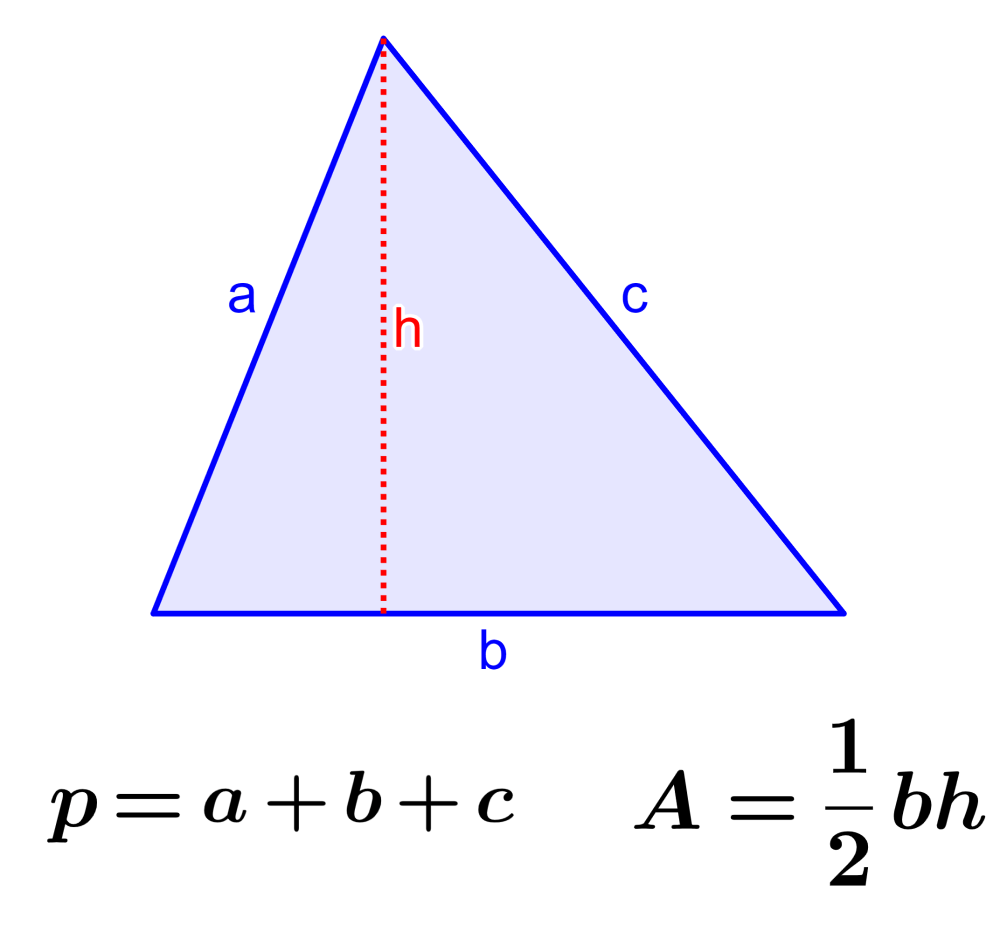The perimeter of a triangle is the length of the contour around the triangle. On the other hand, the area of the triangle is a two-dimensional measurement that represents the space occupied by the figure. The perimeter of a triangle can be found by adding the lengths of its three sides, and its area can be found by multiplying the product of its base and height by one-half.
In this article, we will learn all about the perimeter and area of triangles. We will explore the formulas of scalene, isosceles and equilateral triangles.
How to find the perimeter of a triangle?
To find the perimeter of any triangle, we have to add the lengths of its three sides. In the case of a scalene triangle, we have the following formula:
| $latex p=a+b+c$ |
where, $latex a,~b,~c$ are the lengths of the sides of the triangle.
Calculate the perimeter of an isosceles triangle
An isosceles triangle has two sides that have the same length and a third side that has a different length. Therefore, we can calculate its perimeter with the following formula:
| $latex p=b+2a$ |
where, b is the length of the base and a is the length of the congruent sides.
Calculate the perimeter of an equilateral triangle
An equilateral triangle has all three sides of the same length. Therefore, to calculate the perimeter of an equilateral triangle, we have to multiply the length of one of the triangle’s sides by 3:
| $latex p=3a$ |
where, a is the length of one side of the triangle.
How to find the area of a triangle?
The area of any triangle can be found by multiplying the product of its base and height by one-half. Therefore, we have the following formula:
| $latex \text{Area}= \frac{1}{2} \times \text{base} \times \text{height}$ $latex A=\frac{1}{2} \times b \times h$ |
where, b is the length of the base and h is the length of the height.
Calculate the area of an isosceles triangle
We can obtain a formula for the area of an isosceles triangle by expressing its height in terms of its sides. Therefore, recalling that the Height of an Isosceles Triangle can be calculated using the following formula:
$latex h=\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}$
we can substitute it in the formula for the area of a triangle to have the following formula:
| $latex A=\frac{1}{2}(\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}\times b)$ |
where
- b is the length of the base of the isosceles triangle
- h is the height of the triangle
- a is the length of the congruent sides of the isosceles triangle
Calculate the area of an equilateral triangle
The area of an equilateral triangle can be calculated using a formula expressed in terms of the length of its sides. Therefore, recalling that the formula for the Height of an Equilateral Triangle is as follows:
$latex h=\frac{\sqrt{3}~a}{2}$
we can substitute it in the formula for the area of a triangle to obtain the following formula:
| $latex A= \frac{ \sqrt{3}}{4}{{a}^2}$ |
where, a is the length of one of the sides of the equilateral triangle.
Perimeter and area of a triangle – Examples with answers
The different formulas for the perimeter and area of a triangle are used to solve the following examples. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Determine the perimeter of a scalene triangle that has sides with the lengths 4 inches, 6 inches, and 8 inches.
Solution
To find the perimeter, we need to add the lengths of the three sides of the scalene triangle. Therefore, we have:
$latex p=a+b+c$
$latex p=4+6+8$
$latex p=18$
The perimeter of the triangle is equal to 18 inches.
EXAMPLE 2
Find the area of a scalene triangle that has a base with a length of 6 inches and a height of 7 inches.
Solution
We have the following lengths:
- Height, $latex h=7$ in
- Base, $latex b=6$ in
No matter what type of triangle it is, we can calculate its area as follows:
$latex A= \frac{1}{2} \times b \times h$
$latex A= \frac{1}{2} (6)(7)$
$latex A=21$
The area of the triangle is equal to 21 in².
EXAMPLE 3
Find the perimeter of an isosceles triangle that has a base of 12 feet and congruent sides of 15 feet.
Solution
We have the following information:
- Base, $latex b=12$ ft
- Sides, $latex a=15$ ft
We use the formula for the perimeter of an isosceles triangle:
$latex p=b+2a$
$latex p=12+2(15)$
$latex p=12+30$
$latex p=42$
The perimeter of the triangle is equal to 42 ft.
EXAMPLE 4
What is the area of an isosceles triangle that has a height of 11 yards and a base of 10 yards?
Solution
We have the following information:
- Height, $latex h=11$ yd
- Base, $latex b=10$ yd
We use the formula for the area of a triangle with the given lengths:
$latex A= \frac{1}{2} \times b \times h$
$latex A= \frac{1}{2} (10)(11)$
$latex A=55$
The area of the triangle is equal to 55 yd².
EXAMPLE 5
If an isosceles triangle has congruent sides of 22 feet and a base of 15 feet, what is its perimeter?
Solution
We have the following information:
- Base, $latex b=15$ ft
- Sides, $latex a=22$ ft
Therefore, we use the formula for the perimeter of an isosceles triangle, and we have:
$latex p=b+2a$
$latex p=15+2(22)$
$latex p=15+44$
$latex p=59$
The perimeter of the triangle is equal to 59 feet.
EXAMPLE 6
Find the area of an equilateral triangle that has sides with a length of 10 inches.
Solution
We use the formula for the area of an equilateral triangle with length a=10:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{10}^2})$
$latex A= \frac{ \sqrt{3}}{4}(100)$
$latex A=43.3$
The area of the equilateral triangle is equal to 43.3 in².
EXAMPLE 7
Find the perimeter of an equilateral triangle that has side lengths of 11 feet.
Solution
To find the perimeter of the triangle, we add the lengths of its three sides. However, since the triangle is equilateral, we can multiply the length of one side by 3:
$latex p=3a$
$latex p=3(11)$
$latex p=33$
The perimeter is equal to 33 ft.
EXAMPLE 8
What is the area of an equilateral triangle that has sides with a length of 14 inches?
Solution
Using the formula for the area of an equilateral triangle with a=14, we have:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{14}^2})$
$latex A= \frac{ \sqrt{3}}{4}(196)$
$latex A=84.87$
The area of the equilateral triangle is equal to 84.87 in².
EXAMPLE 9
Find the perimeter of an equilateral triangle that has sides with a length of 15 yards.
Solution
Using the formula for the perimeter of an equilateral triangle with the length a=15, we have:
$latex p=3a$
$latex a=3(15)$
$latex a=45$
The perimeter of the triangle is equal to 45 yd.
EXAMPLE 10
Find the area of an isosceles triangle that has a base with a length of 12 inches and congruent sides with a length of 14 inches.
Solution
We have the following:
- Base, $latex b=12$ in
- Congruent sides, $latex a=14$ in
We can use the formula for the area of an isosceles triangle in terms of its sides:
$latex h=\frac{1}{2}(\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}\times b)$
$latex h=\frac{1}{2}(\sqrt{{{14}^2}-\frac{{{12}^2}}{4}}\times 12)$
$latex h=\frac{1}{2}(\sqrt{196-\frac{144}{4}}\times 12)$
$latex h=\frac{1}{2}(\sqrt{196-36}\times 12)$
$latex h=\frac{1}{2}(\sqrt{160}\times 12)$
$latex h=\frac{1}{2}(12.65 \times 12)$
$latex h=\frac{1}{2}(151.8)$
$latex h=75.9$
The area of the triangle is equal to 75.9 in².
Perimeter and area of a triangle – Practice problems
Use everything you have learned about the perimeter and area of a triangle to solve the following problems.
See also
Interested in learning more about the perimeter and area of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
