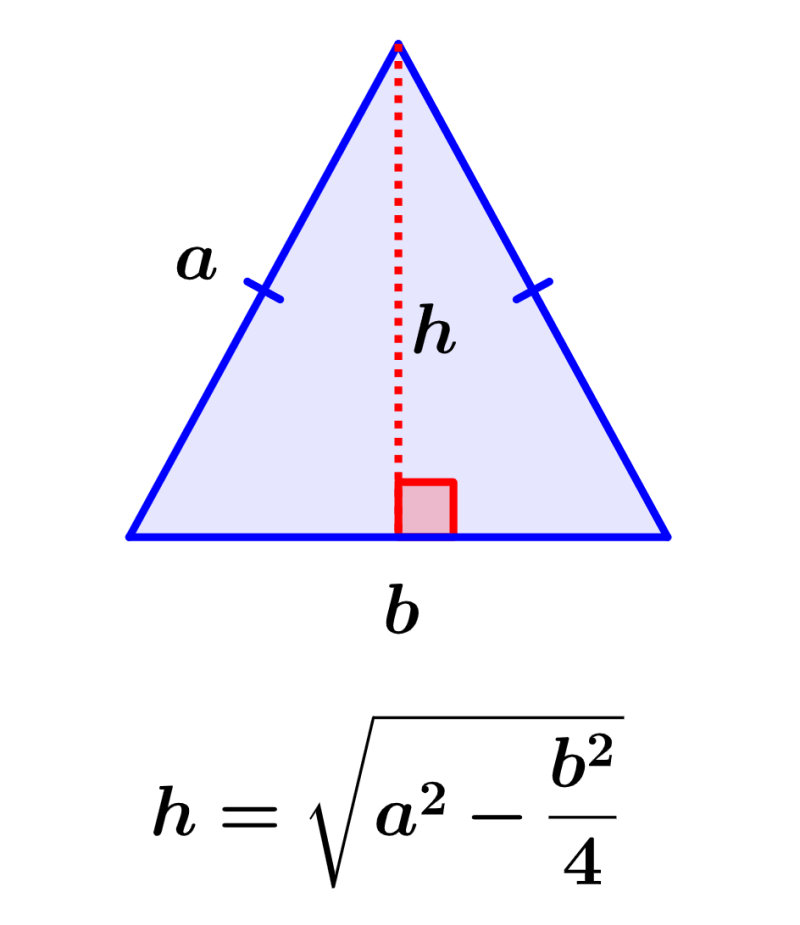
The height of an isosceles triangle is the perpendicular distance from the base of the triangle to the opposite vertex. The height of a triangle is one of its important dimensions because it allows us to calculate the area of the triangle.
To find the length of the height of an isosceles triangle, we have to use the Pythagoras theorem to derive a formula.
GEOMETRY
Relevant for…
Learning about the height of an isosceles triangle with examples.
GEOMETRY
Relevant for…
Learning about the height of an isosceles triangle with examples.
Formula for the height of an isosceles triangle
The height of an isosceles triangle is calculated using the length of its base and the length of one of the congruent sides. We can calculate the height using the following formula:
| $latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$ |
where a is the length of the congruent sides of the triangle and b is the length of the base of the triangle.
Derivation of the height formula
To derive this formula, we can consider the following isosceles triangle:
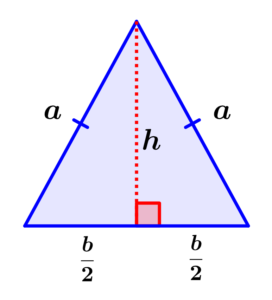
By drawing a line representing the height, we can see that we divide the isosceles triangle into two congruent right triangles. We can use one of the obtained triangles and apply the Pythagorean theorem to calculate the height.
Recall that the Pythagorean theorem does not say that the square of the hypotenuse is equal to the sum of the squares of the legs. Therefore, we have:
$latex {{a}^2}={{h}^2}+{{( \frac{b}{2})}^2}$
$latex {{a}^2}={{h}^2}+ \frac{{{b}^2}}{4}$
$latex {{h}^2}={{a}^2}- \frac{{{b}^2}}{4}$
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
We have obtained an expression for the height.
Height of an isosceles triangle – Examples with answers
The following examples use the seen formula to find the height of isosceles triangles. Try to solve the exercises yourself before looking at the solution.
EXAMPLE 1
What is the height of an isosceles triangle that has a base of 8 m and congruent sides of length 6 m?
Solution
From the question, we have the following data:
- Base, $latex b=8$ m
- Sides, $latex a=6$ m
Therefore, we use the height formula with these values:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{6}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{36- \frac{64}{4}}$
$latex h= \sqrt{36-16}$
$latex h= \sqrt{20}$
$latex h=4.47$
The height of the triangle is 4.47 m.
EXAMPLE 2
An isosceles triangle has a base of 10 m and congruent sides of length 12 m. What is the length of its height?
Solution
We can identify the following information:
- Base, $latex b=10$ m
- Sides, $latex a=12$ m
Substituting these values in the formula, we have:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{12}^2}- \frac{{{10}^2}}{4}}$
$latex h= \sqrt{144- \frac{100}{4}}$
$latex h= \sqrt{144-25}$
$latex h= \sqrt{119}$
$latex h=10.91$
The height of the triangle is 10.91 m.
EXAMPLE 3
An isosceles triangle has a base of length 8 m and congruent sides of length 9 m. What is the length of the height?
Solution
From the question, we have the following values:
- Base, $latex b=8$ m
- Sides, $latex a=9$ m
Substituting these values in the height formula, we have:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{9}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{81- \frac{64}{4}}$
$latex h= \sqrt{81-16}$
$latex h= \sqrt{65}$
$latex h=8.06$
The height of the triangle is 8.06 m.
EXAMPLE 4
What is the height of a triangle that has a base of length 14 m and congruent sides of length 11 m?
Solution
We have the following information:
- Base, $latex b=14$ m
- Sides, $latex a=11$ m
Therefore, we use the height formula with these values:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{11}^2}- \frac{{{14}^2}}{4}}$
$latex h= \sqrt{121- \frac{196}{4}}$
$latex h= \sqrt{121-49}$
$latex h= \sqrt{72}$
$latex h=8.49$
The height of the triangle is 8.49 m.
Height of an isosceles triangle – Practice problems
Use the formula for the height of isosceles triangles to solve the following problems. If you need help, you can look at the solved examples above.
See also
Interested in learning more about isosceles triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
