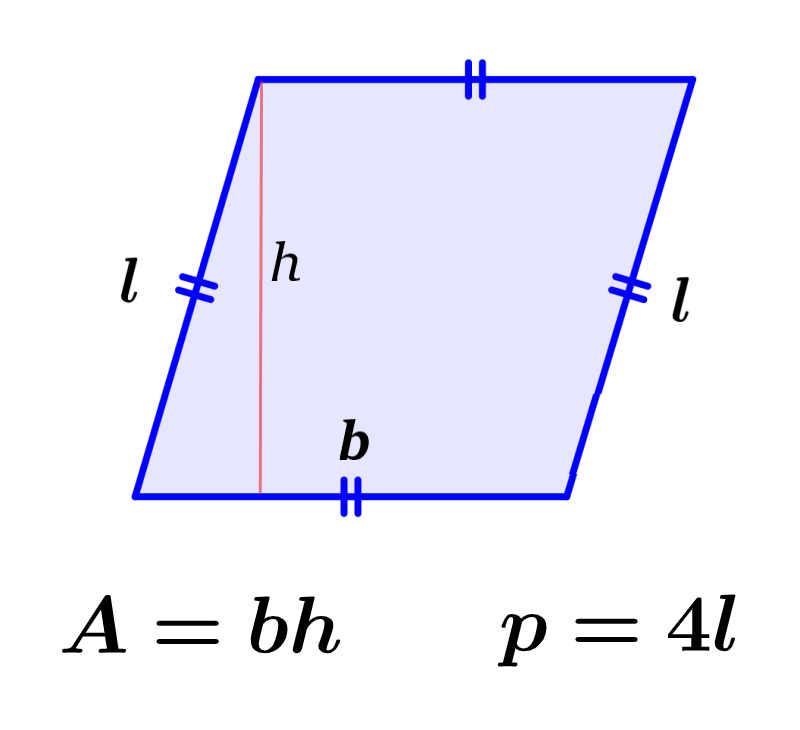
The perimeter of a rhombus represents the length of its outline. On the other hand, the area of the rhombus is a measure of the space occupied by the rhombus in two-dimensional space. The perimeter of a rhombus can be calculated using the formula p = 4l, where l is the length of a side, and its area can be calculated using the formula A = bh, where b is the base and h is its height.
In this article, we will learn about the perimeter and area of a rhombus. We will explore the different formulas that we can use, and we will apply them to solve some practice problems.
How to find the perimeter of a rhombus?
To calculate the perimeter of a rhombus, we have to add the lengths of all its sides. Since a rhombus is a quadrilateral with four equal sides, the formula for the perimeter of a rhombus can be written as:
| $latex p=4l$ |
where,
- p is the perimeter of the rhombus
- l is the length of one of the sides of the rhombus
This means that to calculate the perimeter of a rhombus, we only need to know the length of one of its sides.
How to find the area of a rhombus?
The area of a rhombus can be calculated using three different methods depending on the information available to us. We can use its diagonals, we can use its base and height, and we can use trigonometry.
Calculate the area of the rhombus using diagonals
We can calculate the area of a rhombus when we know the length of its diagonals by using the following formula:
| $latex A=\frac{d_{1}\times d_{2}}{2}$ |
where,
- $latex d_{1}=$ length of diagonal 1
- $latex d_{2}=$ length diagonal 2
- $latex A=$ area of rhombus
Proof of the formula for the area of a rhombus
We can prove the formula for the area of a rhombus using the following diagram:
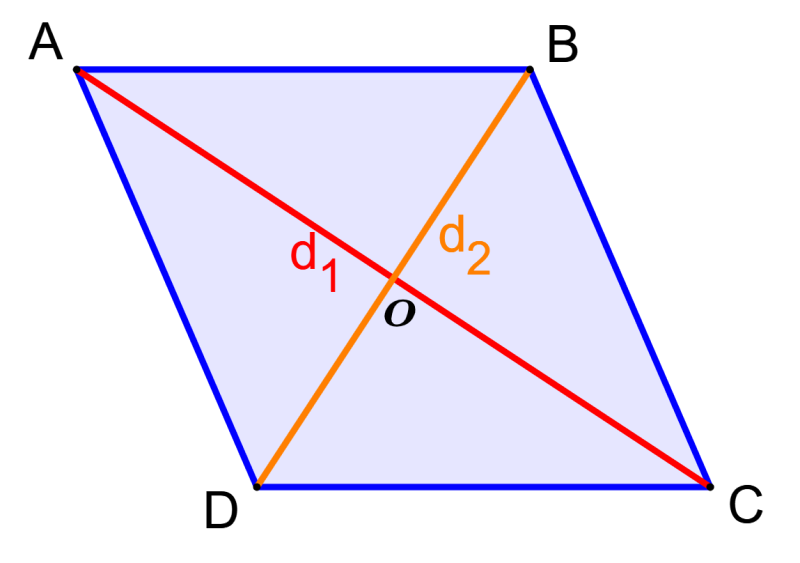
Point O is the point of intersection of the two diagonals of the rhombus. Therefore, the area of the rhombus will be:
$latex A=4\times\text{área de }\Delta AOB$
$latex =4\times(\frac{1}{2})\times AO \times OB$
$latex =4\times(\frac{1}{2})\times(\frac{1}{2})d_{1}\times(\frac{1}{2})d_{2}$
$latex =4\times(\frac{1}{8})d_{1}d_{2}$
$latex =\frac{1}{2}d_{1}d_{2}$
Calculate the area of the rhombus using the base and height
When we know the length of the base and the length of the height of the rhombus, we can use the following formula to calculate its area:
| $latex A=bh$ |
where,
- $latex b=$ length of any side of the rhombus
- $latex h=$ height
- $latex A=$ area of rhombus
Calculate the area of the rhombus using trigonometry
We can use trigonometry to calculate the area of the rhombus when we know the measure of one angle of the rhombus. Therefore, we use the following formula:
| $latex A={{b}^2}\times \sin(a)$ |
where,
- $latex b=$ length of any side of the rhombus
- $latex a=$ internal angle
- $latex A=$ area of rhombus
Perimeter and area of a rhombus – Examples with answers
EXAMPLE 1
What is the perimeter of a rhombus that has sides with a length of 7 inches?
Solution
The sides of the rhombus have a length of 7 inches. Therefore, we use that length in the formula for the perimeter:
$latex p=4l$
$latex p=4(7)$
$latex p=28$
The perimeter of the rhombus is equal to 28 inches.
EXAMPLE 2
What is the area of a rhombus that has diagonals with lengths of 8 inches and 10 inches?
Solution
We have the following lengths:
- Diagonal 1, $latex d_{1}=8$ in
- Diagonal 2, $latex d_{2}=10$ in
Using the area formula with these values, we have:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{8\times 10}{2}$
$latex =\frac{80}{2}$
$latex A=40$
Therefore, the area of the rhombus is equal to 40 in².
EXAMPLE 3
Find the perimeter of a rhombus that has sides with a length of 12 ft.
Solution
Using the formula for the perimeter with the given length, we have:
$latex p=4l$
$latex p=4(12)$
$latex p=48$
The perimeter of the rhombus is equal to 48 ft.
EXAMPLE 4
Find the area of a rhombus that has diagonals with lengths of 10 feet and 12 feet.
Solution
We have the following lengths:
- Diagonal 1, $latex d_{1}=10$ ft
- Diagonal 2, $latex d_{2}=12$ ft
Using these lengths in the formula for the area, we have:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{10\times 12}{2}$
$latex =\frac{120}{2}$
$latex A=60$
Therefore, the area of the rhombus is equal to 60 ft².
EXAMPLE 5
Find the perimeter of a rhombus that has sides with a length of 15 yards.
Solution
We apply the formula for the perimeter with the given length:
$latex p=4l$
$latex p=4(15)$
$latex p=60$
The perimeter of the rhombus is equal to 60 yd.
EXAMPLE 6
Find the area of a rhombus that has a base of 8 feet and a height of 6 feet.
Solution
We have the following lengths:
- Base, $latex b=8$ ft
- Height, $latex h=6$ ft
Applying the formula for the area with the given information, we have:
$latex A=bh$
$latex =(8)(6)$
$latex A=48$
Therefore, the area of the rhombus is equal to 48 ft².
EXAMPLE 7
What is the length of the sides of a rhombus that has a perimeter equal to 36 yards?
Solution
In this example, we know the perimeter, and we want to find the length of one of the sides of the rhombus. Therefore, we use the formula for the perimeter and solve for l:
$latex p=4l$
$latex 36=4l$
$latex l=9$
The length of one side of the rhombus is 9 yd.
EXAMPLE 8
Find the area of a rhombus that has sides with a length of 10 feet and an internal angle of 60°.
Solution
We have the following information:
- Side, $latex b=10$ ft
- Angle, $latex a=60°$
Using the formula for the area of a rhombus with this information, we have:
$latex A={{b}^2}\times \sin(60°)$
$latex ={{10}^2}\times 0.866$
$latex =100\times 0.866$
$latex A=866$
Therefore, the area of the rhombus is equal to 866 ft².
EXAMPLE 9
Find the length of the sides of a rhombus that has a perimeter equal to 68 inches.
Solution
We use the formula for the perimeter of a rhombus and solve for l:
$latex p=4l$
$latex 68=4l$
$latex l=17$
The length of one of the sides of the rhombus is equal to 17 in.
EXAMPLE 10
Find the area of a rhombus that has a base 5.5 inches long and a height 6.5 inches long.
Solution
We have the following:
- Base, $latex b=5.5$ in
- Height, $latex h=6.5$ in
When we apply the formula for the area, we have:
$latex A=bh$
$latex =(5.5)(6.5)$
$latex A=35.75$
Therefore, the area of the rhombus is equal to 35.75 in².
Perimeter and area of a rhombus – Practice problems
See also
Interested in learning more about the perimeter and area of geometric figures? Take a look at these pages: