An obtuse scalene triangle is a scalene triangle that has an obtuse internal angle. These triangles are scalenes and obtuse at the same time. Recall that an obtuse angle is an angle that is greater than 90 degrees and a scalene triangle is a triangle that has all its sides with different lengths and all of its angles with different measures.
Here, we will learn more about obtuse scalene triangles. We will also learn some of its characteristics and its most important formulas. In addition, we will use those formulas to solve some exercises.
What are obtuse scalene triangles?
An obtuse scalene triangle is a triangle that is scalene and obtuse at the same time. Scalene triangles are characterized by having sides of different lengths, that is, no side of a scalene triangle is similar to another. Furthermore, scalene triangles also have angles that are different from each other.
An obtuse triangle is characterized by having an internal angle greater than 90 degrees. The following is an example of an obtuse scalene triangle:
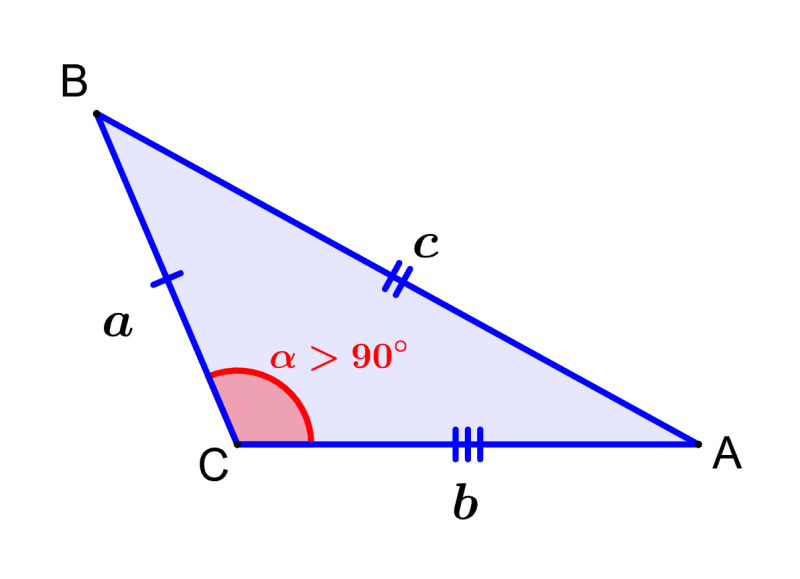
Formulas for obtuse scalene triangles
The obtuse scalene triangles have the same important formulas as the “normal” scalene triangles.
Area of scalene triangles
We can calculate the area of scalene triangles by multiplying the product of the base and the height by one half:
| $latex A=\frac{1}{2}\times b \times h$ |
where b represents the length of the base and h represents the length of the height.
Perimeter of scalene triangles
The perimeter of scalene triangles is equal to the sum of the lengths of all their sides:
| $latex p=a+b+c$ |
where, $latex a, ~ b, ~ c$ represent the lengths of the sides of the obtuse scalene triangle.
Obtuse scalene triangles – Examples with answers
EXAMPLE 1
We have a scalene triangle with a base of 16 m and a height of 18 m. What is its area?
Solution: We can use the area formula with the given information:
$latex A=\frac{1}{2}\times b \times h$
$latex A=\frac{1}{2}\times 16 \times 18$
$latex A=144$
The area is 144 m².
EXAMPLE 2
What is the perimeter of a scalene triangle that has sides of lengths 21 m, 23 m, 26 m?
Solution: We plug the lengths of the sides into the perimeter formula:
$latex p=a+b+c$
$latex p=21+23+26$
$latex p=70$
The perimeter is 70 m.
EXAMPLE 3
What is the length of the height of a triangle if its area is 50 m² and its base is 10?
Solution: We use the area formula and solve for h which is the height:
$latex A=\frac{1}{2}\times b\times h$
$latex 50=\frac{1}{2}\times 10\times h$
$latex 50=5h$
$latex h=10$
The height is 10 m.
Scalene triangle – Practice problems
See also
Interested in learning more about scalene triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
