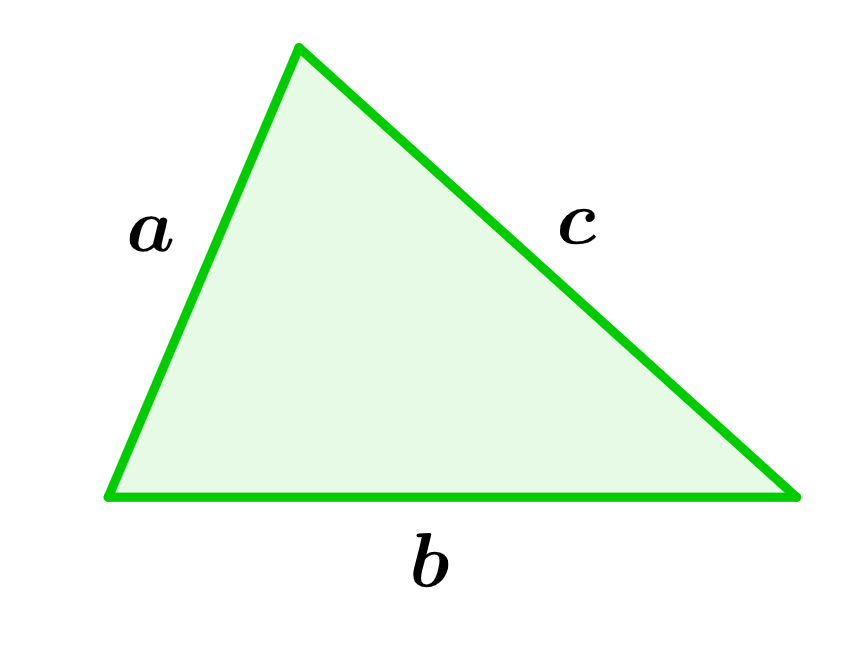
A scalene triangle has three sides of different lengths. We can calculate the area of this triangle using the length of the base and the height. Also, we can calculate its area using the lengths of the three sides. Finally, we can calculate the area if we know the length of its two sides and the angle between those sides.
Here, we will look at the formulas that we can use to calculate the area and the perimeter of a scalene triangle. Also, we will see some solved exercises in which we will apply these formulas.
What is the formula to find the perimeter of a scalene triangle?
To find the perimeter of a scalene triangle, we need to know the lengths of all the sides of the triangle. In a scalene triangle, the lengths of the three sides are different, so we can use different letters to represent each side. Therefore, knowing these lengths, the perimeter is the sum of all the lengths:
| $latex p=a+b+c$ |
where,
- $latex a=$ length of base
- $latex b=$ length of lateral side
- $latex c=$ length of opposite side
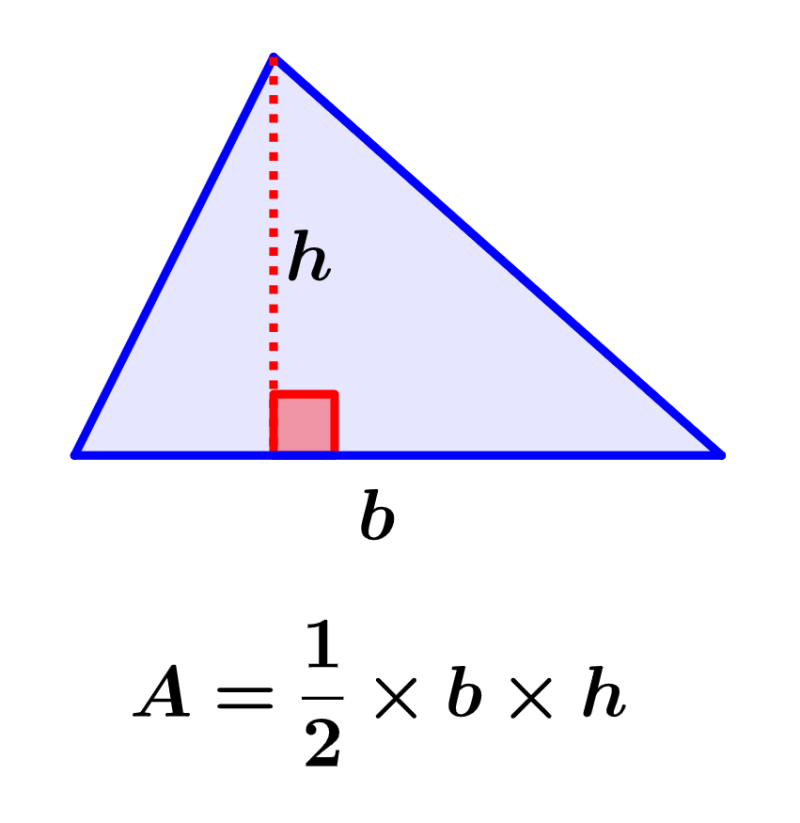
How to find the area of a scalene triangle?
To find the area of a scalene triangle, we need one of the following sets of measurements:
a) The length of one side and the perpendicular distance from that side to the opposite angle (the height).
b) The lengths of the three sides.
Area of the scalene triangle with base and height
To find the area of a scalene triangle if we know the length of its base and the corresponding height, we can use the following formula:
| $latex A=\frac{1}{2}\times b \times h$ |
where b is the length of the base and h is the length of the height.
Area of the scalene triangle without using the height
To find the area of the scalene triangle if we know the length of two sides and the measure of the angle between them, we can use the following formula:
| $latex A=\frac{ab}{2}\times \sin(C)$ |
where a and b are the lengths of two sides and C is the measurement of the angle between those sides.
Area of the scalene triangle with the length of the three sides
To find the length of a scalene triangle if we know the length of its three sides, we can use Heron’s formula:
| $latex A=\sqrt{S(S-a)(S-b)(S-c)}$ |
where, $latex a, ~b, ~c$ represent the lengths of the sides and S represents the semi perimeter that can be found with the following formula:
$latex S=\frac{a+b+c}{2}$
Area and perimeter of a scalene triangle – Examples with answers
EXAMPLE 1
What is the perimeter of a scalene triangle that has sides of lengths 6 m, 7 m, and 8 m?
Solution
We have the following lengths:
- Side 1, $latex a=6$ m
- Side 2, $latex b=7$ m
- Side 3, $latex c=8$ m
We can use the perimeter formula with these values:
$latex p=a+b+c$
$latex p=6+7+8$
$latex p=21$
The perimeter of the triangle is 21 m.
EXAMPLE 2
A scalene triangle has a base of 10 m and a height of 8 m. What is its area?
Solution
We can recognize the following values:
- Base, $latex b=10$ m
- Height, $latex h=8$ m
We use the first formula with these values:
$latex A=\frac{1}{2}\times b\times h$
$latex A=\frac{1}{2}\times 10\times 8$
$latex A=40$
The area is 40 m².
EXAMPLE 3
What is the perimeter of a scalene triangle with side lengths 11 m, 13 m, and 14 m?
Solution
We have the following sides:
- Side 1, $latex a=11$ m
- Side 2, $latex b=13$ m
- Side 3, $latex c=14$ m
We use these values with the perimeter formula:
$latex p=a+b+c$
$latex p=11+13+14$
$latex p=38$
The perimeter of the triangle is 38 m.
EXAMPLE 4
What is the area of a scalene triangle that has a base of 16 cm and a height of 18 cm?
Solution
We have the following information:
- Base, $latex b=16$ cm
- Height, $latex h=18$ cm
We substitute these values in the first formula:
$latex A=\frac{1}{2}\times b\times h$
$latex A=\frac{1}{2}\times 16\times 18$
$latex A=144$
The area is 144 cm².
EXAMPLE 5
A scalene triangle has sides of lengths 23 cm, 25 cm, and 31 cm. What is its perimeter?
Solution
We can identify the following:
- Side 1, $latex a=23$ cm
- Side 2, $latex b=25$ cm
- Side 3, $latex c=31$ cm
Therefore, we use these values in the formula:
$latex p=a+b+c$
$latex p=23+25+31$
$latex p=79$
The perimeter of the triangle is 79 cm.
EXAMPLE 6
The area of a scalene triangle is 84 m². If its base is 14 m, what is the length of its height?
Solution
We observe the following information:
- Area, $latex A=84$ m²
- Base, $latex b=14$ m
In this case, we want to find the height. Therefore, we use the first formula with these values and solve for h:
$latex A=\frac{1}{2}\times b\times h$
$latex 200=\frac{1}{2}\times (14)\times h$
$latex 84=7 h$
$latex h=12$
The length of the height is 12 m.
EXAMPLE 7
A scalene triangle has a perimeter of 86 m and sides of length 32 m and 28 m. What is the length of the third side?
Solution
We can observe the following information:
- Perimeter, $latex p=86$ m
- Side 1, $latex a=32$ m
- Side 2, $latex b=28$ m
We use these values in the perimeter formula and solve for c:
$latex p=a+b+c$
$latex 86=32+28+c$
$latex 86=60+c$
$latex c=26$
The third side has a length of 26 m.
EXAMPLE 8
A scalene triangle has sides of length 10 m, 12 m, and 14 m. Find the area.
Solution
In this case, we have the lengths of the three sides of the triangle:
- Side 1, $latex a=10$ m
- Side 2, $latex b=12$ m
- Side 3, $latex c=14$ m
We use Heron’s formula to find the area. For this, we start by finding the semi perimeter:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{10+12+14}{2}$
$latex S=\frac{36}{2}$
$latex S=18$
Therefore, we have:
$latex A=\sqrt{S(S-a)(S-b)(S-c)}$
$$A=\sqrt{18(18-10)(18-12)(18-14)}$$
$latex A=\sqrt{18(8)(6)(4)}$
$latex A=\sqrt{18(8)(6)(4)}$
$latex A=\sqrt{3456}$
$latex A=58.8$
The area is 58.8 m².
Area and perimeter of a scalene triangle – Practice problems
A triangle has two adjacent sides that measure 8 cm and 10 cm. If the angle between the sides is 30°, what is the area?
Write the answer in the input box.
See also
Interested in learning more about scalene triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
