Acute scalene triangles are scalene triangles in which all of their interior angles are acute. These triangles satisfy the definition of a scalene triangle and an obtuse triangle at the same time. Recall that an acute angle is an angle that is less than 90 degrees, and scalene triangles are triangles that have sides of different size and angles of different lengths.
Here, we will learn more details about acute scalene triangles. We will learn about their important characteristics and about their formulas. Also, we will solve some exercises using these formulas.
What are acute scalene triangles?
Acute scalene triangles are triangles that are both scalene and acute at the same time. This means that these triangles meet the conditions for a scalene triangle and an acute triangle. The scalene triangles have the condition of having all the sides of different lengths and all the angles of different measures.
In a scalene triangle, neither side is equal to another and no angle is equal to another. An acute triangle has the condition that all its internal angles are acute, that is, less than 90 degrees. The following is an example of an acute scalene triangle:
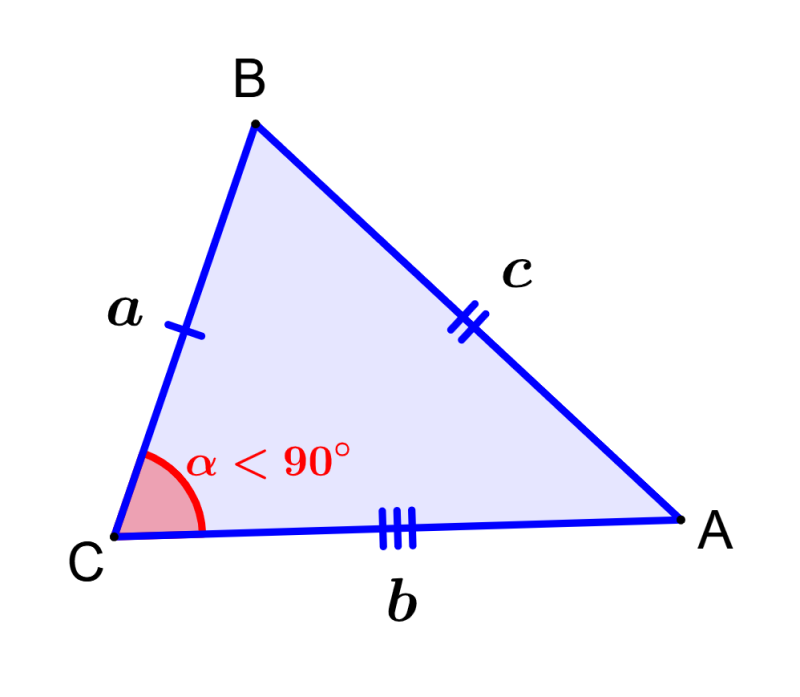
Formulas for acute scalene triangles
We can use the same formulas that we use with “normal” scalene triangles to solve acute scalene triangle problems.
Area of scalene triangles
The area of a scalene triangle is calculated using the lengths of the base and the height:
| $latex A=\frac{1}{2}\times b \times h$ |
Here, b is the length of the base and h represents the length of the height.
Perimeter of scalene triangles
If we know the length of the sides of the scalene triangle, its perimeter is simply the sum of the lengths:
| $latex p=a+b+c$ |
Here, $latex a, ~ b, ~ c$ are the side lengths of the acute scalene triangle.
Obtuse scalene triangles – Examples with answers
EXAMPLE 1
If a scalene triangle has a base of 20 m and a height of 22 m, what is its area?
Solution: We use the information given in the area formula:
$latex A=\frac{1}{2}\times b \times h$
$latex A=\frac{1}{2}\times 20 \times 22$
$latex A=220$
The area is 220 m².
EXAMPLE 2
A scalene triangle has sides of lengths 31 m, 33 m, and 34 m. What is its perimeter?
Solution: We use the perimeter formula with these lengths:
$latex p=a+b+c$
$latex p=31+33+34$
$latex p=98$
The perimeter is 98 m.
EXAMPLE 3
A scalene triangle has an area of 64 m² and its base is 20. What is the length of its height?
Solution: We use this information to substitute into the area formula and solve for h:
$latex A=\frac{1}{2}\times b\times h$
$latex 64=\frac{1}{2}\times 20\times h$
$latex 64=10h$
$latex h=6.4$
The height measures 6.4 m.
Acute scalene triangle – Practice problems
See also
Interested in learning more about scalene triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
