The hypotenuse of a right triangle is the side opposite the 90-degree angle. We can calculate the hypotenuse by using the Pythagorean theorem. This theorem tells us that the hypotenuse squared is equal to the sum of the squares of the lengths of the other two sides of the triangle. Therefore, to get the length of the hypotenuse, we need to have the lengths of the other sides.
Here, we will review the Pythagorean theorem. Also, we will use this theorem to solve some problems and find the length of the hypotenuse.
GEOMETRY
Relevant for…
Learning about the hypotenuse of a right triangle with examples.
GEOMETRY
Relevant for…
Learning about the hypotenuse of a right triangle with examples.
How to find the hypotenuse of a right triangle?
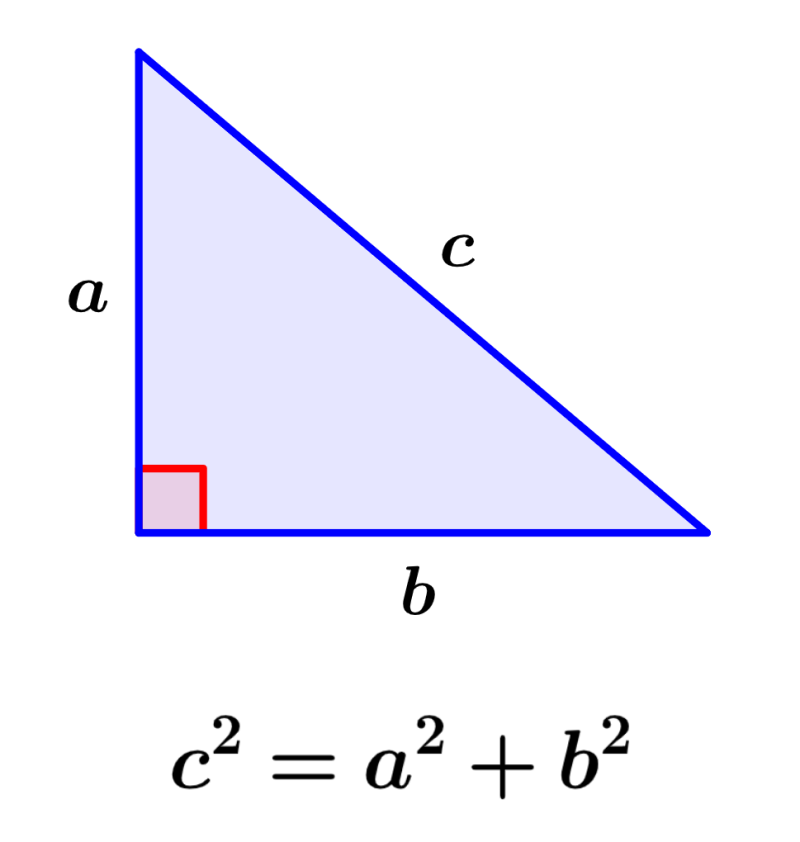
To find the hypotenuse of a right triangle, we use the Pythagorean theorem. Recall that the Pythagorean theorem tells us that the square of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. For example, let’s look at the following figure of a right triangle:
In this triangle, c is the hypotenuse since it is the side opposite the right angle. Therefore, the Pythagorean theorem tells us:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
where c is the length of the hypotenuse, a and b are the lengths of the other two sides.
Hypotenuse of a right triangle – Examples with answers
The Pythagorean theorem formula is used to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the exercises yourself to practice.
EXAMPLE 1
What is the length of the hypotenuse of a right triangle that has sides of length 3 m and 4 m?
Solution
We can recognize that we have sides $latex a=3$ and $latex b=4$. Therefore, we use the Pythagorean theorem with these values:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{3}^2}+{{4}^2}$
$latex {{c}^2}=9+16$
$latex {{c}^2}=25$
$latex c=5$
The length of the hypotenuse is 5 m.
EXAMPLE 2
We have a right triangle with sides of length 5 m and 12 m. What is its hypotenuse?
Solution
We have the side lengths $latex a=5$ and $latex b=12$. Therefore, we plug these values into the Pythagorean theorem:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{5}^2}+{{12}^2}$
$latex {{c}^2}=25+144$
$latex {{c}^2}=169$
$latex c=13$
The length of the hypotenuse is 13 m.
EXAMPLE 3
What is the hypotenuse of a right triangle with sides of length 9 m and 12 m?
Solution
We have the lengths $latex a=9$ and $latex b=12$. Therefore, we plug these values into the Pythagorean theorem:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{9}^2}+{{12}^2}$
$latex {{c}^2}=81+144$
$latex {{c}^2}=225$
$latex c=15$
The length of the hypotenuse is 15 m.
EXAMPLE 4
We have a right triangle with sides of length 10 m and 12 m. What is the length of its hypotenuse?
Solution
Here, we have the lengths $latex a=10$ and $latex b=12$. Therefore, we use these values in the Pythagorean theorem:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{10}^2}+{{12}^2}$
$latex {{c}^2}=100+144$
$latex {{c}^2}=244$
$latex c=15.62$
The length of the hypotenuse is 15.62 m.
EXAMPLE 5
What is the length of the hypotenuse of a right triangle that has sides of length 20 cm and 10 cm?
Solution
We can recognize that we have sides $latex a=20$ and $latex b=10$. Therefore, we use the Pythagorean theorem with these values:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{20}^2}+{{10}^2}$
$latex {{c}^2}=400+100$
$latex {{c}^2}=500$
$latex c=22.36$
The length of the hypotenuse is 22.36 cm.
Hypotenuse of a right triangle – Practice problems
Apply what you have learned about the Pythagorean Theorem to find the length of the hypotenuse of right triangles. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about right triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
