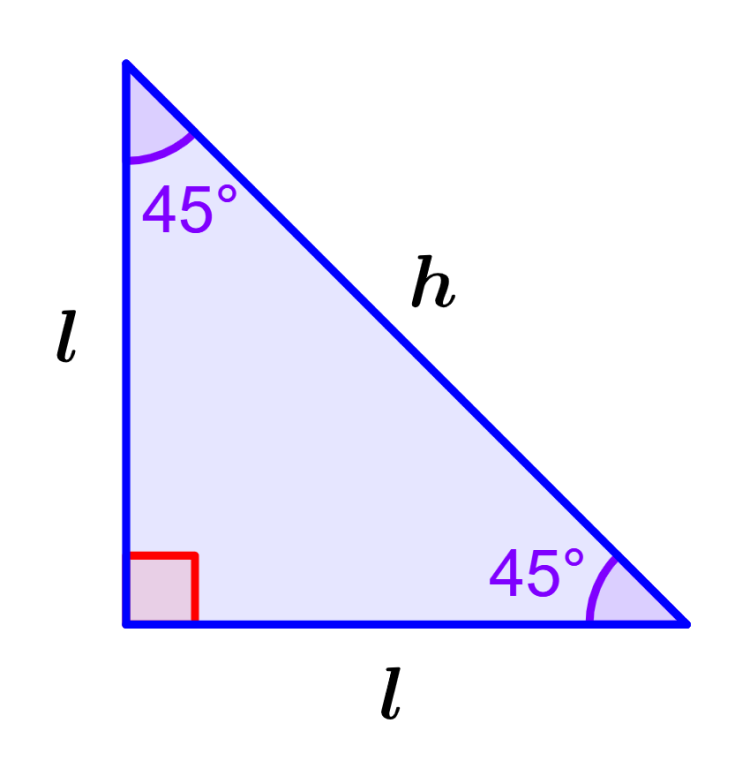
A right triangle is a triangle in which exactly one internal angle measures 90 degrees. Since the sum of the interior angles in any triangle is equal to 180 degrees, we know that the sum of the other two angles in a right triangle must equal 90 degrees. The two perpendicular sides are called the legs of a right triangle and the longest side, opposite the right angle, is called the hypotenuse. A right triangle can be scalene (which has three sides of different lengths) or isosceles (which has two sides of the same length).
In this article, we will look at the definition of an isosceles right triangle. Also, we will learn about its most important formulas and apply them to solve some problems.
Definition of isosceles right triangle
An isosceles right triangle is a 90-degree angle triangle consisting of two legs with equal lengths. Since the two legs have equal lengths, the corresponding angles will be congruent (the same measure). Therefore, in an isosceles right triangle, two legs and two acute angles are congruent.
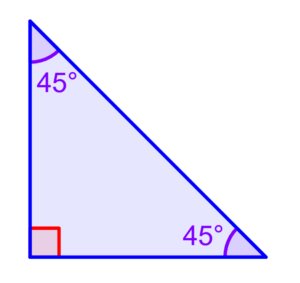
Since it is a triangle, the angle between the two legs will measure 90 degrees. Therefore, the legs will be perpendicular to each other.
Formulas for isosceles right triangles
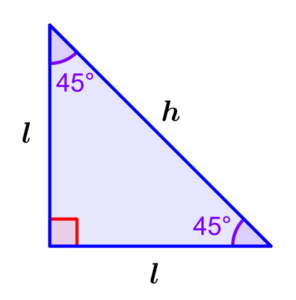
The most important formula associated with right triangles is the Pythagorean theorem. According to this theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides of the right triangle.
In the case of an isosceles right triangle, we know that the other two sides are equal in length. Therefore, we can find the hypotenuse using the following formula:
| $latex {{h}^2}={{l}^2}+{{l}^2}$ $latex {{h}^2}=2{{l}^2}$ |
where h is the length of the hypotenuse and l is the length of the sides.
Area of an isosceles right triangle
The area of any triangle can be calculated using the formula $latex A = \frac{1}{2}bh$, where b is the length of the triangle’s base and h is the length of the height. Since in an isosceles right triangle the sides have the same length, we can use l to represent the length of each side and we have the formula:
| $latex A= \frac{1}{2}l \times l$ $latex A= \frac{1}{2}{{l}^2}$ |
where l is the length of one of the congruent sides of the triangle.
Perimeter of an isosceles right triangle
The perimeter is equal to the sum of the lengths of all the sides of the triangle. Therefore, we can calculate the perimeter of a triangle using the formula $latex p =a+b+c$, where, $latex a, ~ b, ~ c$ are the lengths of the sides.
In an isosceles right triangle, we know that the sides have congruent lengths, so we have the following formula:
| $latex p=h+l+l$ $latex p=h+2l$ |
where h is the length of the hypotenuse and l is the length of the congruent sides.
Isosceles right triangles – Examples with answers
EXAMPLE 1
- What is the length of the hypotenuse of a triangle that has congruent sides of length 5 m?
Solution: We can use the Pythagorean theorem to find the hypotenuse. Since we have two congruent sides, we use the following formula:
$latex {{h}^2}=2{{l}^2}$
$latex {{h}^2}=2({{5}^2})$
$latex {{h}^2}=2(25)$
$latex {{h}^2}=50$
$latex h=7.07$
The length of the hypotenuse is 7.07 m.
EXAMPLE 2
- An isosceles right triangle has congruent sides of length 10 m. What is its area?
Solution: We use the modified formula of the area with the value $latex l=10$ that is the length of the congruent sides:
$latex A= \frac{1}{2}{{l}^2}$
$latex A= \frac{1}{2}({{10}^2})$
$latex A= \frac{1}{2}(100)$
$latex A=50$
The area of the triangle is 50 m².
EXAMPLE 3
- What is the perimeter of a triangle that has a hypotenuse of 19.8 m and congruent sides of length 14?
Solution: We can use the perimeter formula to solve this. We have two congruent sides, so we use the following formula:
$latex p=h+2l$
$latex p=19.8+2(14)$
$latex p=19.8+28$
$latex p=47.8$
The perimeter is 47.8 m.
Isosceles right triangle – Practice problems
See also
Interested in learning more about right triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
