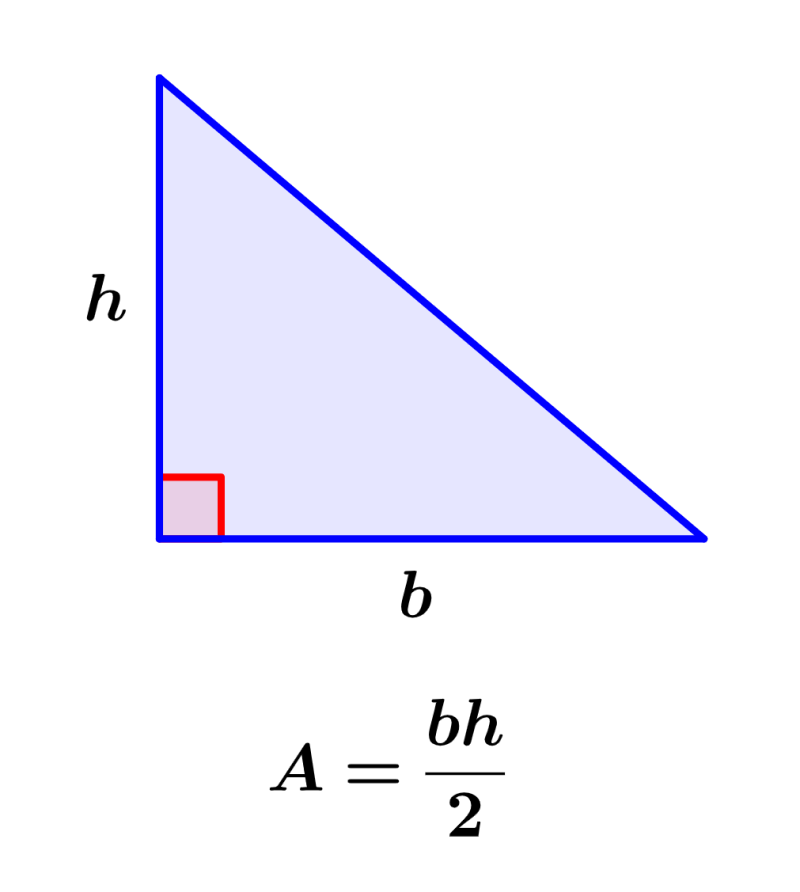
The area of a right triangle is the region covered by the 2D figure. Recall that a right triangle is a triangle that has a right angle, that is, a 90-degree angle. To calculate the area of these triangles, we can use the length of their base and the length of their height. Thus, we find the area by dividing the product of the height and the base by 2.
In this article, we will look at the formula for the area of a right triangle. In addition, we will use this formula to solve some problems.
Formula for the area of a right triangle
The area is a two-dimensional region and is measured in square units. The area can be defined as the amount of space taken up by the two-dimensional object.
The area of a right triangle can be calculated by using the following formula:
| $latex A= \frac{b \times h}{2}$ |
where b is the length of the triangle’s base and h is the length of the height.
Derivation of the area formula
We are going to derive the area of a right triangle using the following diagram:
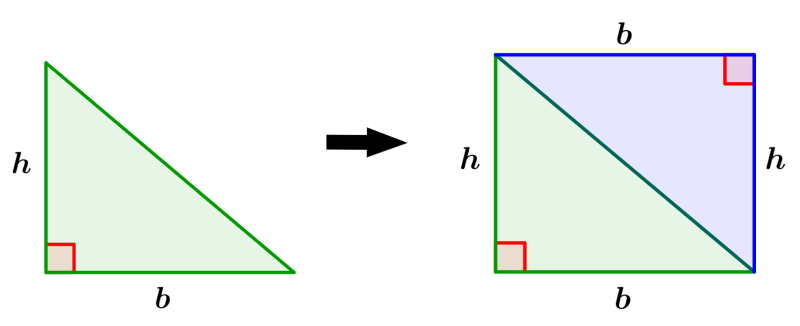
On the left side of the diagram, we have a right triangle. On the right side, we duplicate that triangle to form a rectangle. The height of the rectangle is equal to the height of the triangle and the base of the rectangle is also equal to the base of the triangle. Therefore, the area of the rectangle is:
$latex \text{Area}=\text{base}\times \text{height}$
$latex A=b\times h$
Therefore, the area of a right triangle will be half the area of a rectangle:
$latex A=\frac{b\times h}{2}$
Area of a right triangle – Examples with answers
The following examples for right triangles are solved using the formula above. Each example has its respective solution, but it is recommended that you try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
What is the area of a triangle that has a base of 8 m and a height of 10 m?
Solution
We have the following values:
- Height, $latex h=10$
- Base, $latex b=8$
Using these values in the formula, we have:
$latex A= \frac{bh}{2}$
$latex A=\frac{(8)(10)}{2}$
$latex A=\frac{80}{2}$
$latex A=40$
The area of the triangle is 40 m².
EXAMPLE 2
A triangle has a base of 16 m and a height of 10 m. What is its area?
Solution
We have the following information:
- Height, $latex h=10$ m
- Base, $latex b=16$ m
Substituting these values in the formula, we have:
$latex A= \frac{bh}{2}$
$latex A=\frac{(16)(10)}{2}$
$latex A=\frac{160}{2}$
$latex A=80$
The area of the triangle is 80 m².
EXAMPLE 3
The base of a right triangle is 15 m and its height is 11 m. What is its area?
Solution
We can identify the following information:
- Height, $latex h=11$ m
- Base, $latex b=16$ m
Using the area formula with these values, we have:
$latex A= \frac{bh}{2}$
$latex A=\frac{(15)(11)}{2}$
$latex A=\frac{165}{2}$
$latex A=82.5$
The area of the triangle is 82.5 m².
EXAMPLE 4
A right triangle has an area of 96 m² and a base of 8 m. What is its height?
Solution
In this case, we start with the area and we want to find the height. Therefore, we recognize the following values:
- Area, $latex A=96$ m²
- Base, $latex b=8$ m
We use these values in the formula and solve for h:
$latex A= \frac{bh}{2}$
$latex 96=\frac{8h}{2}$
$latex 192=8h$
$latex h=24$
The height of the triangle is 24 m.
EXAMPLE 5
A triangle has an area of 120 m² and a height of 20 m. What is the length of its base?
Solution
Again, we start with the area, but now we want to find the base. Therefore, we use the following values:
- Area, $latex A=120$ m²
- Base, $latex b=20$ m
We plug these values into the formula and solve for b:
$latex A= \frac{bh}{2}$
$latex 120=\frac{20b}{2}$
$latex 240=20b$
$latex b=12$
The base of the triangle is 12 m.
Area of a right triangle – Practice problems
Test your knowledge about the area of right triangles to solve the following problems. If you need help with this, you can look at the examples outlined above.
See also
Interested in learning more about right triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
