The orthocenter of a triangle can be found using two main methods. We can sketch the heights of the triangle and find the point of intersection. Alternatively, we can find the coordinates of the orthocenter algebraically.
In this article, we will learn how to find the orthocenter of a triangle using the two methods mentioned. Then, we will solve some practice problems.
What is the orthocenter of a triangle?
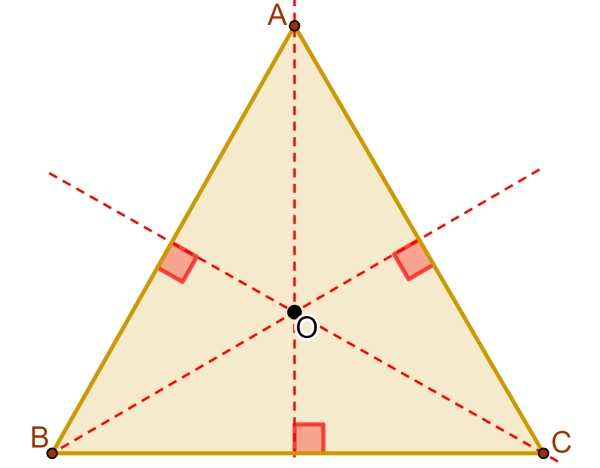
The orthocenter of a triangle is the point of intersection of the three heights of the triangle. In the diagram below, we can see that point O is the orthocenter:
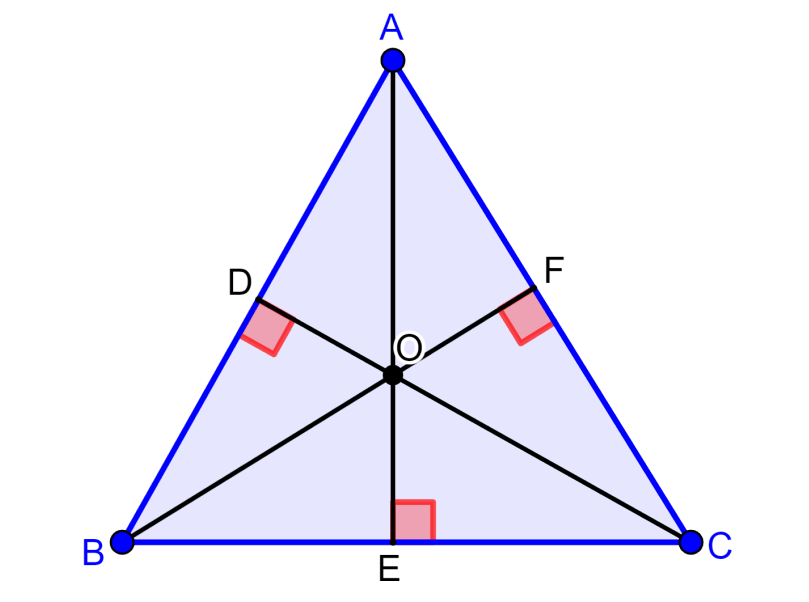
Remember that the heights of the triangle are the perpendicular segments that connect a vertex with its opposite side. Altitudes always form a 90° angle with the corresponding side.
Orthocenter of common triangles
Depending on the type of triangle we have, the location of the orthocenter varies.
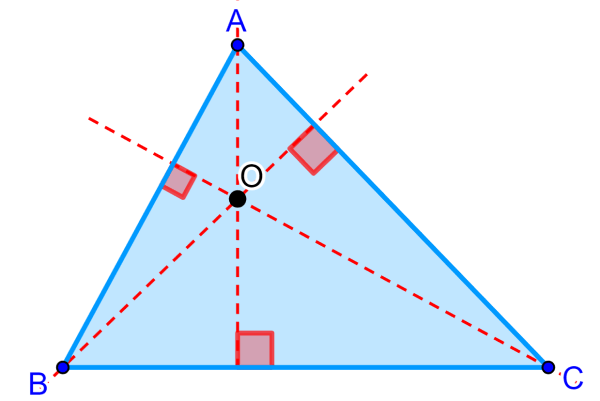
Orthocenter of an acute triangle
The orthocenter of all acute triangles always lies inside the triangle. Remember that an acute triangle is characterized in that all of its internal angles are less than 90°.
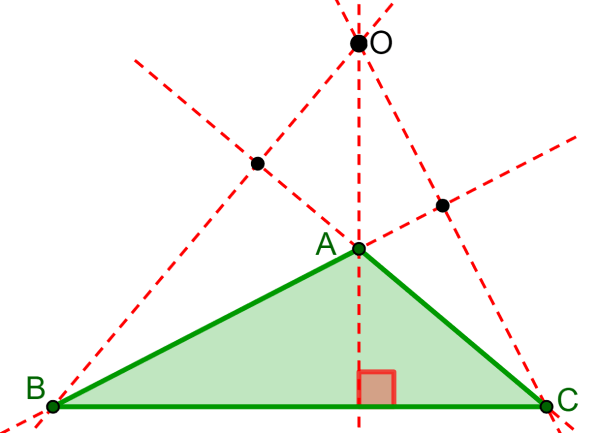
Orthocenter of an obtuse triangle
The orthocenter of all obtuse triangles always lies outside the triangle. Remember that an obtuse triangle is characterized by having an angle greater than 90°.
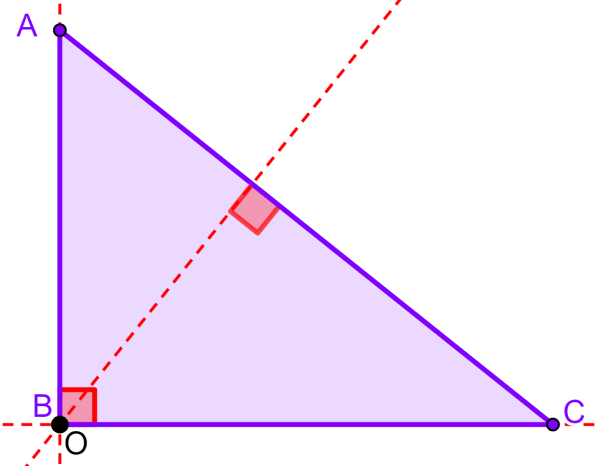
Orthocenter of a right triangle
The orthocenter of all right triangles is located at the central vertex of the right triangle. Remember that a right triangle has one 90° angle.
Orthocenter of an equilateral triangle
The orthocenter of all equilateral triangles is located in the same position as the centroid of the triangle. Remember that equilateral triangles have all three sides of the same length.
Finding the orthocenter of a triangle graphically
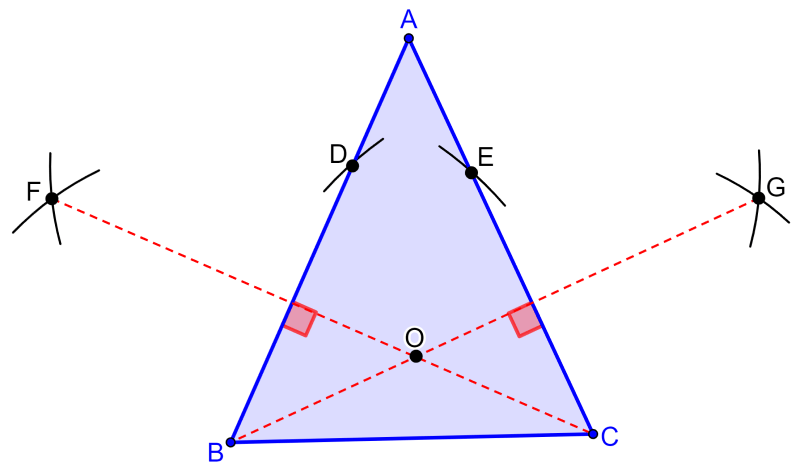
We can find the orthocenter of a triangle graphically by plotting two heights of the triangle and finding their point of intersection.
In turn, we can find the heights by drawing perpendicular lines from the vertices to opposite sides. We do this with the following steps:
Step 1: Using a radius equal to BC and centering on point B, draw an arc on side AC to get point E.
Step 2: Using a radius equal to BC and centering at point C, draw an arc on side AB to get point D.
Step 3: Using a radius equal to BD, draw intersecting arcs from B and D to form point F and draw segment CF.
Step 4: Using a radius equal to CE, draw intersecting arcs from C and E to form point G and draw segment BG.
Step 5: Mark the point of intersection of segments CF and BG.
Segments CF and BG are perpendicular to sides AB and AC respectively. This means that they represent the heights of the triangle. Therefore, the point of intersection is the orthocenter of the triangle.
Finding the orthocenter of a triangle algebraically
The orthocenter of a triangle can be found algebraically using the coordinates of the vertices of the triangle. We can follow the process using the following triangle.
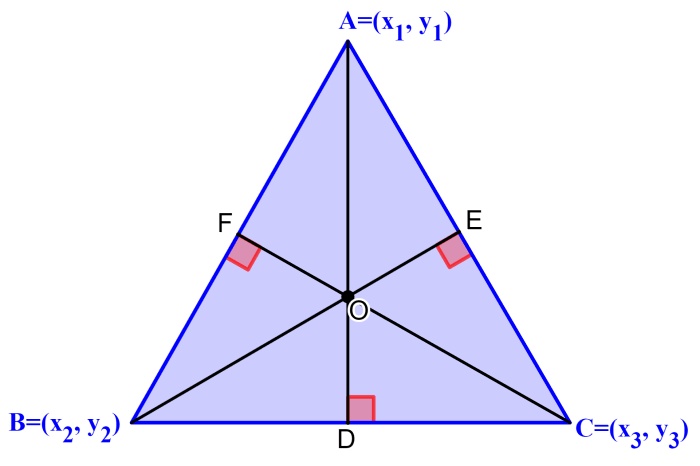
In this triangle, $latex A(x_{1},~y_{1})$, $latex B(x_{2},~y_{2})$, $latex C(x_{3},~y_{3})$ are the vertices and AD , BE and CF are the heights. Point O is the orthocenter since it is the point of intersection.
Step 1: To find the heights, we have to start by finding the slopes of the sides of the triangle. For this, we use the slope formula:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Representing the slope of line AC as $latex m_{AC}$, we have:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
Similarly, we also have:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
Step 2: Once we have the slopes of the sides, we can find the slopes of the heights by considering that the heights are perpendicular to the sides. The slope of a line perpendicular to another line is:
perpendicular line $latex =-\frac{1}{m}$
where m is the slope of the original line.
Therefore, the slopes of the heights are:
Slope of BE: $latex m_{BE}=-\frac{1}{m_{AC}}$
Slope of AD: $latex m_{AD}=-\frac{1}{m_{BC}}$
Step 3: We can find the equations of the lines that go through BE and AD using the point-slope form. Then, we have:
$latex m_{BE}=\frac{y-y_{2}}{x-x_{2}}$
$latex m_{AD}=\frac{y-y_{1}}{x-x_{1}}$
Step 4: Since we know the values of $latex (x_{1},~y_{1})$ and $latex (x_{2},~y_{2})$, we can use any method to solve the system of equations and find the values of x and y, which are the coordinates of the orthocenter.
Orthocenter of a triangle – Examples with answers
In the following examples, we can see how to find the coordinates of the orthocenter of a triangle algebraically.
EXAMPLE 1
If a triangle has vertices A(5, 7), B(2, 3), and C(6, 4), find the slopes of its sides.
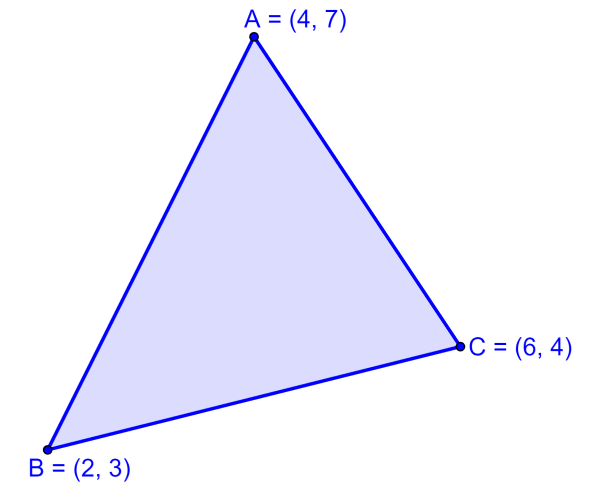
Solution: We have the following coordinates:
- $latex (x_{1},~y_{1})=(5, ~7)$
- $latex (x_{2},~y_{2})=(2,~3)$
- $latex (x_{3},~y_{3})=(6,~4)$
Slope of AC:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
$latex m_{AC}=\frac{4-7}{6-5}$
$latex m_{AC}=-3$
Slope of BA:
$latex m_{BA}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$
$latex m_{BA}=\frac{7-3}{5-2}$
$latex m_{BA}=\frac{4}{3}$
Slope of BC:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
$latex m_{BC}=\frac{4-3}{6-2}$
$latex m_{BC}=\frac{1}{4}$
EXAMPLE 2
Use the slopes found in Example 1 to determine the coordinates of the orthocenter of the triangle.
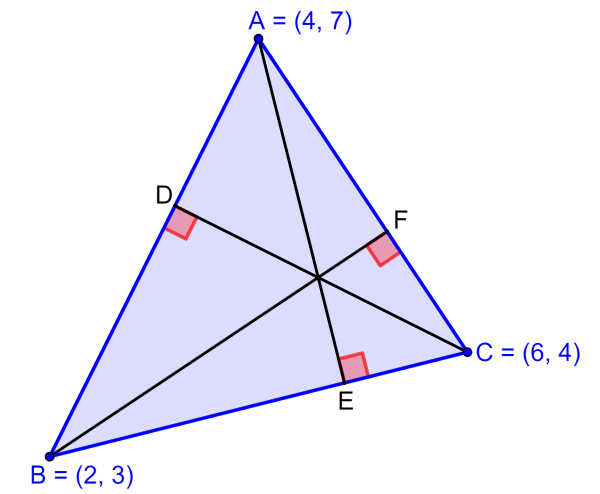
Solution: We have to find the slopes of the lines perpendicular to the sides since they correspond to the heights of the triangle. Therefore, we have:
- $latex m_{AE}=$ perpendicular to BC
- $latex m_{BF}=$ perpendicular to AC
- $latex m_{CD}=$ perpendicular to AB
The slope of a perpendicular line is equal to $latex -\frac{1}{m}$, where, m is the slope of the original line, we have:
$latex m_{AE}=-4$
$latex m_{BF}=\frac{1}{3}$
$latex m_{CD}=-\frac{3}{4}$
Using the point-slope form, $latex y-y_{1}=m(x-x_{1})$, we can find the equations of the perpendicular lines. We only need two equations to find the point of intersection.
We use the slope of CD and the point C=(6, 4) to find the first equation:
$latex y-4=-\frac{3}{4}(x-6)$
$latex 4(y-4)=-3(x-6)$
$latex 4y-16=-3x+18$
$latex 3x+4y=34$
Now, we use the slope of BF and the point B=(2, 3) to find the second equation:
$latex y-3=\frac{1}{3}(x-2)$
$latex 3(y-3)=x-2$
$latex 3y-9=x-2$
$latex -x+3y=7$
Any method can be used to solve the system of two equations and we find the solution $latex x=\frac{74}{18},~ y=\frac{55}{13}$.
This solution represents the point of intersection of the lines. Therefore, the coordinates of the orthocenter are $latex (\frac{74}{18},~\frac{55}{13})$.
Orthocenter of a triangle – Practice problems
Solve the following practice problems using the algebraic method to find the coordinates of the orthocenter.
See also
Interested in learning more about the incenter, orthocenter, centroid, and circumcenter of a triangle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
