The centroid of a triangle can be found using an algebraic method or using a graphical method. To find the centroid algebraically, we have to use a formula and the coordinates of the vertices of the triangle. To find the centroid graphically, we have to draw two medians of the triangle.
In this article, we will learn how to find the centroid of a triangle using the two methods listed. Then, we will solve some practice problems.
What is the centroid of a triangle?
The centroid of a triangle is the point of intersection of the three medians of the triangle. In the diagram below, we can see that the red dot is the centroid:
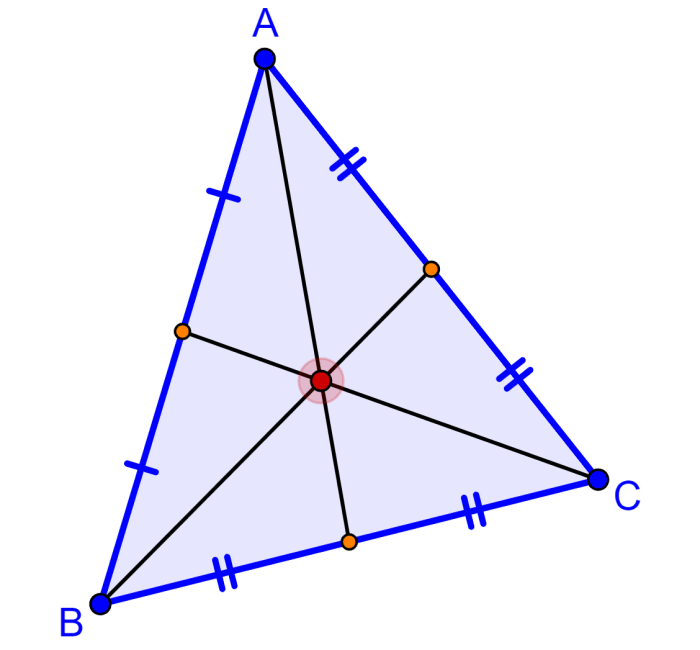
Remember that the medians of the triangle are the segments that connect a vertex with the midpoint of its opposite side. This means that the centroid is the geometric center of the triangle.
Properties of the centroid of a triangle
The following are some of the important properties and characteristics of the centroid of a triangle:
- The centroid of a triangle is the point of intersection of the medians of the triangle.
- The centroid represents the geometric center of the triangle.
- The centroid of a triangle is always located inside the triangle.
- The centroid of an equilateral triangle is located in the same position as its incenter, orthocenter, and circumcenter.
- The centroid divides the medians in a 2:1 ratio.
Finding the centroid of a triangle graphically
The centroid of a triangle can be found graphically by sketching the medians of the triangle and determining their point of intersection.
In turn, we can find the medians by finding the midpoint of each side and drawing a line segment from that point to the opposite vertex. We do this with the following steps:
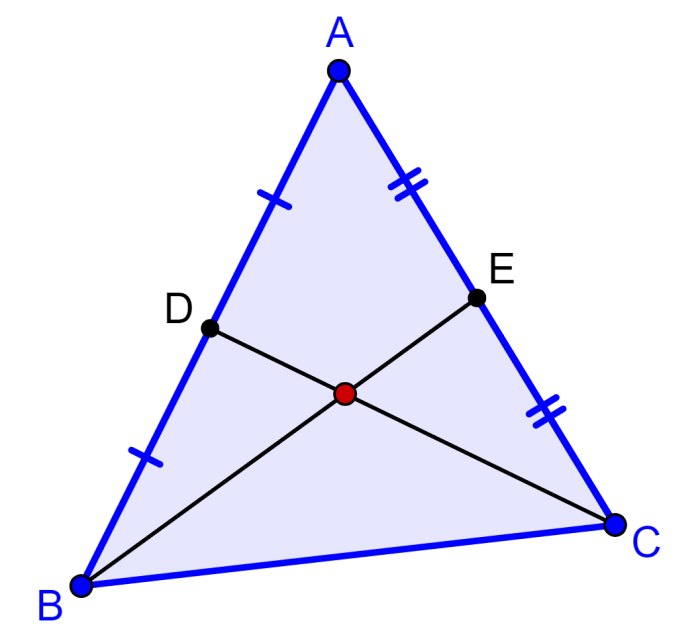
Step 1: Measure the length of side AB and mark its midpoint to obtain point D.
Step 2: Draw a line segment from vertex C to point D.
Step 3: Measure the length of side AC and mark its midpoint to obtain point E.
Step 4: Draw a line segment from vertex B to point E.
Step 5: Mark the point of intersection of segments AB and AC.
The segments AB and AC are the medians of the triangle. This means that the point of intersection is the centroid of the triangle.
Finding the centroid of a triangle algebraically
The centroid of a triangle can be found algebraically if we know the coordinates of the vertices of the triangle. We can follow the process using the following triangle.
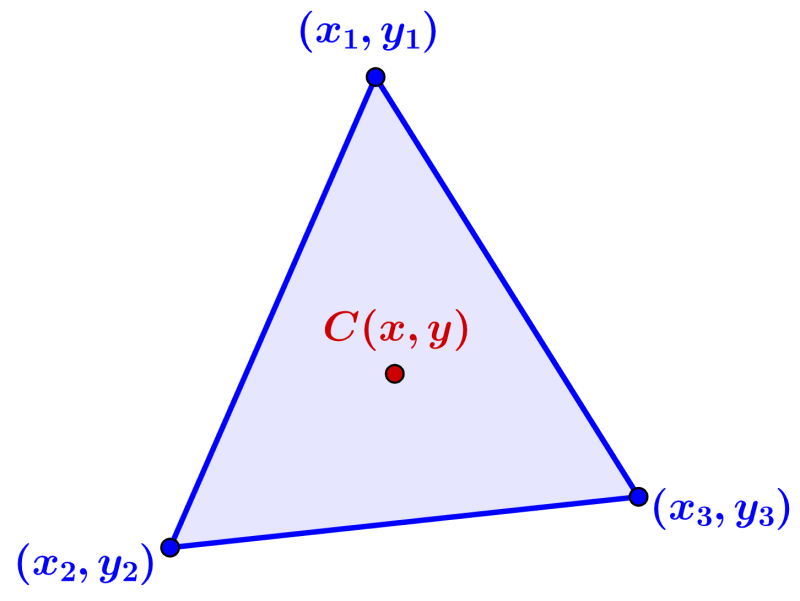
In this triangle, $latex (x_{1},~y_{1})$, $latex (x_{2},~y_{2})$, $latex (x_{3},~y_{3})$ are the vertices and the point C(x, y) is the centroid of the triangle.
Then, we use the following formula:
$latex C(x, y)=\left( \frac{x_{1}+x_{2}+x_{3}}{3},\frac{y_{1}+y_{2}+y_{3}}{3}\right)$
Basically, we have to add the x-coordinates of the vertices and divide the sum by 3 to get the x-coordinate of the centroid. Similarly, we add the y-coordinates of the vertices and divide the sum by 3 to get the y-coordinate of the centroid.
Centroid of a triangle – Examples with answers
In the following examples, we apply the algebraic method to find the centroid of the triangles.
EXAMPLE 1
What are the coordinates of the centroid of a triangle that has vertices A(3, 6), B(1, 1), and C(5, 2)?
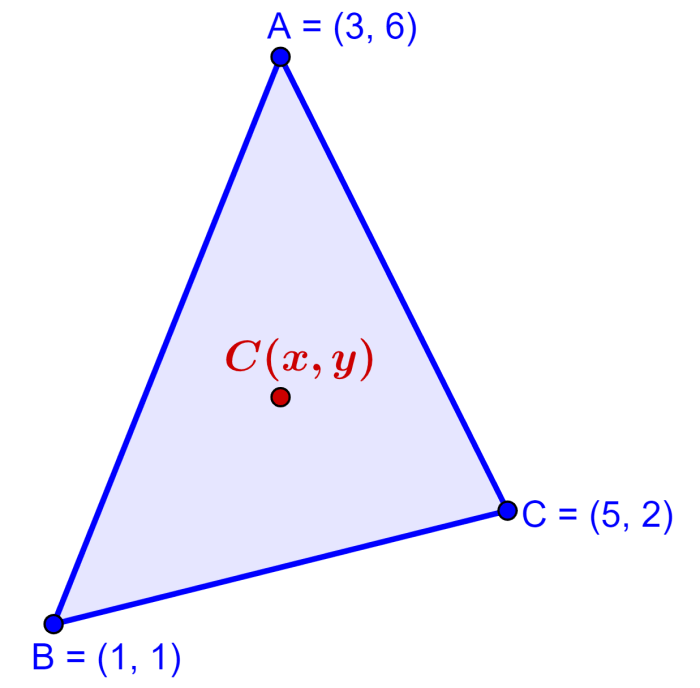
Solution: We have to use the centroid formula with the following coordinates:
- $latex (x_{1},~y_{1})=(3, ~6)$
- $latex (x_{2},~y_{2})=(1,~1)$
- $latex (x_{3},~y_{3})=(5,~2)$
Therefore, we have:
$latex C(x, y)=\left(\frac{x_{1}+x_{2}+x_{3}}{3},~\frac{y_{1}+y_{2}+y_{3}}{3}\right)$
$latex C(x, y)=\left(\frac{3+1+5}{3},~\frac{6+1+2}{3}\right)$
$latex C(x, y)=\left(\frac{9}{3},~\frac{9}{3}\right)$
$latex C(x, y)=(3,~3)$
EXAMPLE 2
What are the coordinates of the centroid of a triangle that has vertices A(5, 7), B(2, 3), and C(6, 4)?
Solution: We have the following coordinates:
- $latex (x_{1},~y_{1})=(5, ~7)$
- $latex (x_{2},~y_{2})=(2,~3)$
- $latex (x_{3},~y_{3})=(6,~4)$
Then, using the centroid formula, we have:
$latex C(x, y)=\left(\frac{x_{1}+x_{2}+x_{3}}{3},~\frac{y_{1}+y_{2}+y_{3}}{3}\right)$
$latex C(x, y)=\left(\frac{5+2+6}{3},~\frac{7+3+4}{3}\right)$
$latex C(x, y)=\left(\frac{13}{3},~\frac{14}{3}\right)$
Centroid of a triangle – Practice problems
Solve the following practice problems using the algebraic method to find the coordinates of the centroid.
See also
Interested in learning more about the incenter, orthocenter, centroid, and circumcenter of a triangle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
