The incenter of a triangle can be found by sketching the angle bisectors of the triangle and finding their point of intersection. In addition, we can also calculate the coordinates of the incenter using a formula with the coordinates of the vertices and the lengths of the sides of the triangle.
In this article, we will learn how to find the incenter of a triangle using a graphical method and an algebraic method. Then, we will solve some practice problems.
What is the incenter of a triangle?
The incenter of a triangle is the point of intersection of the three bisectors of the triangle. In turn, the bisectors are the segments that divide the angles in half as we can see in the diagram:
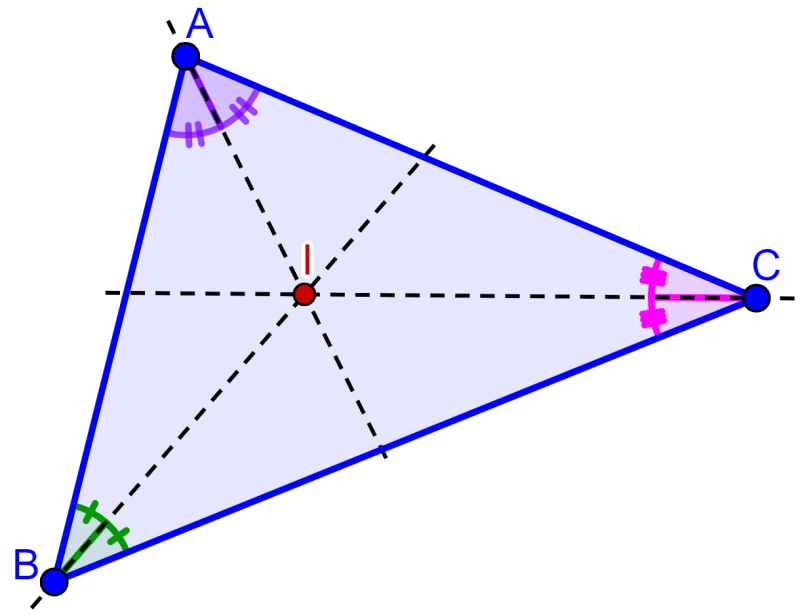
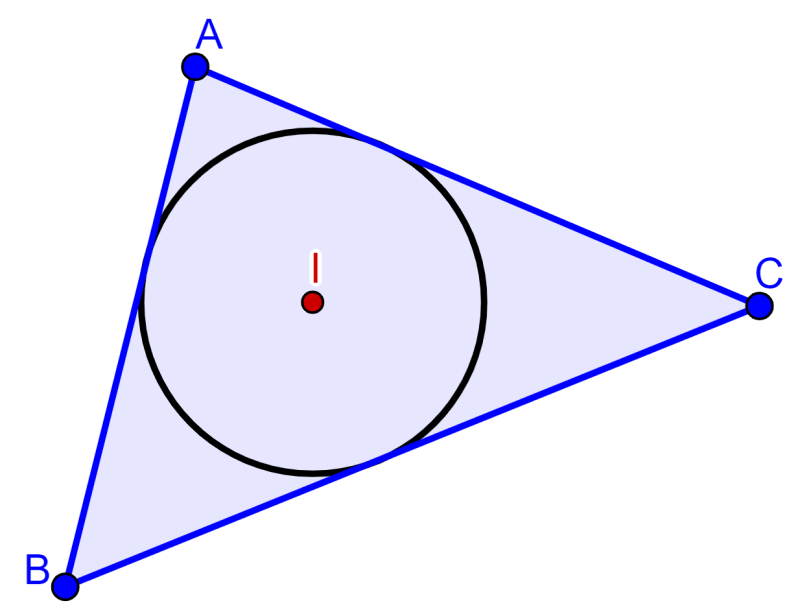
Alternatively, we can define the incenter of a triangle as the center of a circle inscribed in the triangle. In turn, an inscribed circle is the largest circle that fits inside the triangle.
Properties of the incenter of a triangle
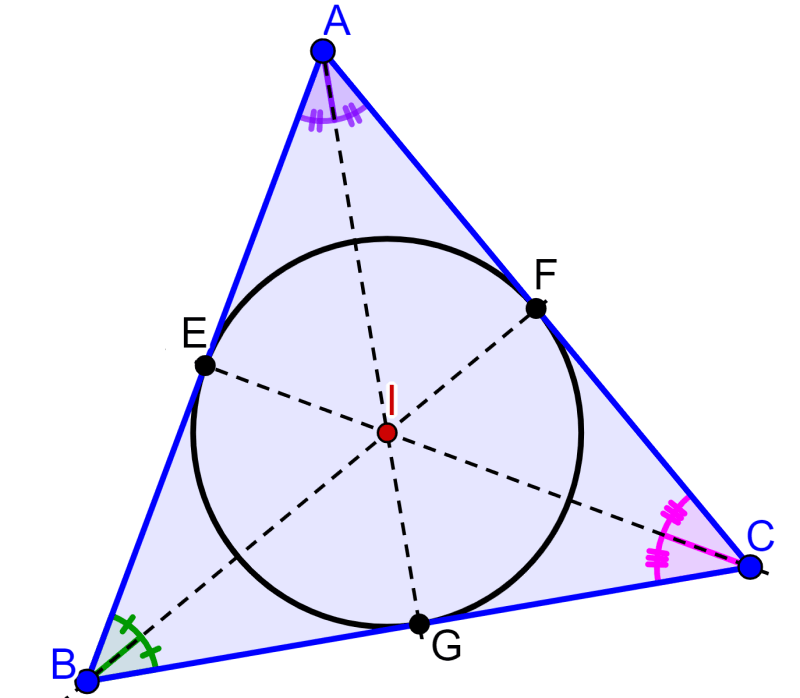
Property 1: The incenter of a triangle is always located inside the triangle no matter what type of triangle we have.
Property 2: If I is the incenter of the triangle, then segments AE and AF must have the same length. The same happens with the segments BE and BG, and with the segments CG and CF.
Property 3: If I is the incenter of the triangle, then the angles ∠ABI and ∠CBI are equal. The same happens with the angles ∠BAI and ∠CAI, and with the angles ∠ACI and ∠BCI.
Property 4: The sides of the triangle are tangent to the inscribed circle, so IE, IF and IG are equal to the radius of the circle and are called the inradius.
Property 5: The area of the triangle can be calculated using the formula A=sr, where r is the inradius of the triangle and s is the semi perimeter. In turn, the semi perimeter is $latex s=\frac{a+b+c}{2}$.
Finding the incenter of a triangle graphically
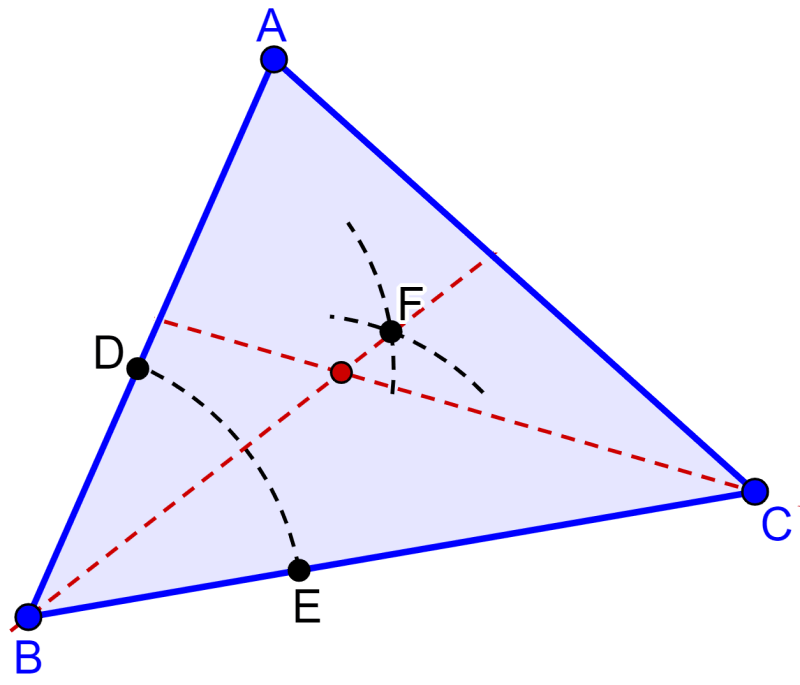
We can find the incenter of a triangle graphically by drawing the angle bisectors and finding the point of intersection. Therefore, we follow the following steps using a compass:
Step 1: Center the compass at vertex B and using any radius, draw an arc that cuts both sides of the triangle. Therefore, we get points D and E.
Step 2: With the same radius, center the compass at points D and E to draw two arcs to get the point of intersection F.
Step 3: Draw a segment that passes through points B and F. That segment is the bisector of angle B.
Step 4: By repeating the same process using another vertex of the triangle, we can draw another bisector.
Step 5: Find the point of intersection of two bisectors.
The point of intersection represents the incenter of the triangle.
Finding the incenter of a triangle algebraically
The coordinates of the incenter of the triangle can be obtained algebraically using a formula. However, we need to know the coordinates of all three vertices and the lengths of all three sides.
Suppose we have the following triangle:
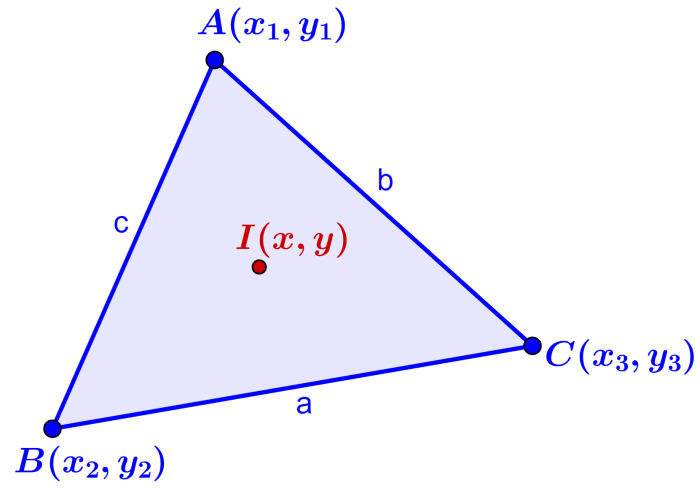
Then, we can calculate the incenter using the following formula:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
where, $latex A(x_{1},~y_{1})$, $latex B(x_{2},~y_{2})$ and $latex C(x_{3},~y_{3})$ are the coordinates of the three vertices of the triangle and a, b, c are the sides opposite each vertex.
Incenter of a triangle – Examples with answers
In the following examples, we can see how to find the coordinates of the incenter of a triangle algebraically.
EXAMPLE 1
I represents the incenter of the following triangle. What is the size of angle x?
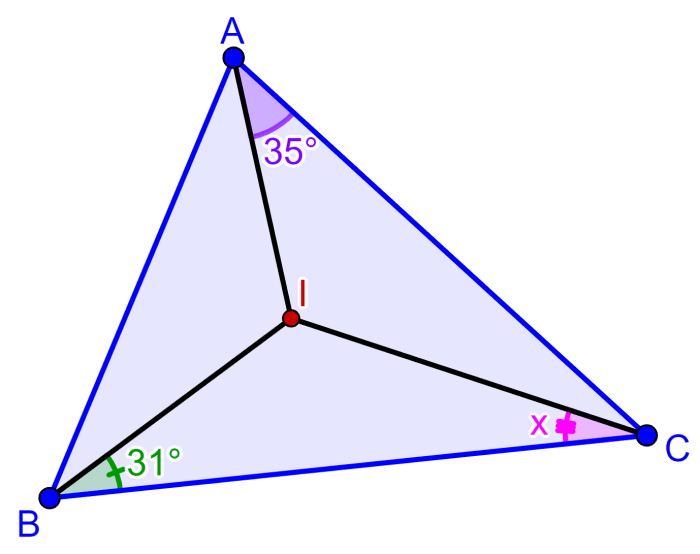
Solution: Since I is the incenter of the triangle, the segments connecting the incenter to the vertices are bisectors, so they divide the angles into two equal parts.
This means that the three interior angles of the triangle are:
2×35°=70°
2×31°=62°
2×x=2x
A triangle always has a sum of interior angles equal to 180°, so we have:
70°+62°+2x=180°
2x=180°-70°-62°
2x=48°
x=24°
EXAMPLE 2
A triangle has an area of 15 m² and its perimeter is equal to 18 m. What is the radius of the circle inscribed in the triangle?
Solution: We have the following information:
- Triangle area = 15 u²
- Triangle perimeter = 18 u
The area of a triangle can be calculated using A=sr, where s is the semi perimeter and r is the inradius. The semi perimeter is half the perimeter. Therefore, we have:
A=sr
15=9r
r=1.67
Thus, the radius of the inscribed circle is 1.67 m.
EXAMPLE 3
The triangle below has the vertices A(0, 4), B(0, 1), and C(4, 4). What are the coordinates of its incenter?
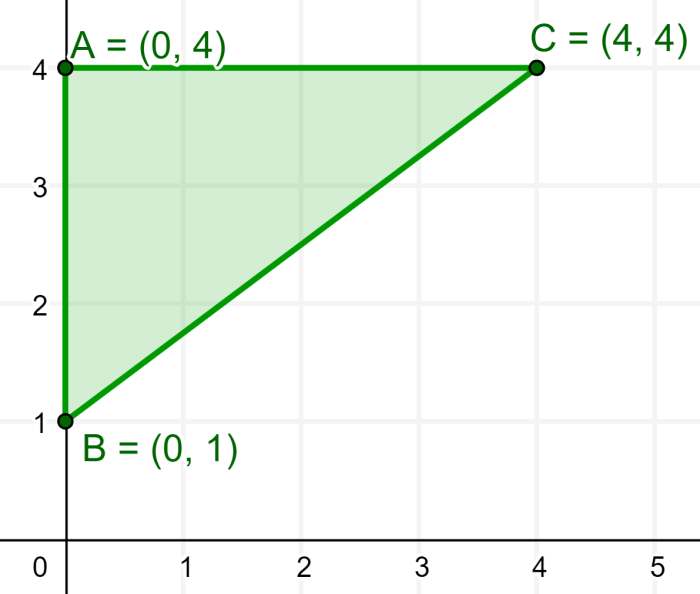
Solution: We can use the incenter formula along with the coordinates of the vertices and the lengths of the sides.
Using the diagram, we can see that the length of b is 4 units and the length of c is 3 units. Therefore, we use the Pythagorean theorem with those two sides to find the length of a:
a²=b²+c²
a²=4²+3²
a²=16+9
a²=25
a=5
Using the incenter formula, we have:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
$$=\left(\frac{0+0+3(4)}{5+4+3},~\frac{5(4)+4(1)+3(4)}{5+4+3}\right)$$
$latex =(\frac{12}{12},~\frac{36}{12})$
$latex =(1,~3)$
The coordinates of the incenter are (1, 3).
Incenter of a triangle – Practice problems
Solve the following practice problems using the algebraic method to find the coordinates of the incenter.
See also
Interested in learning more about the incenter, orthocenter, centroid, and circumcenter of a triangle? Take a look at these pages:



