The slope-intercept form of a line is one of the most commonly used forms to find the equation of a line. When we know the y-intercept (b) and the slope of the line (m), we can use the form y = mx+b. The equation of the line satisfies any point that is located on the line.
In this article, we will learn everything related to the slope-intercept form of a line. We will learn how to derive its formula and apply it to solve some practice problems.
GEOMETRY
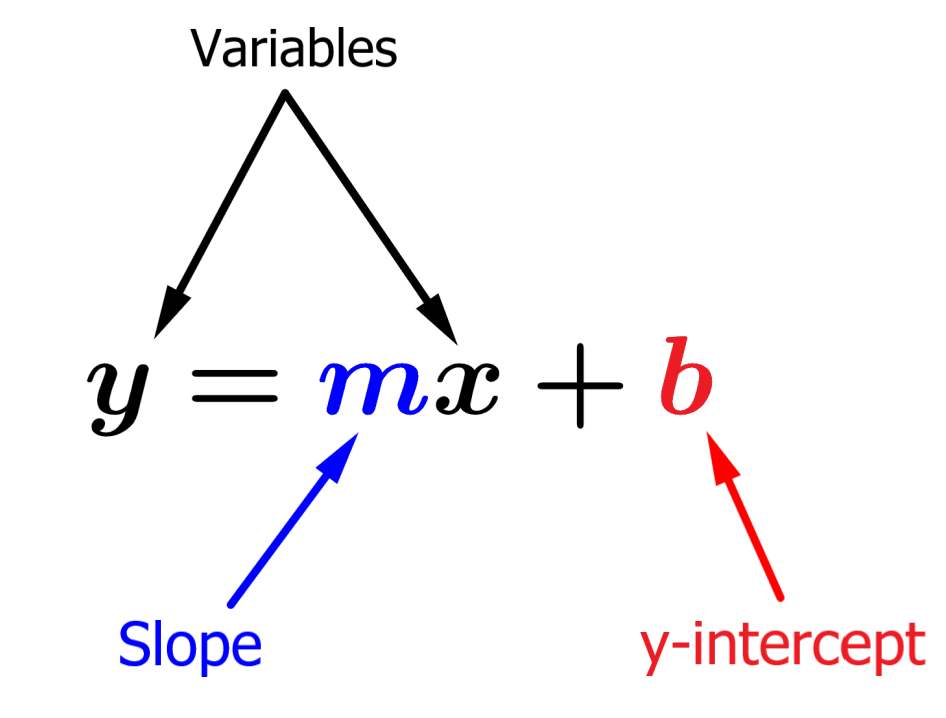
Relevant for…
Learning to find the equation of a line using slope-intercept form.
GEOMETRY
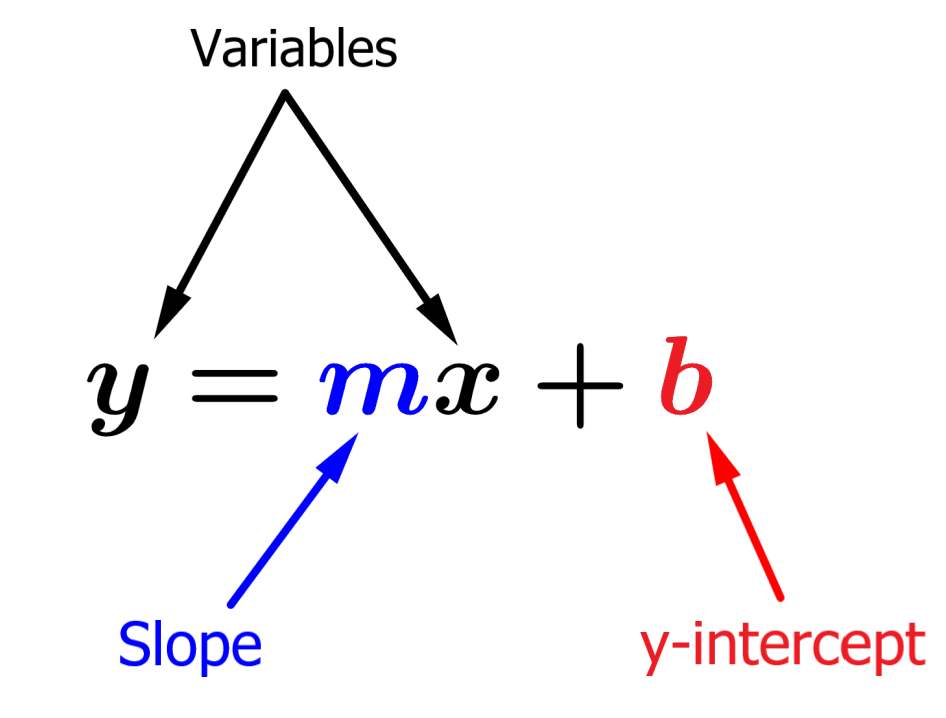
Relevant for…
Learning to find the equation of a line using slope-intercept form.
Formula for the slope-intercept form of a line
There are different methods that we can use to determine the equation of a line in the Cartesian plane. Everything will depend on the information we have available.
If we know the y-intercept and the slope of the line, we can use the slope-intercept form: y = mx+b.
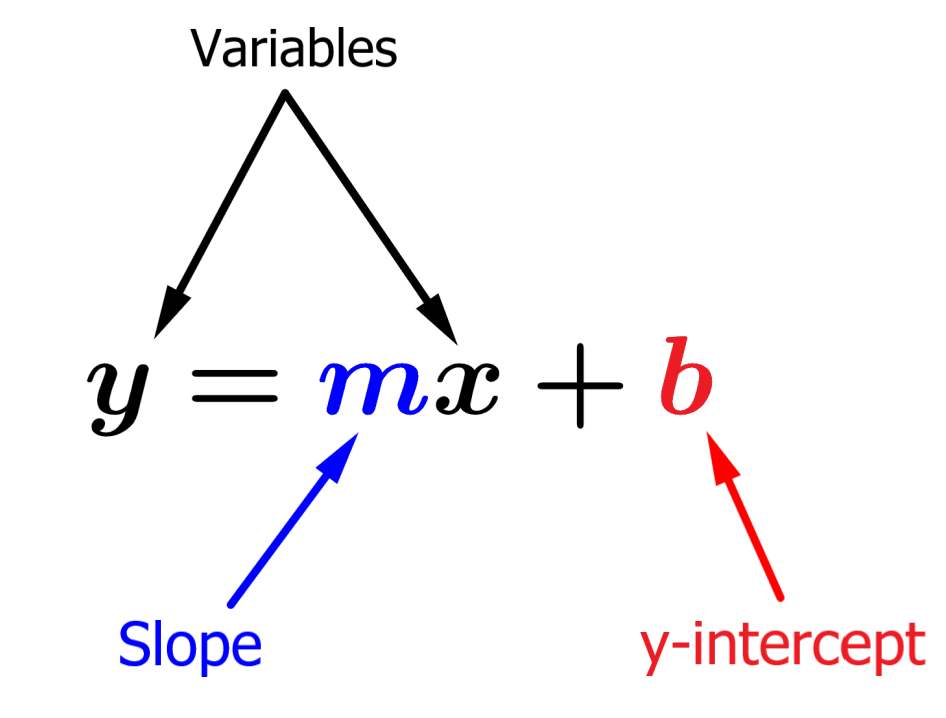
The y-intercept is the y-coordinate where the line intersects the y-axis. The y-intercept is represented by the letter b and is commonly given in the form (0, b).
The slope of a line represents the change in the y-coordinates with respect to the x-coordinates. A positive slope indicates that the line increases from left to right, and a negative slope indicates that the line decreases from left to right.
The variables x and y remain the same when we use the slope-intercept form formula, since (x, y) represents all points that lie on the line.
Proof of the formula for the point-slope form of a line
To prove the formula for the point-slope form of a line, we are going to use the following graph:
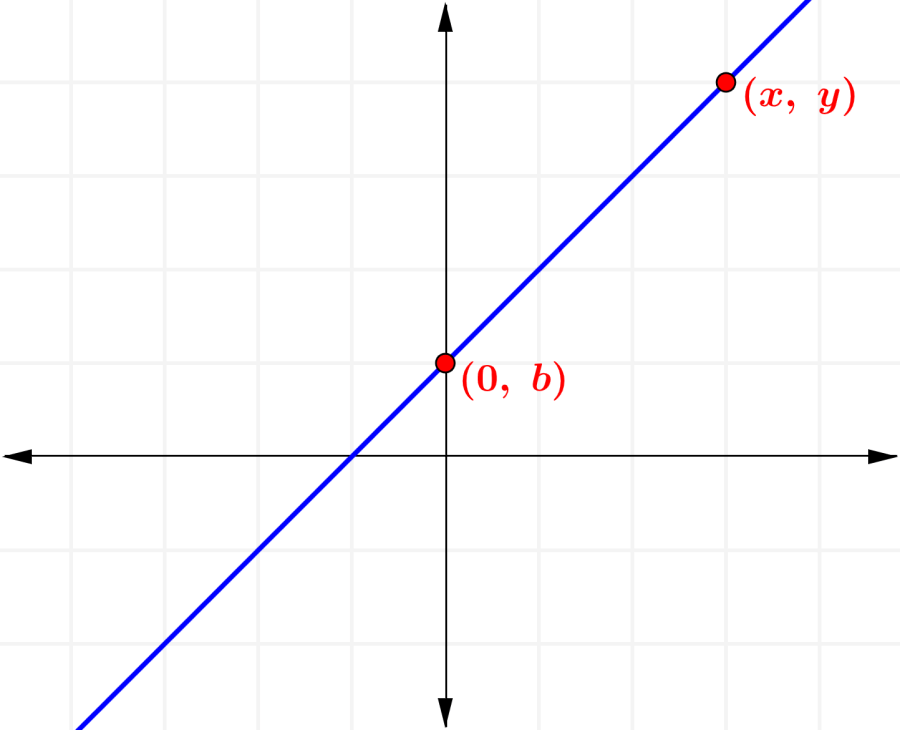
Here, we have a line that has a slope equal to m and that intersects the y-axis at the point (0, b). In addition, we consider the point (x, y), which is an arbitrary point that lies on the line.
Now, since the points (0, b) and (x, y) are just two points on the line, we can write as follows:
$latex (x_{1},~y_{1})=(0,~b)$
$latex (x_{2},~y_{2})=(x,~y)$
Let’s recall that the Formula for the Slope of a Line using two points is as follows:
$$m=\frac{(y_{2}-y_{1}}{x_{2}-x_{1}}$$
Therefore, if we use this formula to find the slope of the line above, we have:
$$m=\frac{(y-b)}{(x-0)}$$
$$m=\frac{(y-b)}{x}$$
We can solve this equation for y:
$$m=\frac{(y-b)}{x}$$
$latex mx=y-b$
$latex y=mx+b$
Therefore, we have derived the formula for the slope-intercept form of a line.
Slope-intercept form of a line – Examples with answers
The following problems are solved by applying the slope-intercept form of a line. Each example has its respective solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the equation of a line that has a slope of 1/2 and its y-intercept is (0, -2).
Solution
To find the equation of the line, we use slope-intercept form with the following information:
- m = 1/2
- b = -2
$latex y=mx+b$
$latex y=\frac{1}{2}x-2$
The equation of the given line is $latex y=\frac{1}{2}x-2$.
EXAMPLE 2
What is the equation of a line that has a slope of -2 and a y-intercept of (0, 3)?
Solution
We apply the formula of the slope-intercept form with the following information:
- m = -2
- b = 3
$latex y=mx+b$
$latex y=-2x+3$
La ecuación de la recta dada es $latex y=-2x+3$.
EXAMPLE 3
What is the equation of a horizontal line that has a y-intersect at (0, -5)?
Solution
In this case, we do not have the slope given explicitly. However, the line is indicated to be horizontal, and we know that a horizontal line has no change in the y-axis, so its slope equals 0.
Therefore, we have the following information:
- m = 0
- b = -5
Using slope-intercept form, we have:
$latex y=mx+b$
$latex y=0x-5$
$latex y=-5$
The equation of the horizontal line is $latex y=-5$. On a horizontal line, the y values remain constant.
EXAMPLE 4
Determine the equation of a line that is parallel to the line y = 5x+2 and has a y-intercept at (0, -3).
Solution
In this example, we also do not have the slope of the line given explicitly. However, we have that the line is parallel to y = 5x+2 and we know that parallel lines have the same slope.
Therefore, we have the following information:
- m = 5
- b = -3
$latex y=mx+b$
$latex y=5x-3$
The equation of the given line is $latex y=5x-3$.
EXAMPLE 5
If a line is parallel to the line y = –x+10 and intersects the y-axis at (0, 3), find its equation.
Solution
Similar to the previous example, we know that parallel lines have the same slope, so we have:
- m = -1
- b = 3
$latex y=mx+b$
$latex y=-x+3$
The equation of the line is $latex y=-x+3$.
EXAMPLE 6
Determine the equation of a line that has a slope of 1/5 and passes through the origin.
Solution
In this case, we know the slope, but we don’t have the y-intercept given explicitly. However, we have that the line passes through the origin, that is, the point (0, 0), so we have the following:
- m = 1/5
- b = 0
$latex y=mx+b$
$latex y=\frac{1}{5}x+0$
$latex y=\frac{1}{5}x$
The equation of the line is $latex y=\frac{1}{5}x$.
EXAMPLE 7
If a line has a slope of 0.25 and a y-intercept of (0, 0.5), what is its equation?
Solution
We have to use the slope-intercept form formula with the following values:
- m = 0.25
- b = 0.5
$latex y=mx+b$
$latex y=0.25x+0.5$
The equation of the given line is $latex y=0.25x+0.5$.
Slope-intercept form of a line – Practice problems
Apply the formula for the slope-intercept form to find the equations of the lines in these problems. If you have trouble with these problems, you can look at the solved examples above.
See also
Interested in learning more about equations of lines? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
