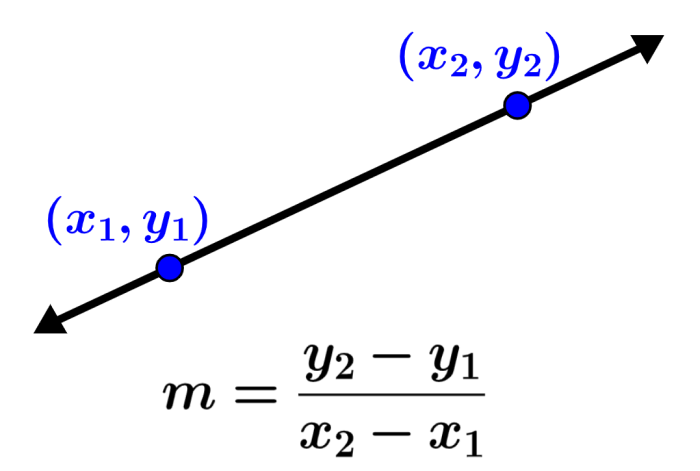
The slope of a line defines the inclination of the line with respect to the x-axis. The slope can be calculated by obtaining the ratio of the difference in the change in y over the change in x. Here, we will learn about the formula that we can use to calculate the slope of a line.
We will learn about the slope of common lines and we will solve some practice problems.
Formula for the slope of a line
The formula for the slope of a line is derived using the coordinates of two points that lie on the line. Therefore, we find the slope of a line by forming a fraction, where the numerator is equal to the difference of the y-coordinates and the denominator is equal to the difference of the x-coordinates. That is, if we have the points $latex A = (x_{1}, y_{1})$ and $latex B = (x_{2}, y_{2})$, the slope formula is:
| Formula for the slope $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ |
Slope of a horizontal line
The slope of a horizontal line can be found by applying the slope formula taking into account that the y-coordinates of all points that lie on a horizontal line are the same. Therefore, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{0}{x_{2}-x_{1}}$
$latex m=0$
This means that the slope of all horizontal lines is equal to 0.
Slope of a vertical line
Vertical lines have no slope since we cannot define the slope of vertical lines numerically. This is because the x-coordinates of all points on a vertical line are the same. Therefore, when we apply the slope formula with vertical lines, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{y_{2}-y_{1}}{0}$
We know that division by 0 is undefined.
Slope of parallel lines
Consider the following two parallel lines, $latex l_{1}$ and $latex l_{2}$, which have slopes α and β. For the lines to be parallel, the slopes must be the same. This means that we have α = β.
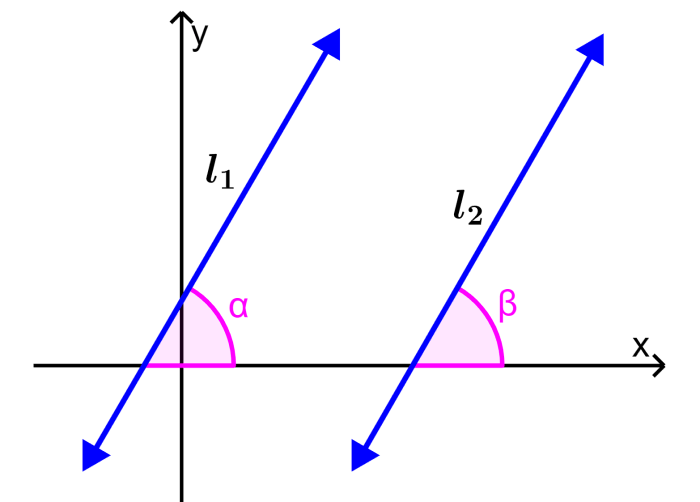
Therefore, two parallel lines always have the same slope. Therefore, if we want to determine if two or more lines are parallel, we have to make sure that their slopes are the same.
Slope of perpendicular lines
In the following diagram, we have the lines $latex l_{1}$ and $latex l_{2}$, which have the slopes α and β:
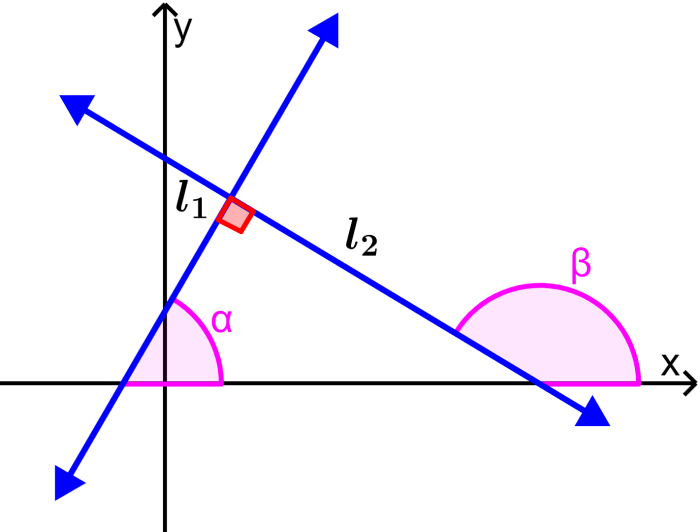
If these lines are perpendicular, we can say that β = α+90°. Also, we can write the slopes as follows:
$latex m_{1}=\tan(\alpha +90^{\circ})$ y $latex m_{2}=\tan(\alpha)$
⇒ $$m_{1}=-\cot(\alpha)=m_{1}=-\frac{1}{\tan(\alpha)}=-\frac{1}{m_{2}}$$
⇒ $latex m_{1}=-\frac{1}{m_{2}}$
⇒ $latex m_{1}\times {m_{2}}=-1$
Therefore, for two lines to be perpendicular, the product of their slopes must equal -1. Alternatively, we can think of two perpendicular lines as having slopes that are the negative reciprocal of each other.
Slope of a line – Examples with answers
EXAMPLE 1
The points (1, 1) and (3, 5) are part of a line. What is the slope of the line?
Solution
The points given are:
- $latex (x_{1}, y_{1})=(1, 1)$
- $latex (x_{2}, y_{2})=(3, 5)$
Using the coordinates of the points given in the slope formula, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{5-1}{3-1}$
$latex m=\frac{4}{2}$
$latex m=2$
The slope of the line is 2.
EXAMPLE 2
What is the slope of a line that has the points (2, 1) and (4, 5)?
Solution
We have the following coordinates:
- $latex (x_{1}, y_{1})=(2, 1)$
- $latex (x_{2}, y_{2})=(4, 5)$
We use the slope formula with the given coordinates:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{5-1}{4-2}$
$latex m=\frac{4}{2}$
$latex m=2$
The slope of the line is 2.
EXAMPLE 3
A line contains the points (2, 3) and (6, 5). What is its slope?
Solution
We have the following points:
- $latex (x_{1}, y_{1})=(2, 3)$
- $latex (x_{2}, y_{2})=(6, 5)$
Applying the slope formula with these points, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{5-3}{6-2}$
$latex m=\frac{2}{4}$
$latex m=\frac{1}{2}$
The slope of the line is $latex \frac{1}{2}$.
EXAMPLE 4
We have the points (3, 2) and (6, 3) that are part of a line. What is the slope?
Solution
We have the following values:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(6, 3)$
Using the slope formula with these values, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{3-2}{6-3}$
$latex m=\frac{1}{3}$
The slope of the line is $latex \frac{1}{3}$.
EXAMPLE 5
The points (-3, 2) and (3, 4) are part of a line. What is its slope?
Solution
We have the following coordinates:
- $latex (x_{1}, y_{1})=(-3, 2)$
- $latex (x_{2}, y_{2})=(3, 4)$
Applying the slope formula with these coordinates, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{4-2}{3-(-3)}$
$latex m=\frac{2}{6}$
$latex m=\frac{1}{3}$
The slope of the line is $latex \frac{1}{3}$.
EXAMPLE 6
Determine the slope of a line containing the points (-1, 3) and (6, -4).
Solution
We write the values as follows:
- $latex (x_{1}, y_{1})=(-1, 3)$
- $latex (x_{2}, y_{2})=(6, -4)$
Using these values in the formula, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-4-3}{6-(-1)}$
$latex m=\frac{-7}{7}$
$latex m=-1$
The slope of the line is $latex -1$.
EXAMPLE 7
Determine the slope of a line that contains the points (-3, -2) and (2, -7).
Solution
We have the points:
- $latex (x_{1}, y_{1})=(-3, -2)$
- $latex (x_{2}, y_{2})=(2, -7)$
Now, we use these coordinates in the slope formula:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-7-(-2)}{2-(-3)}$
$latex m=\frac{-5}{5}$
$latex m=-1$
The slope of the line is -1.
EXAMPLE 8
If a line has the points (-2, 1) and (6, -3), what is its slope?
Solution
We have the coordinates:
- $latex (x_{1}, y_{1})=(-2, 1)$
- $latex (x_{2}, y_{2})=(6, -3)$
We apply the slope formula with the given coordinates:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-3-1}{6-(-2)}$
$latex m=\frac{-4}{8}$
$latex m=-\frac{1}{2}$
The slope of the line is $latex -\frac{1}{2}$.
Slope of a line – Practice problems
What is the slope of a line that contains the points (-3,-2) and (1, -10)?
Write the answer in the input box.
See also
Interested in learning more about distance, midpoint, and slope on the plane? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
