The distance from a point to a line is the shortest distance that can join the straight line with that point. The shortest distance will always be a perpendicular segment to the line. We can derive a formula for the distance of a point from a line using trigonometry and the equation of a line.
In this article, we will learn about the formula that we can use to calculate the distance from a point to a line. Also, we will use this formula to solve some practice problems.
What is the distance of a point from a line?
The distance of a point from a line is the shortest distance that can join them. That is, it is the smallest possible length that we need to move from the point to a point on the line. This distance will always be perpendicular to the given line.
For example, let’s consider the following line L and a point p that is not part of the line:
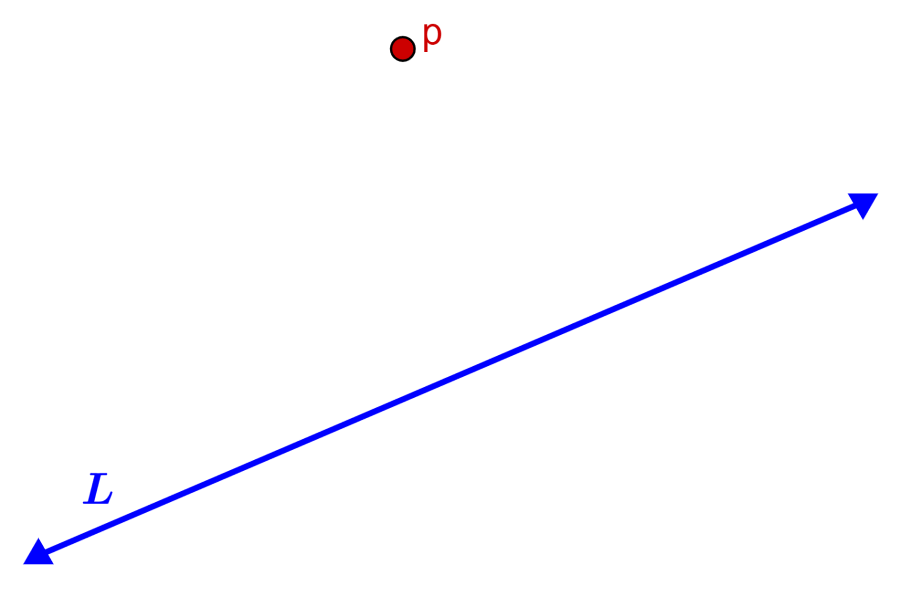
To measure the distance from the line to point p, we can use the equation of a line and the distance formula. In addition, we also consider a right triangle XYZ, which has a right angle at Y:
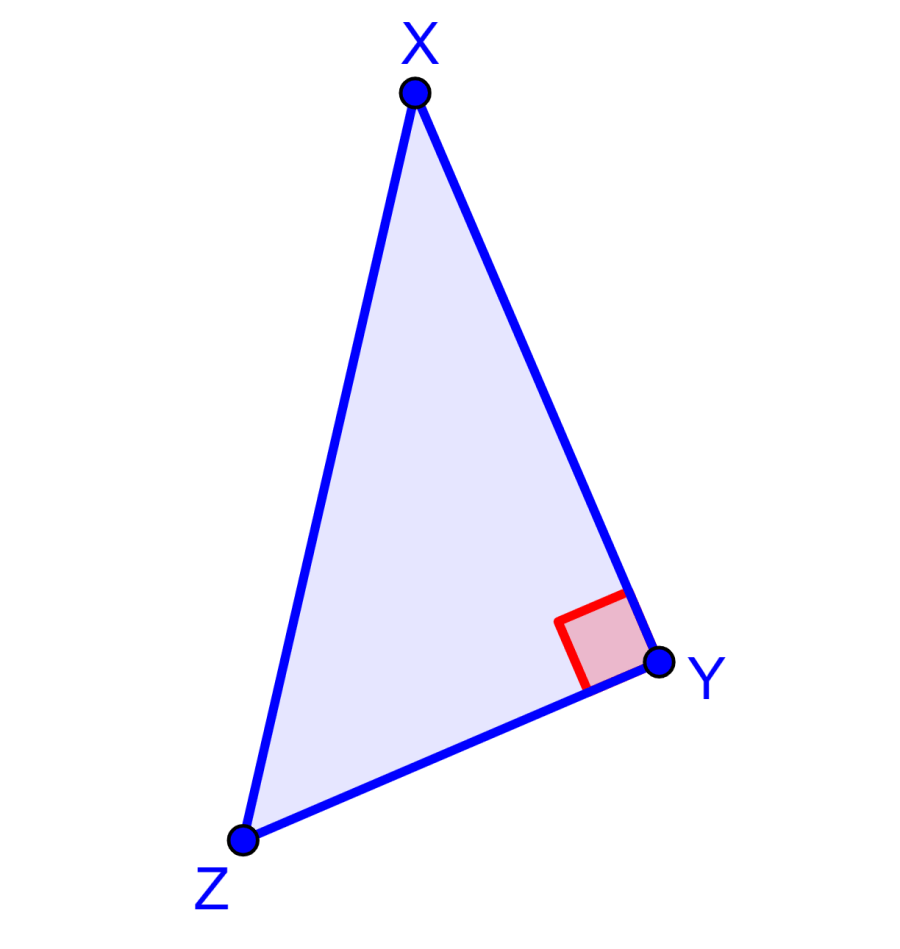
In this triangle, angle Y is equal to 90° and segment XZ is the hypotenuse. The hypotenuse XZ will always be longer than the perpendicular segment from X to YZ. Therefore, we can use this in the following diagram:
Segment XY is perpendicular to line L. On the other hand, Z can be any point on line R. We can see that XY will always be shorter than XZ no matter where Z is located on the line.
This means that the shortest distance of a point from a line will always be a perpendicular segment from the line to the point.
Proof of the formula for the distance of a point from a line
The perpendicular distance of a point $latex P(x_{1},~y_{1})$ from a line $latex ax+by+c=0$ can be found using the following formula:
| $$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$ |
We can derive this formula using the following diagram:
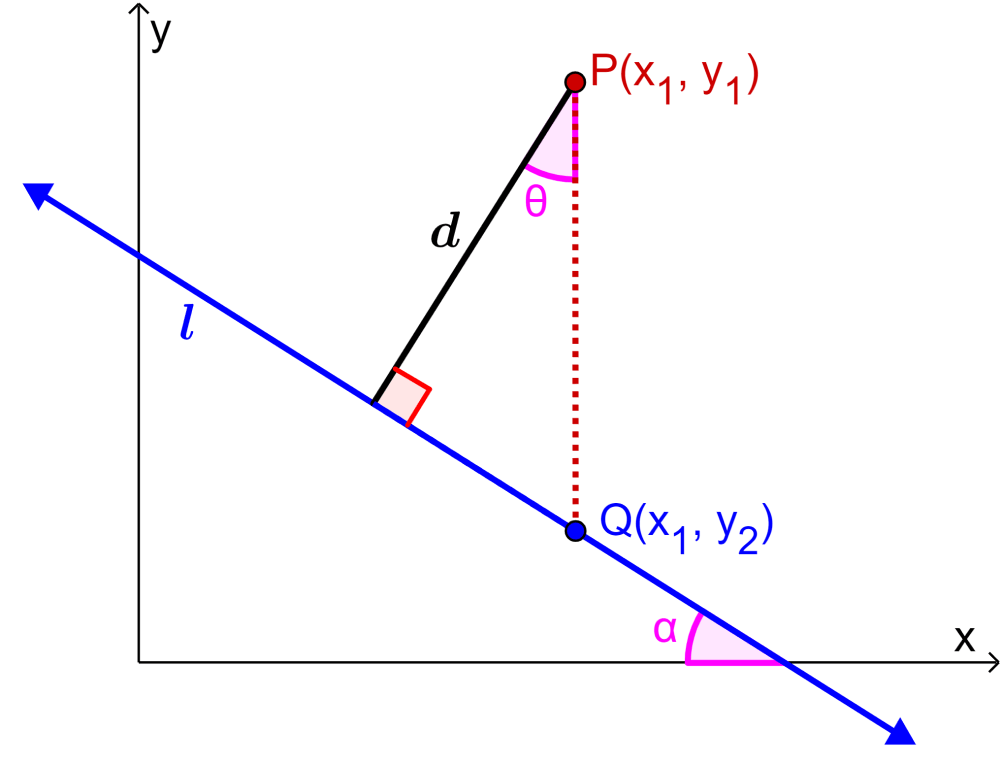
The point $latex Q(x_{1},~y_{2})$ lies on the line $latex ax+by+c=0$ and is directly below P.
Using point Q in the equation of the line, we have $latex ax_{1}+by_{2}+c=0$. If we solve for $latex y_{2}$, we have:
$$y_{2}=-\left(\frac{ax_{1}+c}{b}\right)$$
Since points P and Q are at the same x-coordinate, we have: $latex PQ=y_{1}-y_{2}$. Using this in the equation obtained above, we have:
$$PQ=y_{1}+\frac{ax_{1}+c}{b}$$
$$=\frac{ax_{1}+by_{1}+c}{b}$$
Now, looking at the diagram, we can deduce that d is equal to the cosine of θ multiplied by PQ: $latex d=PQ\cos(\theta)$. Therefore, we have:
$$d=\frac{ax_{1}+by_{1}+c}{b}\cos(\theta)~~[1]$$
It only remains for us to find an expression for cos(θ) to complete the proof of the formula.
Using the diagram again in conjunction with angle theorems, we can deduce that angle θ is equal to angle α. Also, since we can write the equation of line l as $latex y=-\frac{a}{b}x-c$, the slope of l is $latex-\frac{a}{b}$.
This means that $latex \tan(\theta)=\tan(\alpha)=\frac{a}{b}$. Remembering that the tangent is equal to the opposite side over the adjacent side, we can obtain the following diagram, where we use the Pythagorean theorem to obtain the hypotenuse:
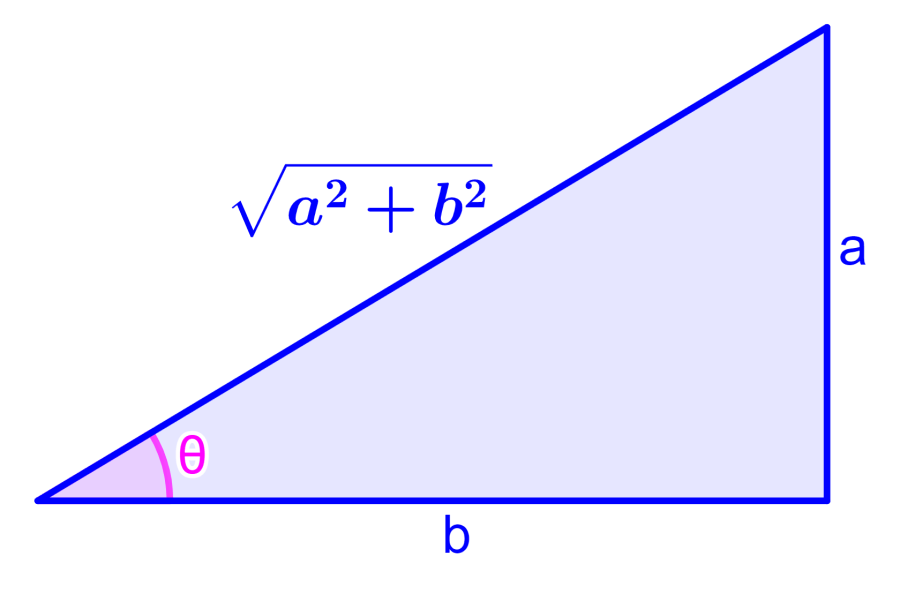
Therefore, we have
$$\cos(\theta)=\frac{b}{\sqrt{a^2+b^2}}~~[2]$$
Substituting equation [2] into equation [1], we have:
$$d=\left(\frac{ax_{1}+by_{1}+c}{b}\right)\frac{b}{\sqrt{a^2+b^2}}$$
$$d=\left(\frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right)$$
Note: The absolute value sign is given to the result since in this proof we assume that the line has a negative slope and that point P is above the line. If point P was below the line, we would have introduced a negative sign in the formula.
Distance of a point from a line – Examples with answers
The following examples are solved using the formula for the distance of a point from a line. Each example has its respective solution, but try to solve the problems yourself.
EXAMPLE 1
Find the distance of the point (2, 3) from the line $latex x+y+2=0$.
Solution
We have to use the distance formula with the following values:
- x1 = 2
- y1 = 3
- a = 1
- b = 1
- c = 2
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(1)(2)+(1)(3)+2}{\sqrt{1^2+1^2}}\right|$$
$$=\left| \frac{2+3+2}{\sqrt{1+1}}\right|$$
$$=\left| \frac{7}{\sqrt{2}}\right|=\frac{7\sqrt{2}}{2}$$
$latex \approx 4.95$
The distance of the point from the line is 4.95 units.
EXAMPLE 2
Determine the distance of the point (5, 5) from the line $latex 2x-y+3=0$.
Solution
We start by acknowledging the following values:
- x1 = 5
- y1 = 5
- a = 2
- b = -1
- c = 3
Now, we use these values in the distance formula:
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(2)(5)+(-1)(5)+3}{\sqrt{2^2+(-1)^2}}\right|$$
$$=\left| \frac{10-5+3}{\sqrt{4+1}}\right|$$
$$=\left| \frac{8}{\sqrt{5}}\right|=\frac{8\sqrt{5}}{5}$$
$latex \approx 3.578$
The distance of the point from the line is 3.578 units.
EXAMPLE 3
What is the distance of the point (-2, 5) from the line $latex -2x+3y+4=0$?
Solution
The values given are as follows:
- x1 = -2
- y1 = 5
- a = -2
- b = 3
- c = 4
Applying the distance formula with these values, we have:
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-2)(-2)+(3)(5)+4}{\sqrt{(-2)^2+3^2}}\right|$$
$$=\left| \frac{4+8+4}{\sqrt{4+9}}\right|$$
$$=\left| \frac{16}{\sqrt{13}}\right|=\frac{16\sqrt{13}}{13}$$
$latex \approx 4.438$
The distance of the point from the line is 4.438 units.
EXAMPLE 4
Determine the distance of the point (3, -2) from the line $latex -3x-2y-4=0$
Solution
We apply the distance formula seen above with the following values:
- x1 = 3
- y1 = -2
- a = -3
- b = -2
- c = -4
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-3)(3)+(-2)(-2)-4}{\sqrt{(-3)^2+(-2)^2}}\right|$$
$$=\left| \frac{-9+4-4}{\sqrt{9+4}}\right|$$
$$=\left| \frac{-9}{\sqrt{13}}\right|=\frac{9\sqrt{13}}{13}$$
$latex \approx 2.496$
The distance of the point from the line is 2.496 units.
EXAMPLE 5
Find the distance of the point (-2, 4) from the line $latex -2x+5y-2=0$
Solution
We have to use the formula we learned using the following values:
- x1 = -2
- y1 = 4
- a = -2
- b = 5
- c = -2
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-2)(-2)+(5)(4)-2}{\sqrt{(-2)^2+5^2}}\right|$$
$$=\left| \frac{4+20-2}{\sqrt{4+25}}\right|$$
$$=\left| \frac{22}{\sqrt{29}}\right|=\frac{22\sqrt{29}}{29}$$
$latex \approx 4.085$
The distance of the point from the line is 4.085 units.
EXAMPLE 6
What is the distance of the point (0, 3) from the line $latex -5x+2y+10=0$?
Solution
We have to use the distance formula with the following values:
- x1 = 0
- y1 = 3
- a = -5
- b = 2
- c = 10
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-5)(0)+(2)(3)+10}{\sqrt{(-5)^2+2^2}}\right|$$
$$=\left| \frac{0+6+10}{\sqrt{25+4}}\right|$$
$$=\left| \frac{16}{\sqrt{29}}\right|=\frac{16\sqrt{29}}{29}$$
$latex \approx 2.971$
The distance of the point from the line is 2.971 units.
EXAMPLE 7
Determine the distance of the point (-4, 4) from the line $latex 3x+10y-5=0$.
Solution
We are going to use the formula for the perpendicular distance of a point from a line with the following values:
- x1 = -4
- y1 = 4
- a = 3
- b = 10
- c = -5
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(3)(-4)+(10)(4)-5}{\sqrt{3^2+10^2}}\right|$$
$$=\left| \frac{-12+40-5}{\sqrt{9+100}}\right|$$
$$=\left| \frac{23}{\sqrt{109}}\right|=\frac{23\sqrt{109}}{109}$$
$latex \approx 2.203$
The distance of the point from the line is 2.203 units.
Distance of a point from a line – Practice problems
Try to solve the following problems by applying the formula for the distance of a point from a line. Click “Check” to verify that the selected answer is correct.
See also
Interested in learning more about equations of lines? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
