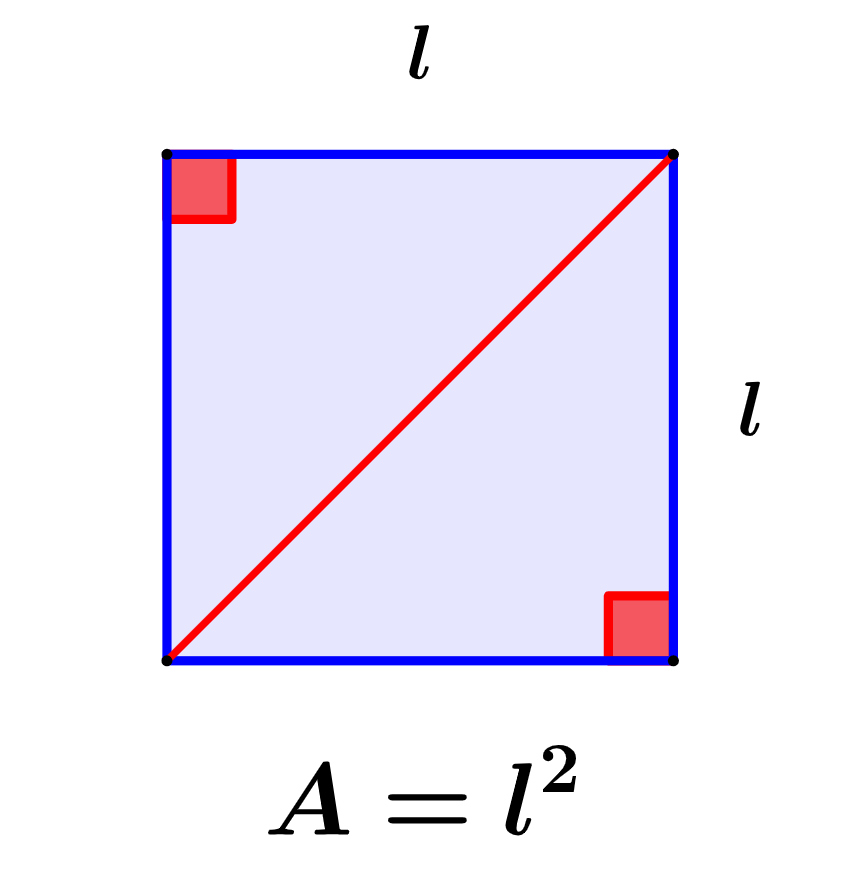
The area of a square is defined as the number of square units it takes to fill a square. In general, the area is defined as the occupied region within the limits of a two-dimensional figure. The measurement is made in square units, where the standard unit is square meters (m²). To calculate the area of a figure, there are predefined formulas that we can use.
Here, we will learn about the area of a square, we will learn about its formula and we will use it to solve some problems.
How to find the area of a square?
The area is the space covered by the object, that is, it is the region occupied by any figure. When we measure the area of a square, we only consider the length of one of its sides since all its sides are equal. To calculate the area of a square, we simply square the length of one of its sides:
$latex A={{l}^2}$
where,
- A represents the area of the square
- l represents the length of one of the sides of the square
Let’s look at why this formula is true by plotting a square. We want to find the area of a square that has sides of length 5 cm. Using this dimension, we draw a square on paper that has a 1 cm × 1 cm grid. The square we draw covers 25 of these small squares.
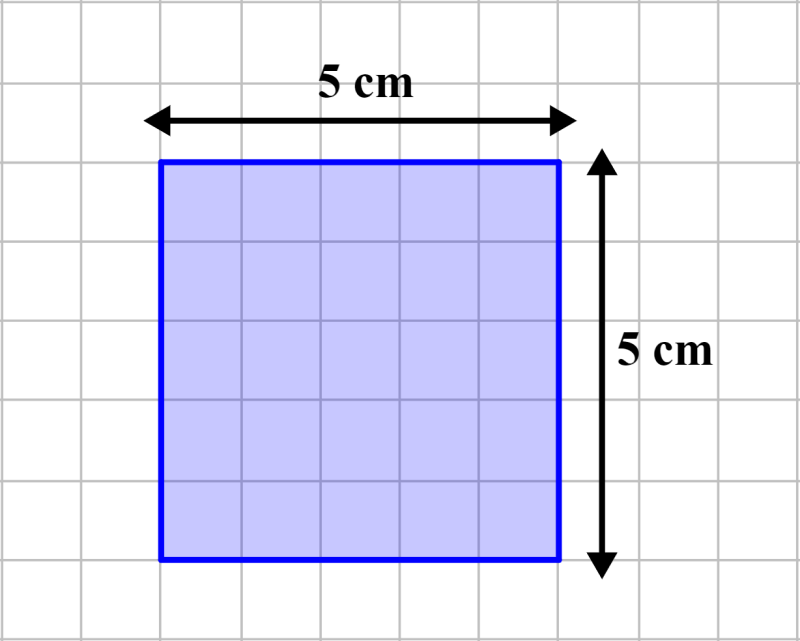
Therefore, the area of the square is 25 cm², which can be written as 5 cm × 5 cm, that is, we have side × side. Thus, we have that the area of the square is:
| Area = Side × SideArea = Side² $latex A={{l}^2}$ |
The following are some unit conversions that might be helpful:
- 1 m = 100 cm
- 1 m² = 10 000 cm²
- 1 km = 1000 m
- 1 km² = 1 000 000 m²
Area of a square – Examples with answers
The following examples are solved using the formula for the area of a square detailed above. Try to solve the exercises yourself before looking at the solution.
EXAMPLE 1
Find the area of a square that has sides of length 12 m.
Solution
We have that the length of one side of the square is 12 m.
We can use the formula $latex A = {{l}^2}$ with the given value:
$latex A={{l}^2}$
$latex A={{12}^2}$
$latex A=144$
Thus, the area of the square is 144 m².
EXAMPLE 2
What is the area of a square that has sides of length 15 cm?
Solution
In this case, the length of one side of the square is 15 cm.
We have the formula $latex A={{l}^2}$, so we substitute l with the given value:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
Therefore, the area of the square is 225 cm².
EXAMPLE 3
A square wall has sides that are 6 m long. What is the cost of painting the wall at a rate of USD 0.5 per square meter?
Solution
We have to calculate the area of the wall to know how many square meters we have to paint.
Therefore, we use the formula $latex A={{l}^2}$ with a length of 6 m:
$latex A={{l}^2}$
$latex A={{6}^2}$
$latex A=36$
The area of the wall is 36 square meters. If the rate is USD 0.5 per square meter, the cost will be:
$latex 36\times 0.5=18$ dollars
EXAMPLE 4
What is the length of the sides of a square that has an area of 121 cm²?
Solution
In this case, we have to calculate the length of the sides starting from the area. We use the area formula and take the square root of both sides to get the length of one side:
$latex A={{l}^2}$
$latex 121={{l}^2}$
$latex l=\sqrt{121}$
$latex l=11$
Therefore, the length of one side of the square is 11 cm.
EXAMPLE 5
A square floor that has sides of length 40 m is to be covered with ceramic. If each tile has sides that are 2m long, how many tiles are needed to cover the floor?
Solution
We have to find both the area of the floor and the area of each ceramic. Therefore, the area of the floor is:
$latex A_{f}={{l_{f}}^2}$
$latex A_{f}={{40}^2}$
$latex A_{f}=1600$
The area of the floor is 1600 m² and the area of each ceramic is:
$latex A_{c}={{l_{c}}^2}$
$latex A_{c}={{2}^2}$
$latex A_{c}=4$
The area of each ceramic is 4 m². Thus, we need:
$latex \frac{A_{f}}{A_{c}}=\frac{1600}{4}=400$ ceramics
Area of a square – Practice problems
Put into practice what you have learned about the area of a square to solve the following problems. Select an answer and click “Check” to verify that you chose the correct one. Check out the solved examples above in case you need help.
See also
Interested in learning more about squares? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
