A square is a two-dimensional figure with four equal sides, in which its four angles measure 90 degrees. The properties of squares are quite similar to those of a rectangle, but the difference between the two is that, a rectangle only has opposite sides that are equal. The other properties of the square, such as area and perimeter, also differ from those of the rectangle.
Here, we will look at the fundamental properties of squares. In addition, we will look at some examples of these properties.
Fundamental properties of squares
The following are the fundamental properties of squares:
- The four interior angles of a square are equal to 90°.
- All four sides of a square are congruent (the length is the same).
- The opposite sides of the square are parallel to each other.
- The diagonals bisect each other by 90°, that is, they are perpendicular.
- The two diagonals are equal (they are the same length).
- The square has four vertices and four sides.
- The square diagonal divides it into two similar isosceles triangles.
- The length of the diagonals is greater than the length of the sides of the square.
- The diagonals of the square are diameters of the circuncircle of the square.
- A square is an equilateral with four equal sides and four equal interior angles.
- A square is a rhombus with four equal angles (each angle has 90°).
- A square is a rectangle, in which its two adjacent sides are equal.
- A square is a parallelogram with the four interior angles equal to 90° and the adjacent sides equal in length.
Formulas for squares
The following are some important formulas related to squares:
Area of a square: A=l², where l is the length of each side of the square:
| Area of square = (side)²=l² |
Perimeter of square: p=total length of all sides of the square = 4l, where l is the length of each side of the square:
| Perimeter = 4 × side=4l |
Diagonal of a square: Each of the diagonals divides the square into two equal right triangles, where the diagonal is the hypotenuse of the triangles.
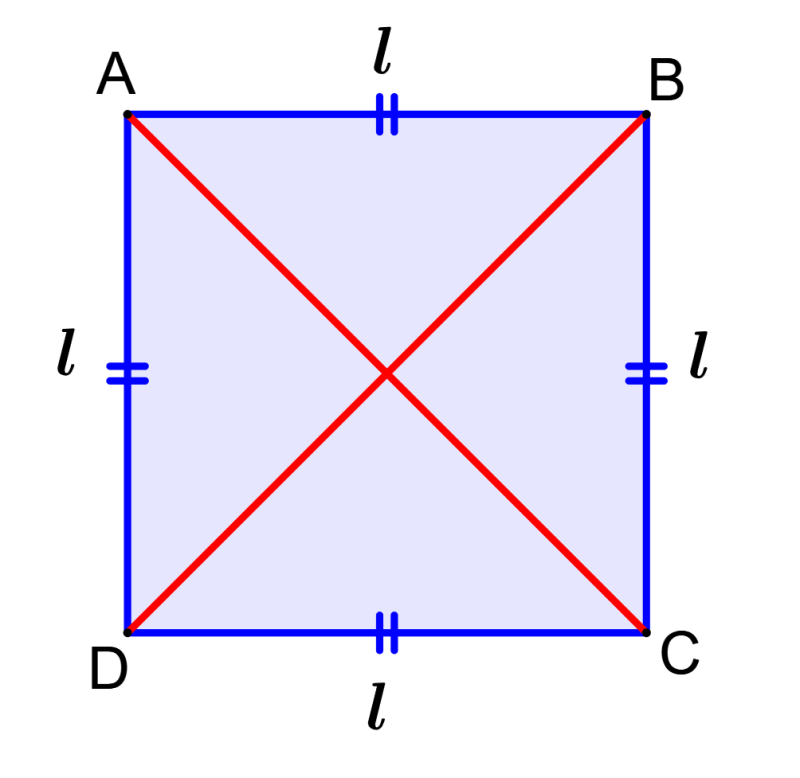
We can apply the Pythagorean theorem to find the length of the hypotenuse:
$latex {{d}^2}={{side}^2}+{{side}^2}$
We know that a square has all its sides with the same length, so we have:
$latex {{d}^2}=2{{side}^2}$
$latex d=\sqrt{2}~l$
Therefore,
| Diagonal =$latex \sqrt{2}~side=\sqrt{2}~l$ |
Square problems examples
The following are some examples of solved square problems.
EXAMPLE 1
What is the perimeter of a square that has sides with a length of 13 m?
Solution: We know that the formula for the perimeter of a square is 4l, where l is the length of the sides of the square. Thus, using $latex l=13$, we have:
$latex p=4l$
$latex p=4(13)$
$latex p=52$
The perimeter of the square is 52 m.
EXAMPLE 2
If a square has sides that are 15 cm long, what is its area?
Solution: A square has all equal sides and its area can be calculated by squaring one of its sides. Therefore, using the given length, we have:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
The area of the square is 225 cm².
EXAMPLE 3
What is the length of the diagonal of a square that has sides with a length of 8 m?
Solution: The diagonal of the square is calculated using the Pythagorean theorem. Then, to simplify, we obtain the following formula, in which we use $latex l=8$:
$latex d=\sqrt{2}~l$
$latex d=\sqrt{2}~(8)$
$latex d=8\sqrt{2}$
The diagonal of the square has a length of $latex 8 \sqrt{2}$ m.
See also
Interested in learning more about squares? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
