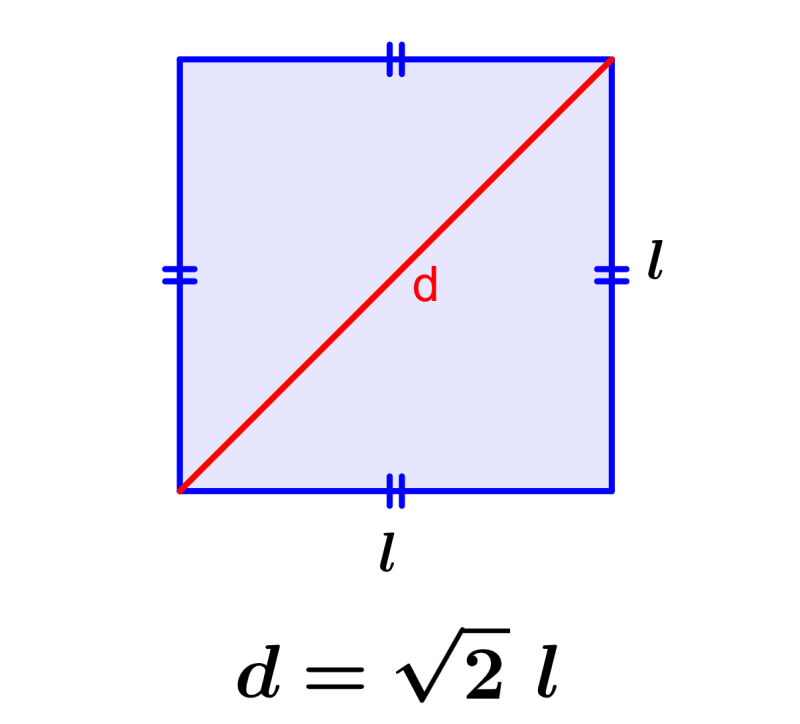
In geometry, a square is a regular quadrilateral, which has four sides of equal length and four angles that measure 90 degrees. A square can have two diagonals. Each of the diagonals can be formed by joining the vertices of the square that are diagonally opposite. The length of the diagonal of a square can be calculated using the Pythagorean theorem. The Pythagorean theorem is simplified by recognizing that the required side lengths are equal.
Here, we will learn about the formula that can be used to calculate the length of the diagonal of a square. In addition, we will look at some examples in which we will use this formula.
How to find the diagonal of a square?
We can calculate the diagonal of a square using a formula derived from the Pythagorean theorem. Consider a square ABCD that has sides with a length of “l” cm.
We see that the lines AD and BC are the diagonals of the square:
We can clearly see that a diagonal divides the square into two equal triangles $latex \Delta ACD$ and $latex \Delta BDC$. We are going to use one of the triangles to calculate the length of the diagonal.
We can apply the Pythagorean theorem in $latex \Delta ACD$ to get the length of the diagonal. Therefore, we have:
$latex {{AC}^2}={{AD}^2}+{{CD}^2}$
We know that $latex AD=CD=l$. Thus, we can plug this into the equation above:
$latex {{AC}^2}={{l}^2}+{{l}^2}$
$latex {{AC}^2}=2{{l}^2}$
$latex AC=\sqrt{2}~l$
Therefore, the length of the diagonal of a square is:
| $latex d=\sqrt{2}~l$ |
The properties of the diagonals of the squares are as follows:
• Both diagonals are congruent (they have the same length).
• Both diagonals bisect each other, that is, the point where the diagonals intersect is the midpoint.
• A diagonal divides the square into two isosceles right triangles.
Diagonal of a square – Examples with answers
The following examples are solved using the diagonal formula indicated above. Try to solve the examples yourself before looking at the solution.
EXAMPLE 1
A square has sides with a length of 12 m. What is the length of its diagonal?
Solution
We have that the length of the sides of the square is 12 m. Therefore, we can find its diagonal as follows:
$latex d=\sqrt{{{side}^2}+{{side}^2}}$
$latex d=\sqrt{2{{side}^2}}$
$latex d=side\sqrt{2}$
$latex d=12\sqrt{2}$
Thus, the diagonal has a length of $latex 12 \sqrt{2}$ m.
EXAMPLE 2
What is the length of the diagonal of a square that has sides with a length of 17 cm?
Solution
The length of the sides of the square is 17 cm. Therefore, its diagonal can be calculated as follows:
$latex d=\sqrt{{{side}^2}+{{side}^2}}$
$latex d=\sqrt{2{{side}^2}}$
$latex d=side\sqrt{2}$
$latex d=17\sqrt{2}$
Therefore, the diagonal of the square has a length of $latex 17\sqrt{2}$ cm.
EXAMPLE 3
Find the length of the diagonal of a square that has sides of length 25 cm.
Solution
The diagonal of a square is calculated using the Pythagorean theorem with the lengths of its sides. In this case, the sides of the square are 25 cm long:
$latex d=\sqrt{{{side}^2}+{{side}^2}}$
$latex d=\sqrt{2{{side}^2}}$
$latex d=side\sqrt{2}$
$latex d=25\sqrt{2}$
Thus, the diagonal of the square measures $latex 25\sqrt{2}$ cm.
EXAMPLE 4
We have that the diagonal of a square measures $latex 31 \sqrt{2}$ m. What is the length of its sides?
Solution
In this case, we start from the diagonal and we want to find the length of the sides. Therefore, we use the diagonal formula and solve for the side:
$latex d=side\sqrt{2}$
$latex 31\sqrt{2}=side\sqrt{2}$
$latex side=31$
Therefore, the length of the sides of the square is 31 m.
EXAMPLE 5
The diagonal of a square is $latex 19 \sqrt{2}$ cm. What is the length of its sides?
Solution
We use the diagonal formula, plug in the value of the diagonal and solve for the side:
$latex d=side\sqrt{2}$
$latex 19\sqrt{2}=side\sqrt{2}$
$latex side=19$
Thus, the length of the sides of the square is 19 cm.
Diagonal of a square – Practice problems
The following problems can be used to practice using the formula for the diagonal of a square. Solve the problems and select your answer. Click “Check” to verify that you selected the correct answer.
See also
Interested in learning more about squares? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
