The volume of revolution formed when we rotate an area by 2π around the y-axis can be found by using a definite integral of the square of the equation of the curve and multiplying the result by π. The formula for this volume can be derived using limits and integrals.
In this article, we will learn how to calculate the volume of revolution with respect to the y-axis. We will learn how to derive its formula and apply it in some examples.
CALCULUS
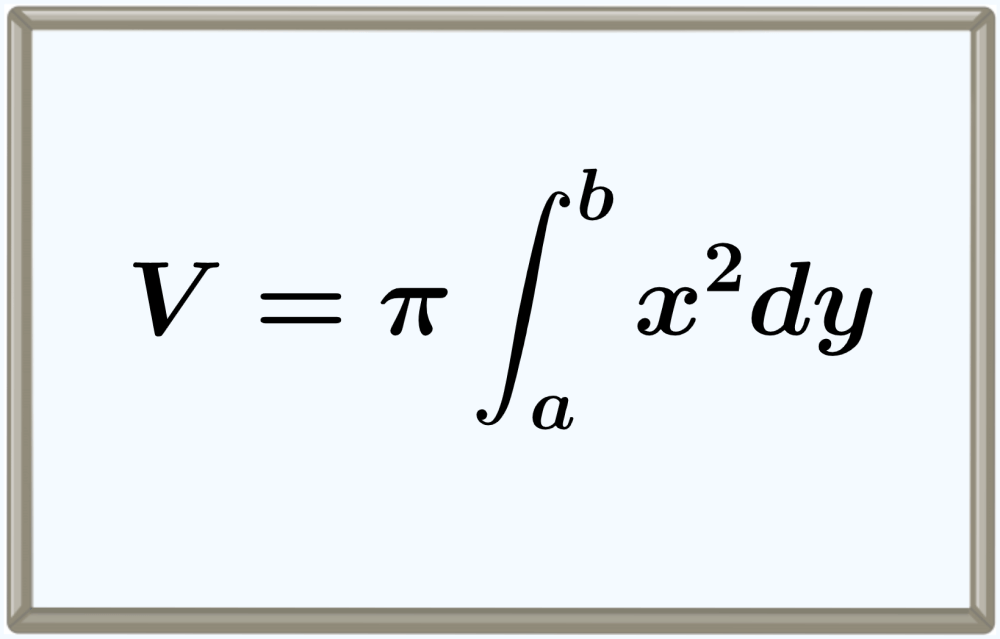
Relevant for…
Learning to calculate the volume of revolution about the y-axis.
CALCULUS
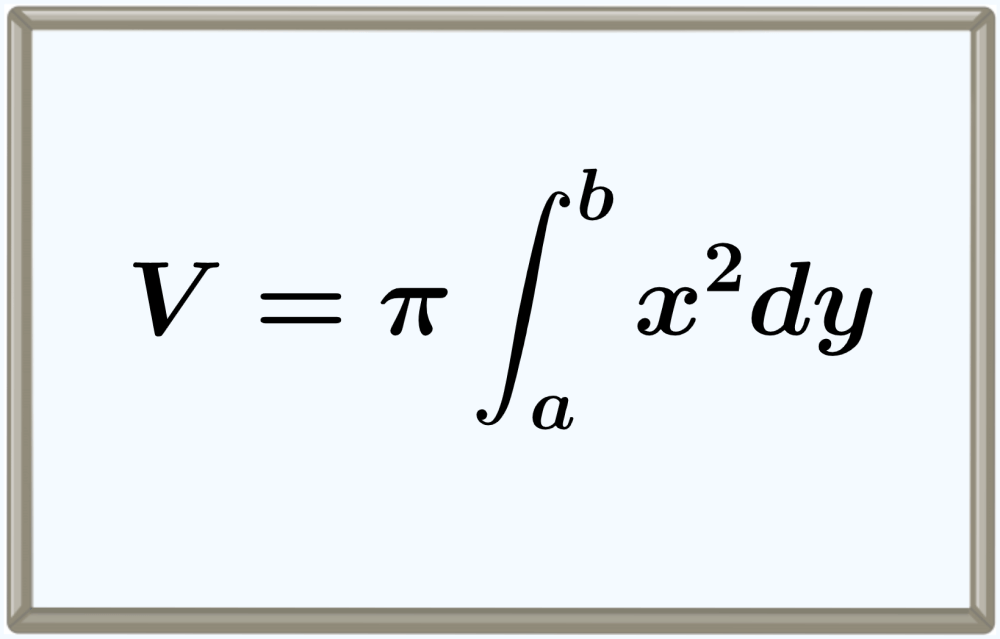
Relevant for…
Learning to calculate the volume of revolution about the y-axis.
How to find the volume of revolution around the y-axis
The volume of a solid of revolution formed by rotating an area by 2π radians around the y-axis can be found in the same way as when it is with respect to the x-axis. Then, we have the following formula
$$V=\pi \int_{a}^{b} x^2 d y$$
In this case, we must take into account that $latex dy$ indicates that the limits $latex a$ and $latex b$ are limits of $latex y$.
Then, we follow the following process to apply the formula correctly:
1. Find an expression for x in terms of y.
For example, if $latex y=x^2$, then $latex x=\sqrt{y}$.
2. Square the expression obtained in step 1.
That is, we have $latex x^2$.
3. Evaluate the definite integral $latex \int_{a}^{b} x^2 d y$.
For this, we substitute the expression for $latex x^2$ from step 2.
4. Multiply by π the result of step 3 to find the volume of the solid formed.
You can make a revision of definite integrals in this article: How to find definite integrals.
Volume of revolution around the y-axis – Examples with answers
EXAMPLE 1
Find the volume generated when $latex y=\frac{1}{2}x$ is rotated about the y-axis, from $latex y=0$ to $latex y=6$.
Solution
We begin by recalling the formula for the volume of revolution around the y-axis:
$$V=\pi \int_{a}^{b} x^2 d y$$
Now, we have to find an expression for $latex x $ in terms of y. We can accomplish this by solving for x:
$latex y=\frac{1}{2}x$
$latex x=2y$
We substitute this equation into the volume formula and solve the definite integral:
$$V=\pi \int_{0}^{6} (2y)^2 d y$$
$$=\pi \int_{0}^{6} 4y^2 d y$$
$$=\pi \left[ \frac{4y^3}{3} \right]_{0}^{6}$$
$$=\pi \left( \frac{864}{3} \right)-(0)$$
$latex V=288\pi $
EXAMPLE 2
What is the volume generated when $latex y=x^2$ is rotated around the y-axis, from $latex y=0$ to $latex y=9$?
Solution
The formula for the volume of a solid obtained by rotating to a curve around the y-axis is:
$$V=\pi \int_{a}^{b} x^2 d y$$
We need an expression for $latex x $ in terms of y, so we find it as follows:
$latex y=x^2$
$latex x=\sqrt{y}$
Using the volume formula with the expression found and solving the definite integral, we have:
$$V=\pi \int_{0}^{9} (\sqrt{y})^2 d y$$
$$=\pi \int_{0}^{9} y d y$$
$$=\pi \left[ \frac{y^2}{2} \right]_{0}^{9}$$
$$=\pi \left( \frac{81}{2} \right)-(0)$$
$$V=\frac{81\pi}{2} $$
EXAMPLE 3
If we have the curve $latex y=x^3$, what is the volume generated by rotating it around the y-axis, from $latex y=1$ to $latex y=8$?
Solution
We have the curve $latex y=x^3$. Then, $latex x^2$ is equal to:
$latex y=x^3$
$latex x^2=y^{\frac{2}{3}}$
Then, when we substitute $latex x^2$ into the volume formula and solve the definite integral, we have:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{1}^{8} y^{\frac{2}{3}} d y$$
$$=\pi \left[ \frac{3y^{\frac{5}{3}}}{5} \right]_{1}^{8}$$
$$=\pi \left[ \frac{3(8)^{\frac{5}{3}}}{5}-\frac{3(1)^{\frac{5}{3}}}{5} \right]$$
$$V=\frac{93\pi}{5} $$
EXAMPLE 4
Find the volume generated when the curve $latex y=\sqrt{x}$ is rotated around the y-axis from $latex y=0$ to $latex y=3$.
Solution
We can find an expression for $latex x$ by squaring both sides of the equation:
$latex y=\sqrt{x}$
$latex x=y^2$
When we use this expression in the volume formula and solve the definite integral, we have:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$V=\pi \int_{0}^{3} y^4 d y$$
$$=\pi \left[ \frac{y^5}{5} \right]_{0}^{3}$$
$$=\pi \left( \frac{243}{5}\right)-(0)$$
$$V=\frac{243\pi}{5} $$
EXAMPLE 5
What is the volume generated when $latex y=x^4$ is rotated around the y-axis, from $latex y=1$ to $latex y=4$?
Solution
In this case, we have the equation $latex y=x^4$, so we can find an expression for $latex x^2$ by taking the square root of both sides:
$latex y=x^4$
$latex x^2=\sqrt{y}$
$latex x^2=y^{\frac{1}{2}}$
Using this expression in the volume formula, we can solve for the definite integral:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{1}^{4} y^{\frac{1}{2}} d y$$
$$=\pi \left[ \frac{2y^{\frac{3}{2}}}{3} \right]_{1}^{4}$$
$$=\pi \left( \frac{16}{3} \right)-\left( \frac{2}{3} \right)$$
$$V= \frac{14\pi}{3} $$
EXAMPLE 6
Find the volume of revolution of $latex y=x-1$ with respect to the x-axis from $latex y=2$ to $latex y=5$.
Solution
We start by finding an expression for x in terms of y. Then, we have:
$latex y=x-1$
$latex x=y+1$
Now, we use that expression in the formula for the volume of revolution and solve the definite integral:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{2}^{5} (y+1)^2 d y$$
$$=\pi \int_{2}^{5} (y^2+2y+1) d y$$
$$=\pi \left[ \frac{y^3}{3}+y^2+y \right]_{2}^{5}$$
$$=\pi \left( \frac{125}{3}+25+5 \right)-\left( \frac{8}{3}+4+2 \right)$$
$$=\pi \left( \frac{215}{3} \right)-\left( \frac{26}{3} \right)$$
$$=\pi \left( \frac{249}{3} \right)$$
$latex V=63\pi $
Volume of revolution around the y-axis – Practice problems
Find the volume of the solid formed by rotating $latex y=\frac{1}{2}x+3$ about the y axis from $latex y=4$ to $latex y=6 $.
Write the answer in the input box.
See also
Interested in learning more about integrals of functions? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
