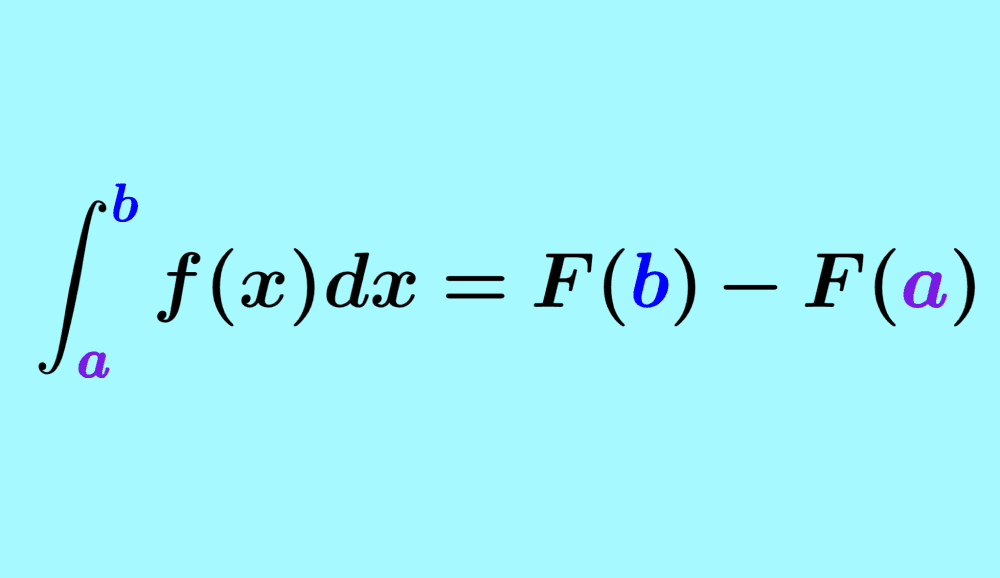Definite integrals are characterized by resulting in a specific or defined value. To find the definite integral of a function, we have to evaluate the integral using the limits of integration. The integral in the lower limit is subtracted from the integral in the upper limit.
Here, we will learn how to solve definite integrals. We will explore 10 examples with answers on definite integrals of functions. Then, we will look at some practice problems to apply everything learned about this type of integral.
Process used to find the definite integral of a function
Suppose we have the integral $latex F=\int f(x) dx$. When we solve this integral, we don’t get a specific value, but we get a function of x.
If we want to get a specific value for $latex F$, we have to evaluate it at specific intervals. Therefore, we have:
$$ F= (\text{Area up to }x=b)-(\text{Area up to }x=a)$$
$latex =F(b)-F(a)$
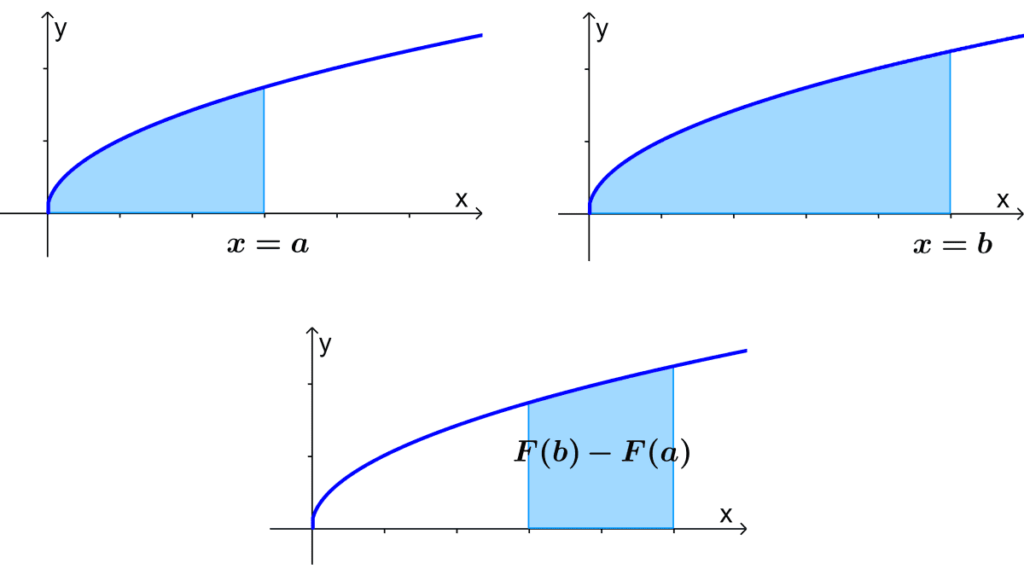
This is written as
$$F= \int_{a}^{b} f(x)dx$$
$latex F= \int_{a}^{b} f(x)dx$ is a definite integral, since it gives us a definitive answer.
- $latex dx$ indicates that the function should be integrated with respect to x.
- The constant $latex a$ is the lower limit of the integral.
- The constant $latex b$ is the upper limit of the integral.
Therefore, if we want to solve the integral $latex \int_{0}^{1} 2xdx$, we follow these steps:
Step 1: Find the integral of the function and use square brackets to enclose the integrated expression and to express the limits of integration. In this case, we have:
$latex \int_{0}^{1} 2xdx=[x^2+c]_{0}^{1}$
Step 2: Evaluate the function at its upper and lower limits. The function in the upper limit is subtracted from the function in the lower limit. Then, we have:
$latex [x^2+c]_{0}^{1}=[(1)^2+c]-[(0)^2+c]$
Step 3: Simplify to a single numeric value:
$latex =[(1)^2+c]-[(0)^2+c]$
$latex =[1+c]-[0+c]$
$latex =1$
We observe that the constants of integration were cancelled. For this reason, it is normal to exclude constants of integration when we are working with definite integrals.
10 Solved examples of definite integrals
EXAMPLE 1
Find the result of the definite integral $latex \int_{0}^{2} 4x^3dx$.
Solution
To solve this definite integral, we have to start by integrating the expression and use square brackets to indicate the limits of integration:
$$\int_{0}^{2} 4x^3dx=[x^4+c]_{0}^{2}$$
Now, we can evaluate the limits. The expression evaluated at the lower limit is subtracted from the expression evaluated at the upper limit:
$$[x^4+c]_{0}^{2}=[(2)^4+c]-[(0)^4+c]$$
When we simplify this, we have:
$latex =[(2)^4+c]-[(0)^4+c]$
$latex =[16+c]-[0+c]$
$latex =16$
We can see that the constant of integration was removed, so we can omit it when we are working with definite integrals.
EXAMPLE 2
Solve the definite integral $latex \int_{2}^{3} (6x^2-1) dx$.
Solution
We start by finding the integral to be evaluated. Keep the limits of integration using square brackets and ignore the constant of integration:
$$\int_{2}^{3} (6x^2-1)dx=[2x^3-x]_{2}^{3}$$
Now that we have the integral, we can evaluate the given limits as follows:
$$[2x^3-x]_{2}^{3}=[2(3)^3-(3)]-[2(2)^3-(2)]$$
Finally, we simplify as follows:
$latex =[2(3)^3-(3)]-[2(2)^3-(2)]$
$latex =[54-3]-[16-2]$
$latex =[51]-[14]$
$latex =37$
EXAMPLE 3
Find the value of the integral $latex \int_{4}^{5} (4x+3)dx$.
Solution
Integrating the given expression and maintaining the limits of integration, we have:
$$\int_{4}^{5} (4x+3)dx=[2x^2+3x]_{4}^{5}$$
Evaluating the limits, we have:
$$[2x^2+3x]_{4}^{5}=[2(5)^2+3(5)]-[2(4)^2+3(4)]$$
Finally, we simplify to obtain:
$latex =[2(5)^2+3(5)]-[2(4)^2+3(4)]$
$latex =[50+15]-[32+12]$
$latex =[65]-[44]$
$latex =21$
EXAMPLE 4
What is the value of the definite integral $latex \int_{2}^{3} (4-3x^2)dx$?
Solution
To find the value of the integral, we have to start by integrating the expression while keeping the limits of integration:
$$\int_{2}^{3} (4-3x^2)dx=[4x-x^3]_{2}^{3}$$
Now, let’s evaluate the limits. Subtract the lower limit from the upper limit:
$$[4x-x^3]_{2}^{3}=[4(3)-(3)^3]-[4(2)-(2)^3]$$
We can simplify to get a single value:
$latex =[4(3)-(3)^3]-[4(2)-(2)^3]$
$latex =[12-27]-[8-8]$
$latex =[-15]-[0]$
$latex =-15$
EXAMPLE 5
Find the result of the definite integral $latex \int_{2}^{8} \frac{1}{x^2} dx$.
Solution
We have to start by finding the integral of the given expression. In this case, we are going to use the laws of exponents to write as follows:
$$\int_{2}^{8} \frac{1}{x^2} dx=\int_{2}^{8} x^{-2} dx$$
$$=[-x^{-1}]_{2}^{8}$$
Now that we have the integral, let’s evaluate the limits:
$$[-x^{-1}]_{2}^{8}=[-(8)^{-1}]-[-(2)^{-1}]$$
Finally, we simplify to obtain a defined value:
$latex =[-(8)^{-1}]-[-(2)^{-1}]$
$$=-\frac{1}{8}+\frac{1}{2}$$
$$=\frac{3}{8}$$
EXAMPLE 6
Find the value of the integral $latex \int_{1}^{2} \frac{4}{x^3} dx$.
Solution
To integrate this expression, we have to use the laws of exponents to write it without the fraction. Then, we have:
$$\int_{1}^{2} \frac{4}{x^3} dx=\int_{1}^{2} 4x^{-3} dx$$
$$=[-2x^{-2}]_{1}^{2}$$
Now, we are going to evaluate the given expression with the given limits of integration:
$$[-2x^{-2}]_{1}^{2}=[-2(2)^{-2}]-[-2(1)^{-2}]$$
When we simplify this, we have:
$latex =[-2(2)^{-2}]-[-2(1)^{-2}]$
$$=-\frac{1}{2}+2$$
$$=\frac{3}{2}$$
EXAMPLE 7
If we have the definite integral $latex \int_{4}^{9} \sqrt{x} dx$, what is its value?
Solution
In this case, we have a square root. Therefore, we write it with a numerical exponent using the laws of exponents:
$$\int_{4}^{9} \sqrt{x} dx=\int_{4}^{9} x^{\frac{1}{2}} dx$$
$$=\left[\frac{2}{3} x^{\frac{2}{3}}\right]_{4}^{9}$$
Now, we evaluate the expression using the limits of integration:
$$=\left[\frac{2}{3} (9)^{\frac{3}{2}}\right]-\left[\frac{2}{3} (4)^{\frac{3}{2}}\right]$$
We can simplify by considering that the exponent $latex \frac{3}{2}$ is equivalent to taking the square root and cubing the result.
$$=\left[\frac{2}{3} (9)^{\frac{3}{2}}\right]-\left[\frac{2}{3} (4)^{\frac{3}{2}}\right]$$
$$=\left[\frac{2}{3} (27)\right]-\left[\frac{2}{3} (8)\right]$$
$$=18-\frac{16}{3}$$
$$=\frac{38}{3}=12~\frac{2}{3}$$
EXAMPLE 8
Find the result of the definite integral $latex \int_{1}^{4} \left( 3- \frac{1}{\sqrt{x}}\right) dx$.
Solution
We start by writing the expression with a numerical exponent to find its integral:
$$\int_{1}^{4} \left( 3- \frac{1}{\sqrt{x}}\right)dx=\int_{1}^{4} ( 3- x^{-\frac{1}{2}})dx$$
$$=\left[ 3x-2 x^{\frac{1}{2}}\right]_{0}^{2}$$
Evaluating the expression using the limits of integration, we have:
$$=\left[ 3(4)-2 (4)^{\frac{1}{2}}\right]-\left[ 3(1)-2 (1)^{\frac{1}{2}}\right]$$
Finally, we can simplify considering that the exponent $latex \frac{1}{2}$ is equivalent to the square root:
$$=\left[ 3(4)-2 (4)^{\frac{1}{2}}\right]-\left[ 3(1)-2 (1)^{\frac{1}{2}}\right]$$
$$=[ 12-4]-\left[ 3-2\right]$$
$latex =8-1$
$latex =7$
EXAMPLE 9
What is the value of the integral $latex \int_{\frac{1}{2}}^{1} 1+\frac{1}{x^2} dx$?
Solution
We rewrite the exponents using the laws of exponents and find the integral of the expression:
$$\int_{\frac{1}{2}}^{1} 1+\frac{1}{x^2} dx=\int_{\frac{1}{2}}^{1} 1+x^{-2} dx$$
$$=\left[x-x^{-1} \right]_{\frac{1}{2}}^{1}$$
Now, we evaluate the expression obtained using the limits of integration:
$$=\left[1-(1)^{-1} \right]-\left[\frac{1}{2}-(\frac{1}{2})^{-1} \right]$$
By simplifying, we can obtain a single value:
$$=\left[1-1 \right]-\left[\frac{1}{2}-2 \right]$$
$$=-\left[\frac{1}{2}-2 \right]$$
$$=\frac{3}{2}$$
EXAMPLE 10
Solve the definite integral $latex \int_{1}^{8} \sqrt[3]{x} dx$.
Solution
Let’s find the integral of the expression by writing the cube root as a numerical exponent:
$$\int_{1}^{8} \sqrt[3]{x} dx=\int_{1}^{8} x^{\frac{1}{3}} dx$$
$$=\left[\frac{3}{4}x^{\frac{4}{3}} \right]_{1}^{8}$$
Evaluating the limits of integration, we have:
$$=\left[\frac{3}{4}(8)^{\frac{4}{3}} \right]-\left[\frac{3}{4}(1)^{\frac{4}{3}} \right]$$
We can simplify this by considering the exponent $latex \frac{4}{3}$ to be equivalent to taking the cube root of the number and raising the result to the fourth power:
$$=\left[\frac{3}{4}(16) \right]-\left[\frac{3}{4}(1) \right]$$
$$=12-\frac{3}{4}$$
$$=\frac{45}{4}=11~\frac{1}{4}$$
Definite integrals – Practice problems


Find the result of the following definite integral: $$\int_{1}^{4} 4x^3-6x^2+x^{-\frac{1}{2}} dx$$
Write the result in the input box.
See also
Interested in learning more about integrals of functions? You can look at these pages: