We can find the area between two curves by finding the area under each curve separately. Then, we can subtract these areas so that we get the area of the intersection. We can apply this principle not only with curves but also with the axes of the plane.
In this article, we will look at some solved exercises of the area between two curves. Then, we will look at some practice problems in which you can practice what you have learned.
How to find the area between two curves
Consider two intersecting curves, $latex f(x)$ and $latex g(x)$, as shown in the following diagram.
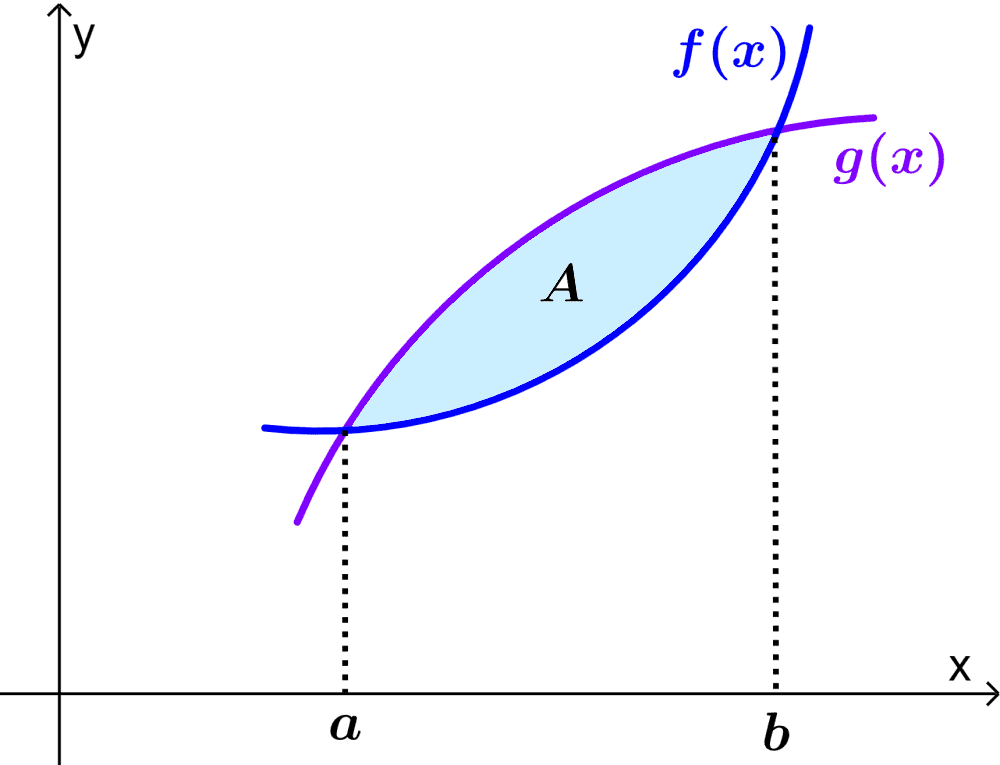
We can find the area of the colored region, that is, the region of intersection, by subtracting one curve from the other, so that the difference equals the area of intersection.
In this case, the area between the curves is obtained by subtracting the area under the curve $latex f(x)$ from the area under the curve $latex g(x)$. That is, we have the following:
$$A=\int_{a}^{b} g(x)dx-\int_{a}^{b} f(x)dx$$
$$A=\int_{a}^{b} (g(x)-f(x))dx$$
This principle can be applied to find the area between two or more curves, straight lines, or even axes.
Area between two curves – Examples with answers
EXAMPLE 1
If we have the curves $latex y=x^2+1$ and $latex y=-x^2+3$, what is the area between the curves?
Solution
We can start by finding the intersection points of the curves to determine the limits of the region. Then, we have:
$latex x^2+1=-x^2+3$
$latex 2x^2=2$
$latex x=\pm 1$
We can plot a graph to visualize the required area:
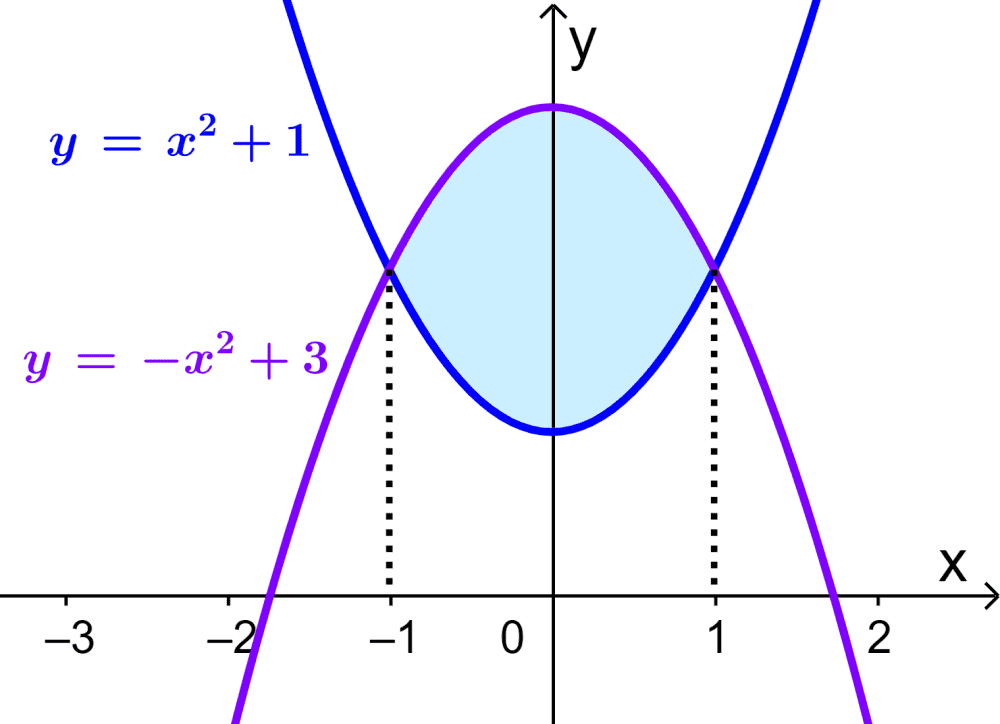
The area of the region can be obtained by subtracting the area under the curve $latex y=x^2+1$ from the area under the curve $latex y=-x^2+3$. Then, we have:
$$A=\int_{-1}^{1} (-x^2+3) dx-\int_{-1}^{1} (x^2+1) dx$$
$$=\int_{-1}^{1} (-x^2+3) – (x^2+1) dx$$
$$=\int_{-1}^{1} (-2x^2+2) dx$$
$$=\left[ -\frac{2x^3}{3}+2x \right]_{-1}^{1}$$
$$=\left[ -\frac{2}{3}+2 \right]-\left[ \frac{2}{3}-2 \right]$$
$$=\frac{4}{3}+\frac{4}{3}$$
$$=\frac{8}{3}$$
The area of the region of intersection of the two curves is $latex \frac{8}{3}$.
EXAMPLE 2
What is the area formed by the intersection of $latex y=-\frac{1}{3}x^2+3$ and the straight line $latex y=x+3$?
Solution
Similar to the previous example, we have to start by finding the intersection points of the line and the curve. Then, we have:
$latex x+3=-\frac{1}{3}x^2+3$
$latex \frac{1}{3}x^2+x=0$
$latex x(\frac{1}{3}x+1)=0$
$latex x=-3~~$ or $latex ~~x=0$
Now, we can plot a graph to visualize the required area:
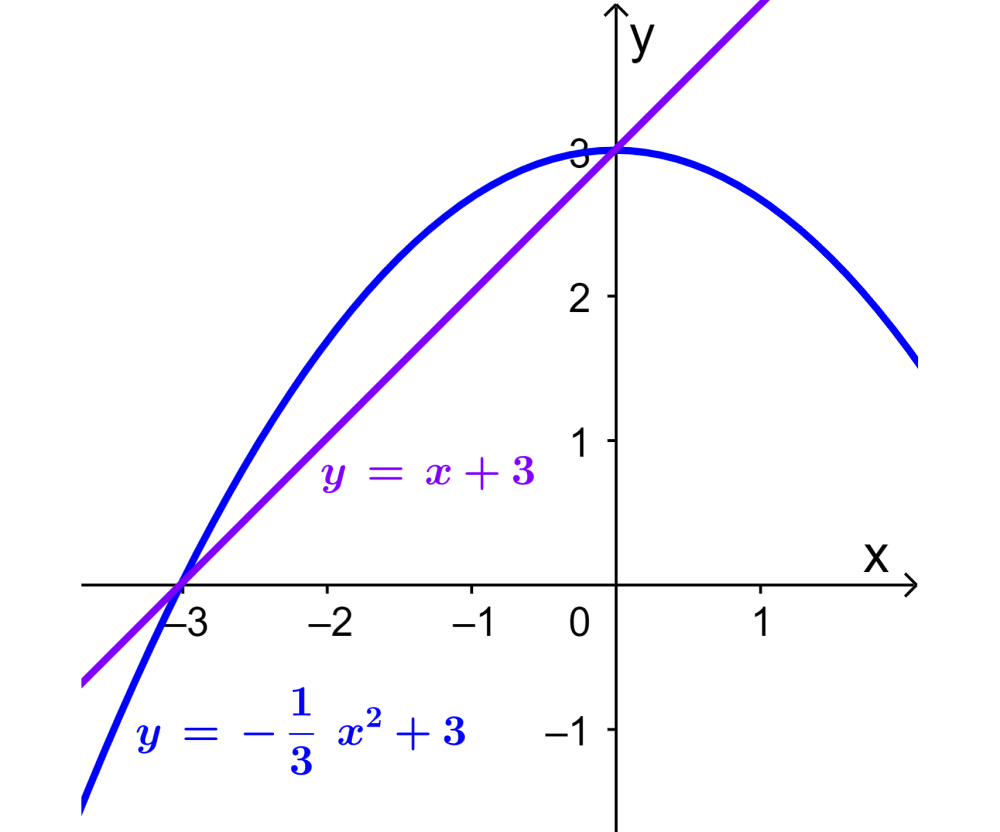
Then, we see that the area of the region is given by the area of the line minus the area of the curve. That is, we have:
$$A=\int_{-3}^{0} \left(-\frac{1}{3}x^2+3\right)dx-\int_{-3}^{0} (x+3 )dx $$
$$=\int_{-3}^{0} \left(-\frac{1}{3}x^2+3\right) – (x+3)dx$$
$$=\int_{-3}^{0} \left(-\frac{1}{3}x^2-x\right) dx$$
$$=\left[ -\frac{x^3}{9}-\frac{x^2}{2} \right]_{-3}^{0}$$
$$=\left[ -\frac{0^3}{9}-\frac{0^2}{2} \right]-\left[ -\frac{(-3)^3}{9}-\frac{(-3)^2}{2} \right]$$
$$=-\left[ 3-\frac{9}{2} \right]$$
$$=\frac{3}{2}$$
The area of the region of intersection of the two given curves is 1.5.
EXAMPLE 3
What is the area between the straight line $latex y=x+4$ and the curve $latex y=x^2-3x-1$?
Solution
Finding the intersection points of the straight line and the curve, we have:
$latex x+4=x^2-3x-1$
$latex x^2-4x-5=0$
$latex (x-5)(x+1)=0$
$latex x=5~~$ or $latex ~~x=-1$
When we plot a graph, we have the following:
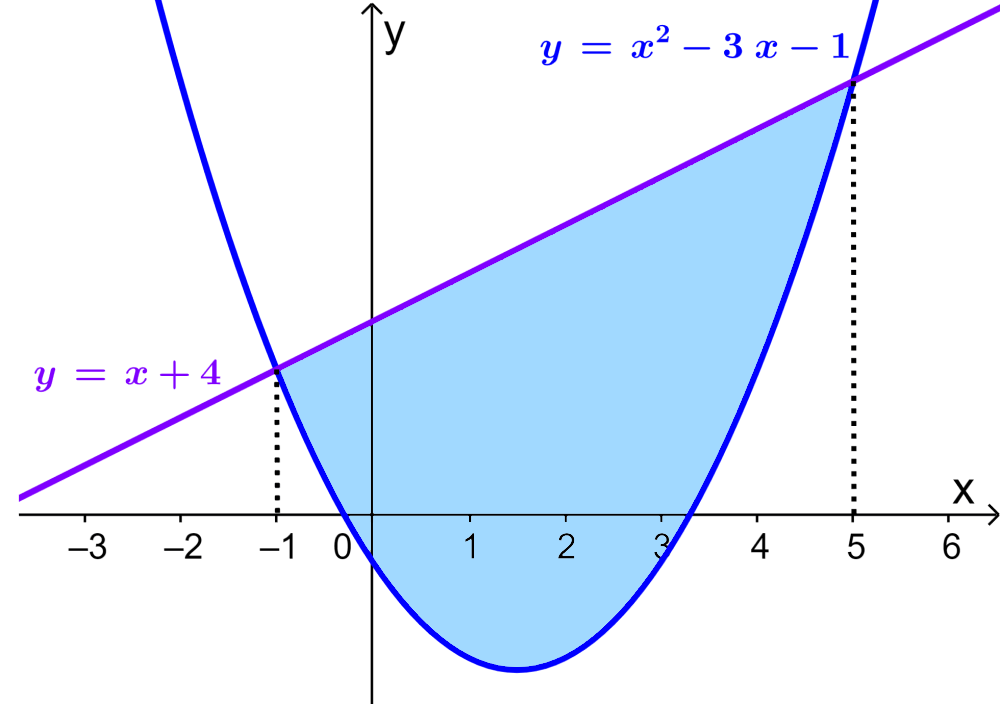
We can see that the required area is equal to the area under the line minus the area under the curve. Then, we have:
$$A=\int_{-1}^{5} (x+4 )dx-\int_{-1}^{5} (x^2-3x-1) dx$$
$$=\int_{-1}^{5} (x+4)- (x^2-3x-1) dx$$
$$=\int_{-1}^{5} (-x^2+4x+5) dx$$
$$=\left[ -\frac{x^3}{3}+2x^2+5x \right]_{-1}^{5}$$
$$=\left[ -\frac{(5)^3}{3}+2(5)^2+5(5) \right]-\left[ -\frac{(-1)^3}{3}+2(-1)^2+5(-1) \right]$$
$$=\left[ -\frac{125}{3}+50+25 \right]-\left[ \frac{1}{3}+2-5 \right]$$
$$=\frac{100}{3} +\frac{8}{3}$$
$$=\frac{108}{3} $$
$$=36$$
The area between the two given curves is 36.
EXAMPLE 4
If we have the curves $latex y=x^2+2x+2$ and $latex y=-x^2+2x+10$, what is the area of the intersection region?
Solution
We start by finding the intersection points:
$$x^2+2x+2=-x^2+2x+10$$
$latex 2x^2-8=2$
$latex x=\pm 2$
Plotting a graph, we have:
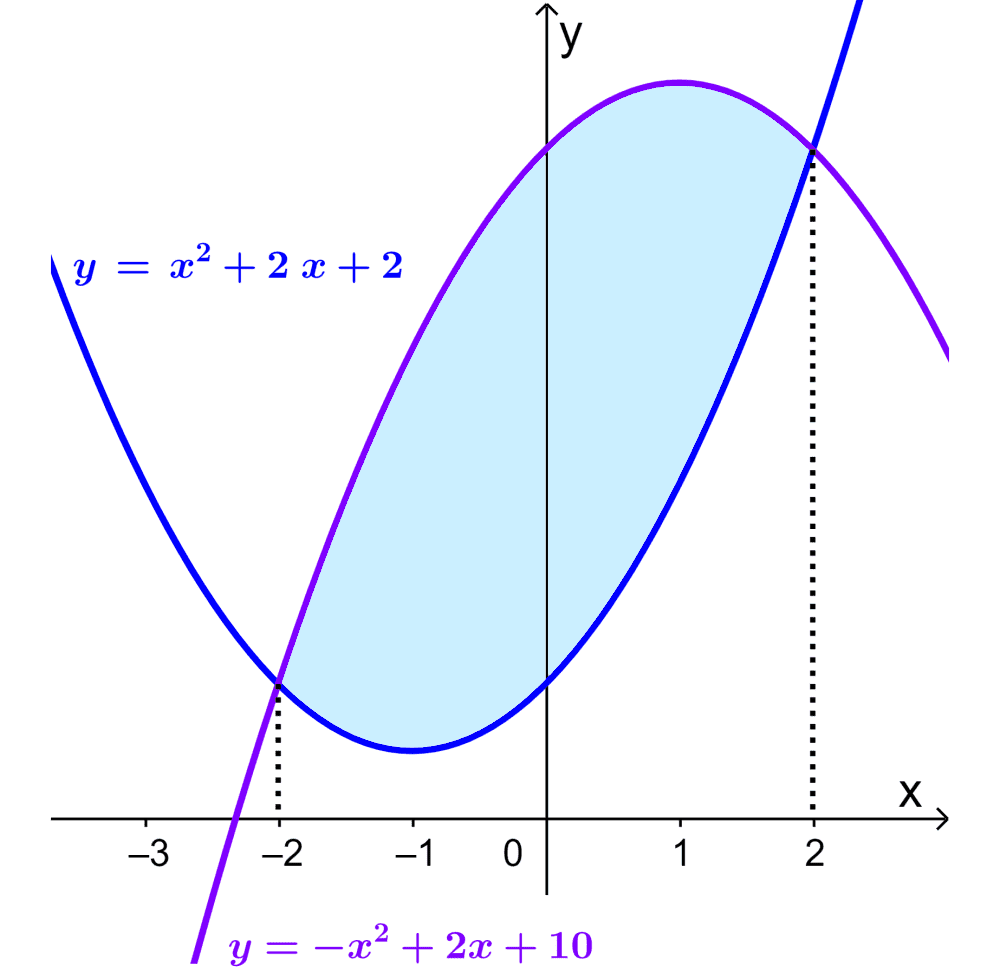
We can find the area of the required region as follows:
$$A=\int_{-2}^{2} (-x^2+2x+10) dx-\int_{-2}^{2} (x^2+2x+2) dx$$
$$=\int_{-2}^{2} (-x^2+2x+10) – (x^2+2x+2) dx$$
$$=\int_{-2}^{2} (-2x^2+8) dx$$
$$=\left[ -\frac{2x^3}{3}+8x \right]_{-2}^{2}$$
$$=\left[ -\frac{16}{3}-16 \right]-\left[ \frac{16}{3}-16 \right]$$
$$=\frac{32}{3}+\frac{32}{3}$$
$$=\frac{64}{3}$$
The area of the required region lying between the curves is $latex \frac{64}{3}$.
EXAMPLE 5
Find the area of the region of intersection of the curves $latex y=x^2+2$ and $latex y=-x^2+3$.
Solution
We start by finding the intersection points of the curves:
$latex x^2+2=-x^2+3$
$latex 2x^2=1$
$latex x=\pm \sqrt{0.5}$
When we plot a graph, we have:
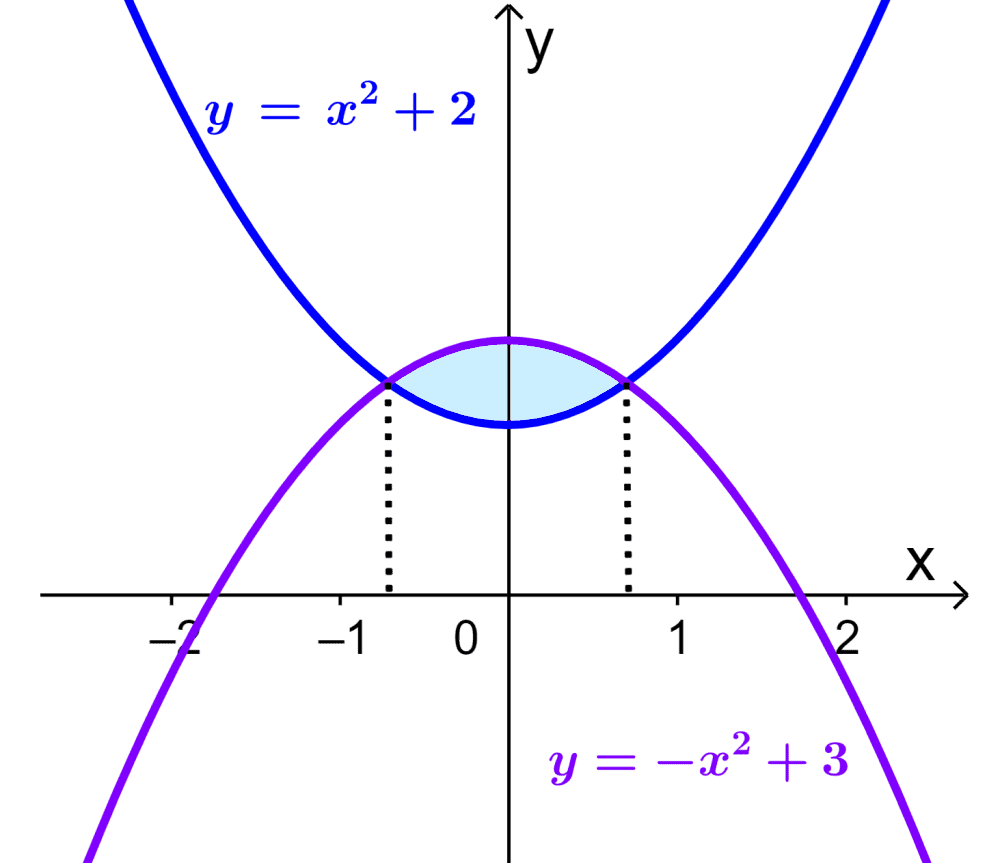
We can determine the area of the required region as follows:
$$A=\int_{-\sqrt{0.5}}^{\sqrt{0.5}} (-x^2+3) dx-\int_{\sqrt{0.5}}^{\sqrt{0.5}} (x^2+2) dx$$
$$=\int_{\sqrt{0.5}}^{\sqrt{0.5}} (-x^2+3) – (x^2+2) dx$$
$$=\int_{\sqrt{0.5}}^{\sqrt{0.5}} (-2x^2+1) dx$$
$$=\left[ -\frac{2x^3}{3}+x \right]_{-\sqrt{0.5}}^{\sqrt{0.5}}$$
$$=\left[ -\frac{\sqrt{0.5}}{3}+\sqrt{0.5} \right]-\left[ \frac{\sqrt{0.5}}{3}-\sqrt{0.5} \right]$$
$$=0.4714+0.4714$$
$$=0.9428$$
The area between the two given curves is $latex 0.9428$.
EXAMPLE 6
If we have the curve $latex y=x^2-2x-3$ and the straight line $latex y=x+1$, what is the area of the intersection region?
Solution
The intersection points are found as follows:
$latex x^2-2x-3=x+1$
$latex x^2-3x-4=0$
$latex (x-4)(x+1)=0$
$latex x=4~~$ or $latex ~~x=-1$
Then, we have the following graph:
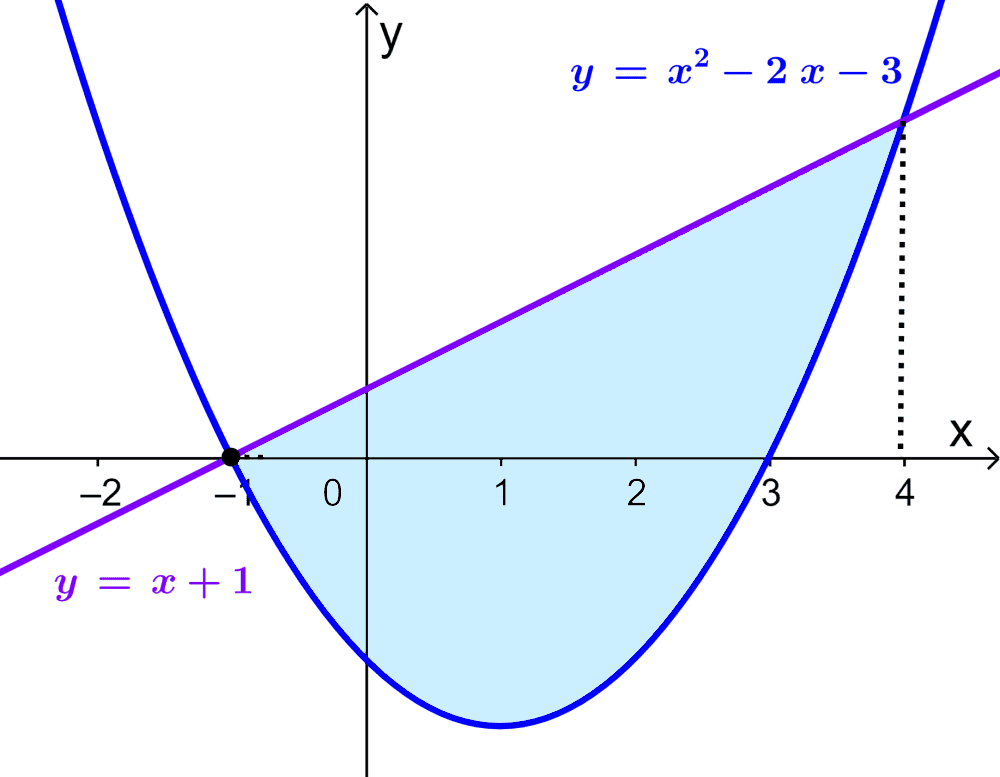
In this case, part of the required area is under the x-axis. However, the area of the region can be calculated using the same method. Then, we have:
$$A=\int_{-1}^{4} (x+1) dx-\int_{-1}^{4} (x^2-2x-3) dx$$
$$=\int_{-1}^{4} (x+1) – (x^2-2x-3) dx$$
$$=\int_{-1}^{4} (-x^2+3x+4) dx$$
$$=\left[ -\frac{x^3}{3}+\frac{3x^2}{2}+4x \right]_{-1}^{4}$$
$$=\left[ -\frac{64}{3}+24+16 \right]-\left[ \frac{1}{3}+\frac{3}{2}-4 \right]$$
$$=\frac{56}{3}+\frac{13}{6}$$
$$=\frac{125}{6}$$
The area of the required region is $latex \frac{125}{6}$.
EXAMPLE 7
Find the area between the curves $latex y=x^2-3$ and $latex y=\frac{1}{4}x^3-x+1$ ranging from $latex x=-2$ to $latex x=2$.
Solution
In this case, we don’t have to find the intersection points, since it is specified that we have to find the area from $latex x=-2$ to $latex x=2$.
By plotting a graph, we can visualize this area:
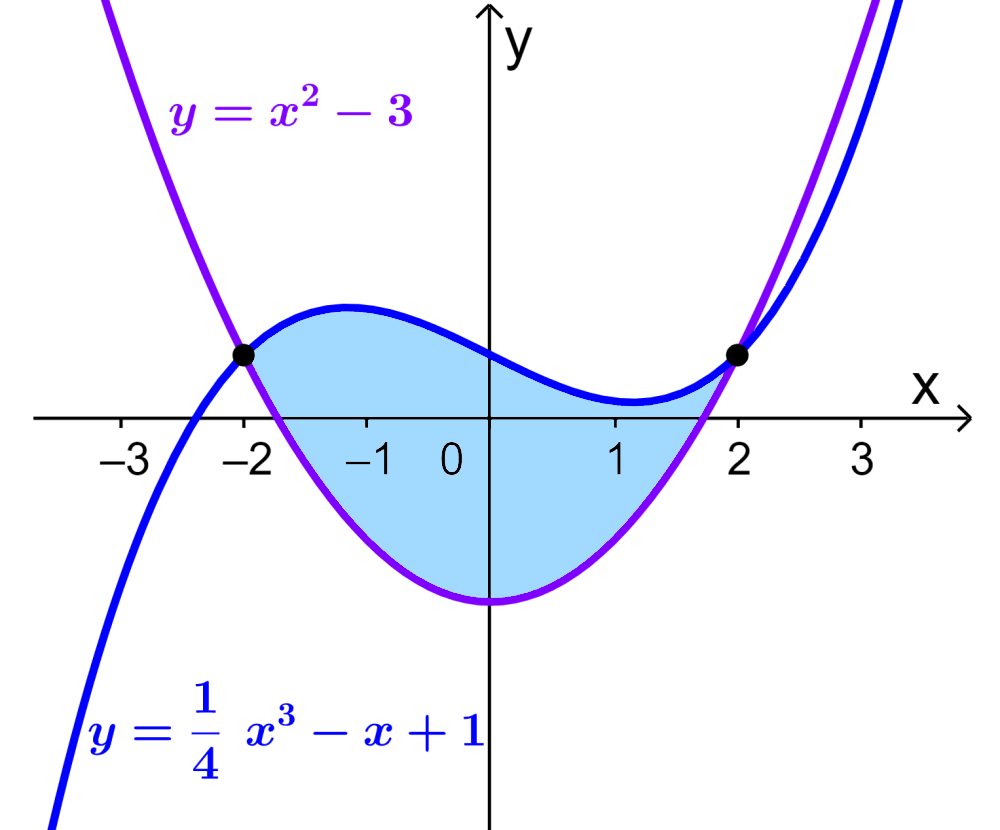
Now, we see that the required area is given by the area of the cubic curve minus the area of the quadratic curve:
$$A=\int_{-2}^{2} \left(\frac{1}{4}x^3-x+1\right)dx-\int_{-2}^{2} (x^2-3 )dx $$
$$=\int_{-2}^{2} \left(\frac{1}{4}x^3-x+1\right) – (x^2-3)dx$$
$$=\int_{-2}^{2} \left(\frac{1}{4}x^3-x^2-x+4\right) dx$$
$$=\left[ \frac{x^4}{16}-\frac{x^3}{3}-\frac{x^2}{2}+4x \right]_{-2}^{2}$$
$$=\left[ 1-\frac{8}{3}-2+8 \right]-\left[ 1+\frac{8}{3}-2-8 \right]$$
$$=\frac{13}{3}+\frac{19}{3}$$
$$=\frac{32}{3}$$
The area of the region of intersection of the two given curves is 10.67.
EXAMPLE 8
What is the area between the curves $latex y=-x^2+2$ and $latex y=\frac{1}{2}x^3-4x+2$ ranging from $latex x=0$ to $latex x=2$.
Solution
Similar to the previous example, we don’t have to find the intersection points, since we know the limits of integration. Then, plotting a graph, we have:
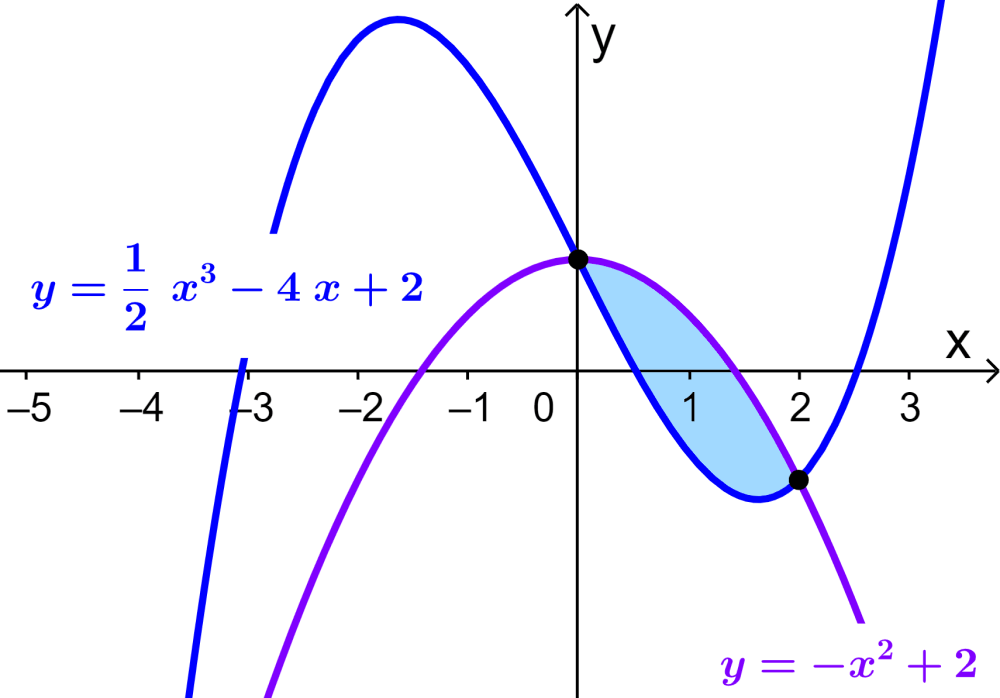
We see that the required area is equal to the area of the quadratic curve minus the area of the cubic curve:
$$A=\int_{0}^{2} \left(-x^2+2\right)dx-\int_{0}^{2} \left(\frac{1}{2}x^3-4x+2\right) dx$$
$$=\int_{0}^{2} \left(-x^2+2\right) – \left(\frac{1}{2}x^3-4x+2\right)dx$$
$$=\int_{0}^{2} \left(-\frac{1}{2}x^3-x^2+4x\right) dx$$
$$=\left[ -\frac{x^4}{8}-\frac{x^3}{3}+2x^2 \right]_{0}^{2}$$
$$=\left[ -2-\frac{8}{3}+8 \right]-\left[ 0 \right]$$
$$=\frac{10}{3}$$
The area of the region of intersection of the two given curves is 3.33.
Area between two curves – Practice problems
Find the area between the curves $latex y=\pm \sqrt{2x+6}$ and $latex y=x-1$.
Write the answer in the input box.
See also
Interested in learning more about integrals of functions? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
