The volume of revolution about the x-axis can be found by evaluating a definite integral with respect to the square of the equation of the curve and multiplying the result by π. We can derive a formula to calculate this volume using limits and integrals.
In this article, we will learn how to calculate the volume of revolution with respect to the x-axis. We will learn how to derive its formula and use it in some practice problems.
CALCULUS
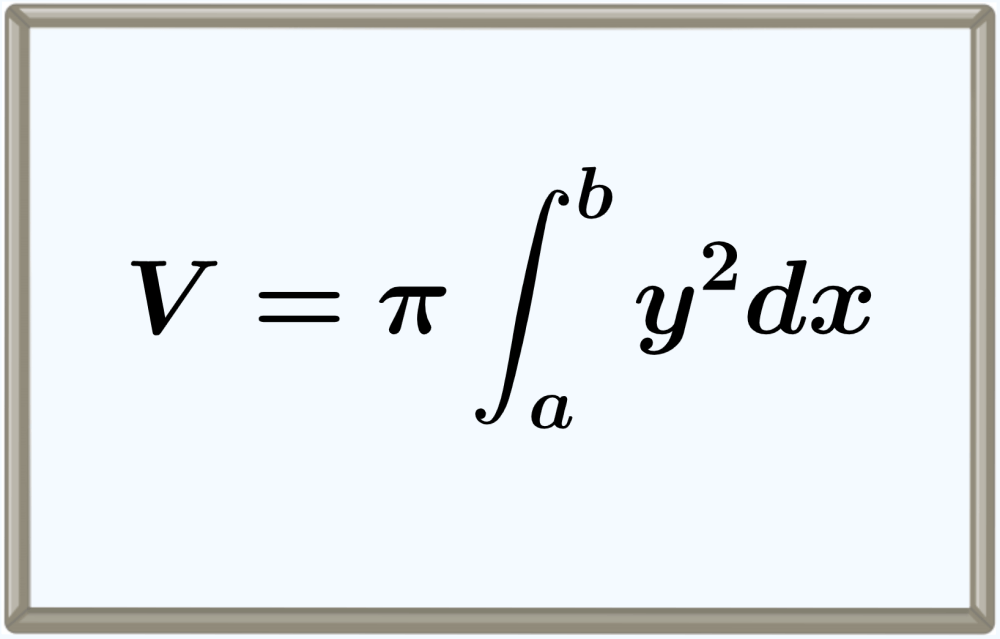
Relevant for…
Learning how to calculate the volume of revolution about the x-axis.
CALCULUS
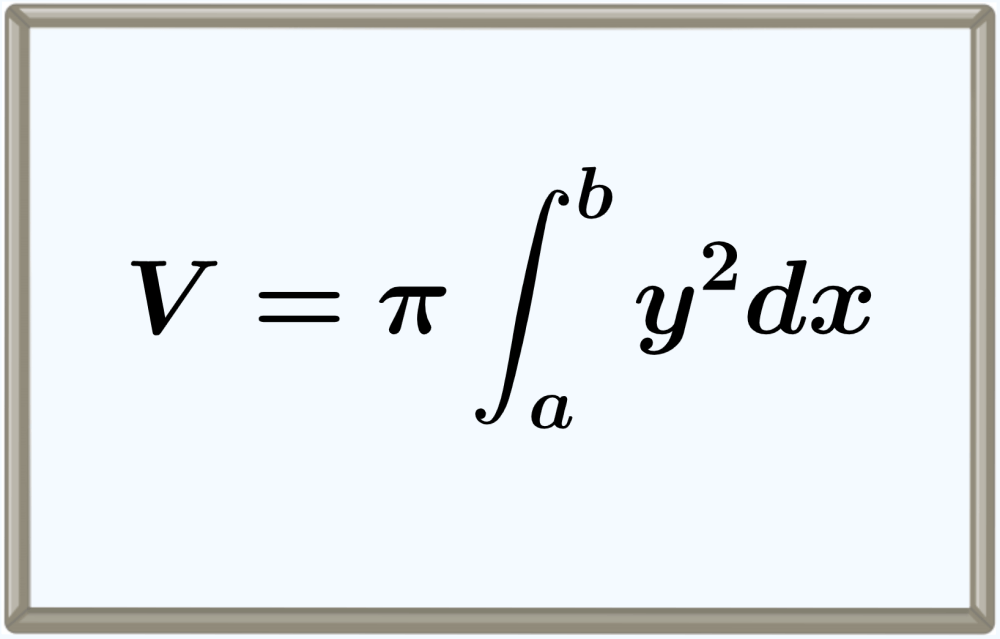
Relevant for…
Learning how to calculate the volume of revolution about the x-axis.
How to find the volume of revolution about the x-axis
To find the volume of revolution of a solid with respect to the x-axis, we can apply the following formula:
$$V=\pi \int_{a}^{b} y^2 d x$$
Then, we can follow the following process to use the formula correctly:
1. Find the square of the equation of the curve that forms the volume of revolution.
That is, we start by finding $latex y^2$.
2. Find the value of the definite integral $latex \int_{a}^{b} y^2 d x$.
For this, we substitute the expression for $latex y^2$ from step 1.
3. Multiply the result from step 2 by π to find the volume of the solid formed.
If you need to review how to solve definite integrals, you can visit our article: How to calculate definite integrals.
Proof of the formula for the volume of revolution about the x-axis
To find a formula for the volume of revolution about the x-axis, we start by considering the area under the curve $latex y=x^2$ from $latex x=1$ to $latex x=2$, as shown in the diagram:
Now, we consider the solid formed when this area is rotated 2π radians around the x-axis, as shown in the diagram below. We can calculate its volume using integral calculus.
We take a very small strip of length $latex x$ under the curve $latex f(x)$, as shown in the following diagram:
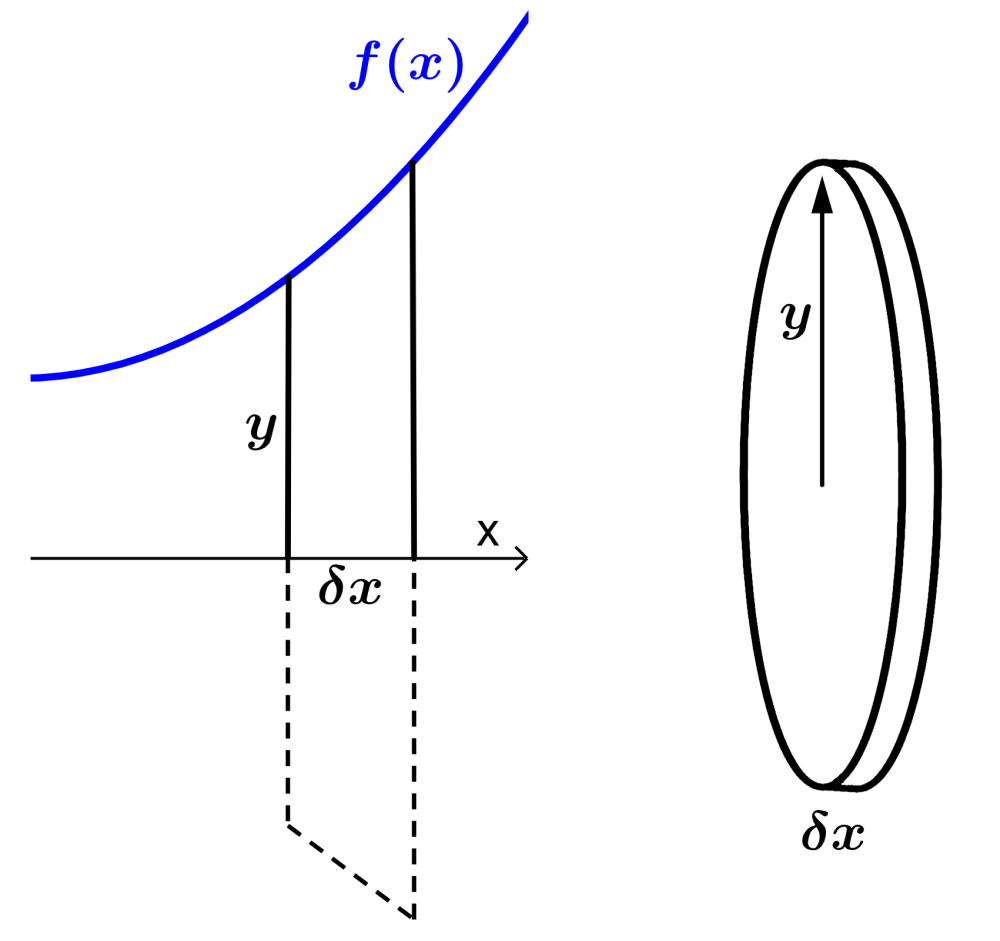
When this small area is rotated by 2π radians around the x-axis, we form a disk with a radius equal to $latex y$ and a width of $latex \delta x$. The volume of this disk is:
$latex \delta V= \pi y^2 \delta x$.
To find the volume of the whole solid, we have to find the sum of all the disks from $latex x=a$ to $latex x=b$. Then, we have:
$$V=\sum_{x=a}^{b}\pi y^2 \delta x$$
As $latex \delta \to 0$, this summation approaches the value of $latex V$, so we have:
$$V=\lim_{\delta x \to 0} \pi \sum_{x=a}^{b} y^2 \delta x$$
which is equal to
$$V=\pi \int_{a}^{b} y^2 d x$$
Volume of revolution about the x-axis – Examples with answers
EXAMPLE 1
Find the volume generated when the area under $latex y=x$ from $latex x=0$ to $latex x=6$ is rotated about the x-axis.
Solution
We begin by writing the formula for the volume of revolution:
$$V=\pi \int_{a}^{b} y^2 d x$$
Now, we substitute the expression for $latex y$, square it and solve the definite integral:
$$V=\pi \int_{0}^{6} x^2 d x$$
$$=\pi \left[ \frac{x^3}{3} \right]_{0}^{6}$$
$$=\pi \left( \frac{216}{3} \right)-(0)$$
$latex V=72 \pi $
EXAMPLE 2
What is the volume generated when the area under $latex y=x^2$ from $latex x=0$ to $latex x=5$ is rotated with respect to the x-axis?
Solution
The formula for the volume of revolution with respect to the x-axis is:
$$V=\pi \int_{a}^{b} y^2 d x$$
In this case, we have $latex y=x^2$, so we substitute into the formula and evaluate the definite integral:
$$V=\pi \int_{0}^{5} x^4 d x$$
$$=\pi \left[ \frac{x^5}{5} \right]_{0}^{5}$$
$$=\pi \left( \frac{3125}{5} \right)-(0)$$
$latex V=625 \pi $
EXAMPLE 3
Find the volume of the solid formed when the area under $latex y=x^2+2$ from $latex x=1$ to $latex x=3$ is rotated about the x-axis.
Solution
The volume of the solid is given by the following formula:
$$V=\pi \int_{a}^{b} y^2 d x$$
By squaring $latex y$, we have $latex y^2=(x^2+2)^2$, which is equal to $latex y^2=x^4+4x^2+4$. Then, we have:
$$V=\pi \int_{1}^{3} (x^4+4x^2+4) d x$$
$$=\pi \left[ \frac{x^5}{5} + \frac{4x^3}{3}+4x \right]_{1}^{3}$$
$$=\pi \left( \frac{483}{5}- \frac{83}{15} \right)$$
$$ V=\frac{1366 \pi}{15} $$
EXAMPLE 4
Find the volume of revolution of the area under $latex y=3\sqrt{x}$ from $latex x=2$ to $latex x=4$ about the x-axis.
Solution
We start with the following formula to find the volume:
$$V=\pi \int_{a}^{b} y^2 d x$$
When we square $latex y$, we get $latex y^2=9x$. Then, we use this in the formula to solve the definite integral:
$$V=\pi \int_{2}^{4} 9x d x$$
$$=\pi \left[ \frac{9x^2}{2} \right]_{2}^{4}$$
$latex =\pi (72 )-( 18)$
$latex V=54\pi $
EXAMPLE 5
Find the volume of revolution when the area under $latex y=\sqrt{x^2+3x}$ from $latex x=2$ to $latex x=6$ is rotated about the x-axis.
Solution
We begin by writing the formula for the volume of revolution about the x-axis:
$$V=\pi \int_{a}^{b} y^2 d x$$
When we square $latex y$, we have $latex y^2=(\sqrt{x^2+3x})^2$, which is equal to $latex y^2=x^2+3x$. Then, we have:
$$V=\pi \int_{2}^{6} (x^2+3x) d x$$
$$=\pi \left[ \frac{x^3}{3} + \frac{3x^2}{2} \right]_{2}^{6}$$
$$=\pi [72 + 54 ]-\left[ \frac{8}{3} + 6 \right]$$
$$=\pi \left( \frac{352}{3} \right)$$
$$ V=\frac{352\pi}{3} $$
EXAMPLE 6
The area enclosed between the curve $latex y=4-x^2$ and the straight line $latex y=4-2x$ is rotated with respect to the x-axis. Find the volume of the generated solid.
Solution
In this case, we have an area between two curves. Then, we can plot a simple graph to visualize that area:
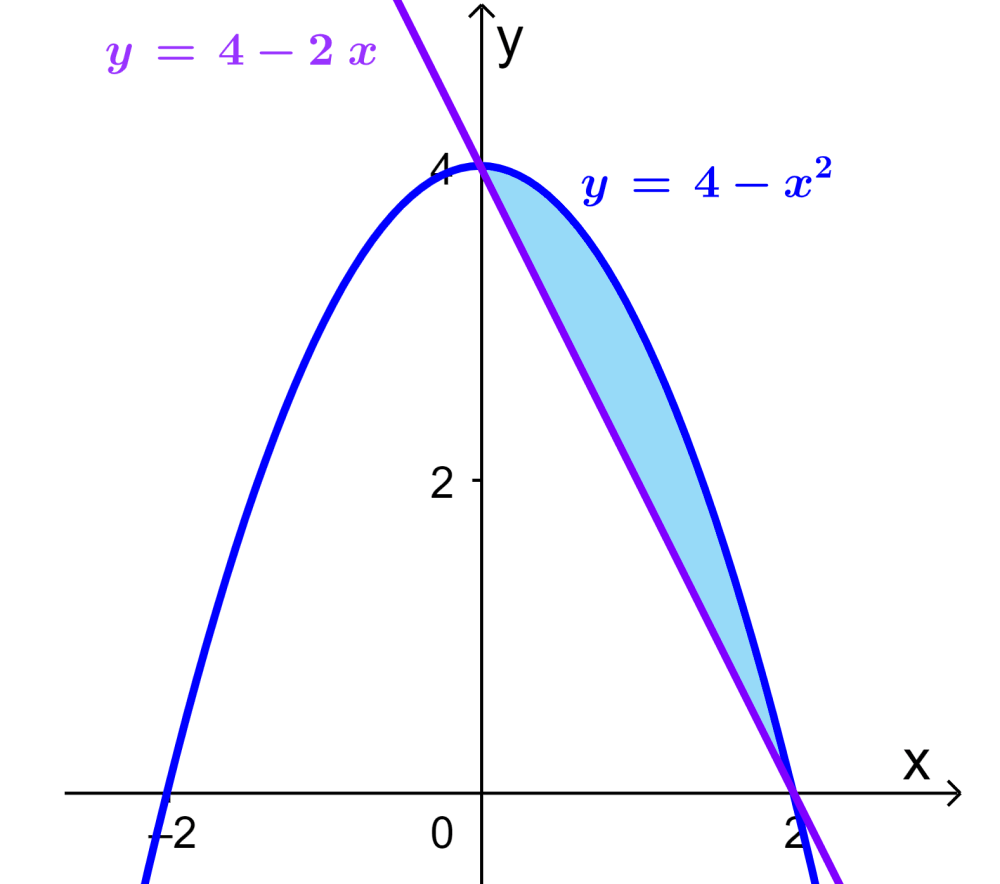
Now, we can see that the area to be rotated is an area between two curves. Therefore, we solve as follows:
$$V=\pi \int_{0}^{2} (4-x^2)^2 d x-\pi \int_{0}^{2} (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (4-x^2)^2 – (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (x^4-12x^2+16x) d x$$
$$=\pi \left[ \frac{x^5}{5}-4x^3+8x^2 \right]_{0}^{2}$$
$$=\pi \left[ \frac{32}{5}-32+32 \right]-[0]$$
$latex V=\frac{32\pi}{5} $
Volume of revolution about the x-axis – Practice problems
What is the volume of revolution of the area under $latex y=\sqrt{3x^2+8}$ from $latex x=1$ to $latex x=3$ with respect to the x axis? ?
Write the answer in the input box.
See also
Interested in learning more about integrals of functions? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
