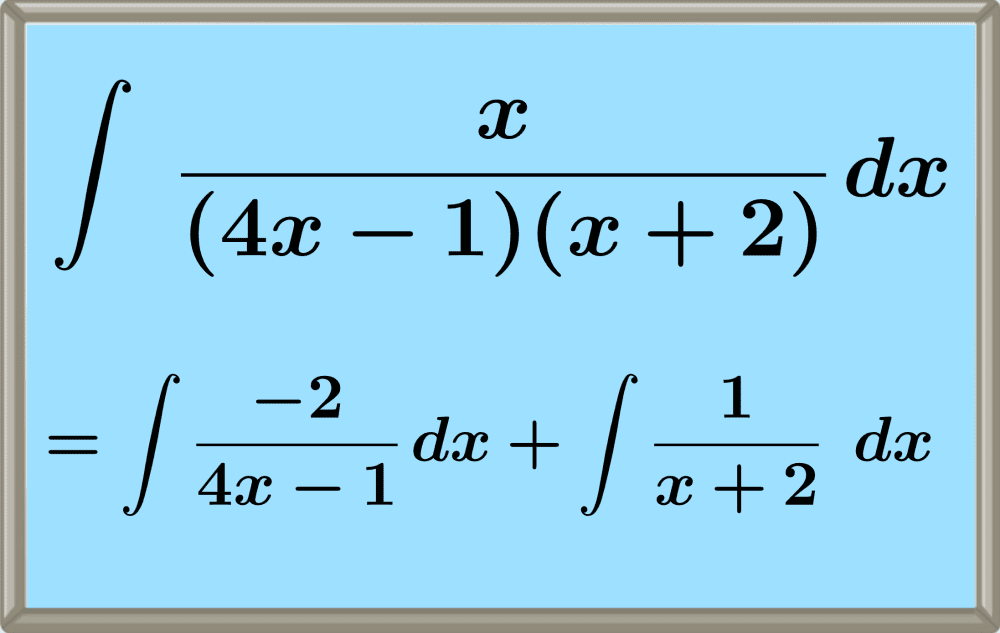Integration by Partial Fractions – Examples with Answers

This case corresponds to an integrand of the form $latex \frac{P(x)}{Q(x)}$ where the degree of $latex P(x)$ is greater than or equal to the degree of $latex Q(x) )$.

In such a case, the first thing to do is perform the division of polynomials. In this way, the quotient $latex \frac{P(x)}{Q(x)}$ is expressed as:

$$ \dfrac{P(x)}{Q(x)}=q(x)+\dfrac{r(x)}{Q(x)}$$

Where $latex q(x)$ is the quotient and $latex r(x)$ is the remainder. For the integrand of the example, we obtain:

$$ (x^2+x+3)\,\div\, (x-2)= (x+3) + \dfrac{9}{x-2}$$

With this in mind, the integral to be solved is rewritten as follows:

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\int \left[(x+3) + \frac{9}{x-2}\right]dx$$

Obtaining three immediate integrals:

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\int x\,dx+3\int dx +9\int \frac{dx}{x-2}$$

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\frac{x^2}{2}+3x +9\ln|x-2|+C$$

Since the degree of the denominator is greater than the degree of the numerator, it is not necessary to divide, and we go directly to factoring the denominator, which is very simple since it is a difference of perfect squares:

$$x^2-9=(x+3)(x-3)$$

Thus, the proposed integral would be as follows:

$$\int \frac{dx}{x^2-9}=\int \frac{dx}{(x+3)(x-3)}$$

Since the denominator is the product of two linear factors, the integrand can be expressed in this way:

$$ \frac{dx}{x^2-9}=\frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

Solving the sum of algebraic fractions, results:

$$ \frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

$$=\frac{A(x-3)+B(x+3)}{(x+3)(x-3)}$$

$$=\frac{Ax-3A+Bx+3B}{(x+3)(x-3)}$$

$$=\frac{x(A+B)-3A+3B}{(x+3)(x-3)}$$

Since the denominator is always the same, we have:

$$x(A+B)-3A+3B = 1$$

Equating the respective coefficients of each power of $latex x$, leads to the following equations:

$latex \phantom{-3}A+\phantom{3}B=0$

$latex -3A+3B=1$

Adding both equations term by term, we deduce that:

$latex 2B=1\Rightarrow B=\dfrac{1}{2}$

Since $latex A=-B$, then:

$latex A=-\dfrac{1}{2}$

Therefore:

$$ \frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

$$=-\frac{1}{2}\left(\frac{1}{x+3}\right)+\frac{1}{2}\left(\frac{1}{x-3}\right)$$

And the integral sought is transformed into:

$$\int \frac{dx}{x^2-9}=-\frac{1}{2}\int\frac{dx}{x+3}+\frac{1}{2}\int\frac{dx}{x-3}$$

$$=-\frac{1}{2}\ln\left|\frac{1}{x+3}\right|+\frac{1}{2}\ln\left|\frac{1}{x-3}\right| +C$$

Therefore:

$$\int \frac{dx}{x^2-9}=-\frac{1}{2}\ln\left|\frac{1}{x+3}\right|+\frac{1}{2}\ln\left|\frac{1}{x-3}\right| +C$$

The degree of the numerator is less than the degree of the denominator, therefore, the denominator is factored, which turns out to be the cube of a sum:

$$x^3+3x^2+3x+1=(x+1)^3$$

The integral is then written with the denominator already factored:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=\int\frac{3x+2}{(x+1)^3}dx$$

Note that the denominator consists of a single linear factor that is raised to the cube, whose form is $latex (px+q)^m$, with $latex m=3$.

In such a case, the decomposition into simple fractions of the integrand takes the following form:

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{3x+2}{(x+1)^3}=\frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{(x+1)^3}$$

And now we follow a similar process as in the previous example, in order to find the coefficients $latex A$, $latex B$ and $latex C$:

$$\frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{(x+1)^3}=\frac{A(x+1)^2+B(x+1)+C}{(x+1)^3}$$

Then, the numerator is carefully developed:

$$A(x+1)^2+B(x+1)+C =A(x^2+2x+1)+Bx+B+C$$

$$Ax^2+2Ax+A+Bx+B+C=Ax^2+(2A+B)x+B+C=3x+2$$

By equating the coefficients of the equal powers on both sides of the equality, the following equations are obtained:

$latex A=0$

$latex 2A+B=3\Rightarrow B=3$

$latex B+C=2\Rightarrow C=-1$

With these values, the integrand is as follows:

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{0}{x+1}+\frac{3}{(x+1)^2}-\frac{1}{(x+1)^3}$$

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{3}{(x+1)^2}-\frac{1}{(x+1)^3}$$

Now the original integral is transformed into the sum of two easily solved integrals through a simple change of variable:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{dx}{(x+1)^2}-\int\frac{dx}{(x+1)^3}$$

The change of variable is $latex u =x+1$, $latex du=dx$:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{du}{u^2}-\frac{du}{u^3}$$

Applying the power rule for integration, we obtain:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{du}{u^2}-\frac{du}{u^3}$$

$$=3\int u^{-2}du-\int u^{-3}du$$

$$=\frac{3u^{-1}}{(-1)}-\frac{u^{-2}}{(-2)}+C=-\frac{3}{x+1}+\frac{1}{2(x+1)^{2}}+C$$

Finally:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=-\frac{3}{x+1}+\frac{1}{2(x+1)^{2}}+C$$

It is observed that the degree of the denominator is greater than that of the numerator, so the denominator is factored:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\int\frac{x^2+2x-1}{x(x^2+x-2)}dx$$

The trinomial $latex x^2+x-2$ can be easily factored:

$$x^2+x-2=(x+2)(x-1)$$

Which is substituted in the denominator of the integrand:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\int\frac{x^2+2x-1}{x(x^2+x-2)}dx$$

$$=\int\frac{x^2+2x-1}{x(x+2)(x-1)}dx$$

Since there are linear factors in the denominator, the algebraic fraction can be expressed as follows:

$$\frac{x^2+2x-1}{x(x+2)(x-1)}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}$$

Where the coefficients $latex A$, $latex B$ and $latex C$ are real numbers to be determined by simple algebra:

$$\frac{x^2+2x-1}{x(x+2)(x-1)}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}$$

$$=\frac{A(x+2)(x-1)+Bx(x-1)+Cx(x+2)}{x(x+2)(x-1)}$$

$$=\frac{A( x^2+x-2)+B(x^2-x)+C(x^2+2x)}{x(x+2)(x-1)}$$

$$=\frac{ x^2(A+B+C)+x(A-B+2C)-2A}{x(x+2)(x-1)}$$

Which results in the following:

$$x^2(A+B+C)+x(A-B+2C)-2A =x^2+2x-1$$

Equalizing the coefficients of the similar powers, we obtain the following equations:

$latex A+B+C=1$

$latex A-B+2C=2$

$latex-2A=-1$

From the latter, it is easy to deduce that:

$latex A = \dfrac{1}{2}$

And adding the first two equations, $latex B$ cancels and leaves:

$latex 2A+3C=3$

Substituting $latex A = \dfrac{1}{2}$ here, results in:

$latex 2\left(\frac{1}{2}\right)+3C=3$

$latex 1+3C=3$

$latex 3C=2$

$latex C = \dfrac{2}{3}$

Knowing the values of $latex A$ and $latex C$, the value of $latex B$ is removed from any of the equations in which it appears:

$$A+B+C=1\Longrightarrow B=1-A-C=1-\dfrac{1}{2}-\dfrac{2}{3}=\dfrac{1}{6}$$

$latex B= -\dfrac{1}{6}$

Once the coefficients are obtained, they are substituted in the integral as follows:

$$\int\frac{x^2+2x-1}{x(x+2)(x-1)}dx=\int\left[\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}\right]dx$$

$$=\int\left[\frac{1}{2x}-\frac{1}{6(x+2)}+\frac{2}{3(x-1)}\right]dx$$

$$=\int\frac{dx}{2x}-\int\frac{dx}{6(x+2)}+\int\frac{2dx}{3(x-1)}$$

$$=\frac{1}{2}\ln|x|-\frac{1}{6}\ln|x+2|+\frac{2}{3}\ln|x-1|+C$$

Therefore:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\frac{1}{2}\ln|x|-\frac{1}{6}\ln|x+2|+\frac{2}{3}\ln|x-1|+C$$

In this case, the denominator is already factored, and consists of a linear factor and a quadratic and irreducible factor. When this happens, the decomposition into simple fractions looks like this:

$$\frac{2}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}$$

Following a similar process to that of the previous examples, the addition of fractions is carried out:

$$\frac{A(x^2+1)+(x-1)(Bx+C)}{(x-1)(x^2+1)}=\frac{Ax^2+A+Bx^2-Bx+Cx-C}{(x-1)(x^2+1)}$$

$$=\frac{(A+B)x^2+(-B+C)x+A-C}{(x-1)(x^2+1)}=\frac{2}{(x-1)(x^2+1)}$$

Forming an equation with the numerators, we have:

$$(A+B)x^2+(-B+C)x+A-C=2$$

The system of three equations with three unknowns is obtained:

$latex \phantom{-}A+B=0\\-B+C=0\\\phantom{-}A-C=2\\$

And its solution is: $latex A=1$, $latex B=-1$, $latex C=-1$.

Thus, the algebraic fraction becomes:

$$\frac{2}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}$$

$$\frac{1}{x-1}+\frac{(-x-1)}{x^2+1}=\frac{1}{x-1}-\frac{(x+1)}{x^2+1}$$

And the integral results in:

$$\int\frac{2}{(x-1)(x^2+1)}dx=\int\frac{dx}{x-1}-\int\frac{xdx}{x^2+1}-\int\frac{dx}{x^2+1}\Rightarrow$$

$$\int\frac{2}{(x-1)(x^2+1)}dx=\ln\left|x-1\right|-\frac{1}{2}\ln(x^2+1)-\arctan x+C$$

In the denominator of this integral appears a polynomial of 3rd degree, which can be factored by Ruffini’s method.

$$\begin{array}{r|rrrr}  & 1 & 0 & -2 & -4\\ 2 &  & 2 & 4 & 4\\ \hline  & 1 & 2 & 2 & 0\end{array}$$

The resulting polynomial cannot be factored, so the denominator looks like this:

$$x^3-2x-4 = (x-2)(x^2+2x+2)$$

Then, the integrand is rewritten as:

$$\int\frac{3x+4}{x^3-2x-4}dx=\int\frac{3x+4}{(x-2)(x^2+2x+2)}dx$$

Since the denominator consists of a linear factor and a quadratic and irreducible factor, the algebraic fraction can be decomposed in this way:

$$\frac{3x+4}{x^3-2x-4}=\frac{A}{(x-2)}+\frac{Bx+C}{(x^2+2x+2)}$$

$$=\frac{A(x^2+2x+2)+(Bx+C)(x-2)}{(x-2)(x^2+2x+2)}$$

$$=\frac{Ax^2+2Ax+2A+Bx^2-2Bx+Cx-2C}{(x-2)(x^2+2x+2)}$$

$$=\frac{(A+B)x^2+(2A-2B+C)x+2A-2C}{(x-2)(x^2+2x+2)}$$

Forming an equation with the numerators:

$$(A+B)x^2+(2A-2B+C)x+2A-2C=3x+4$$

The system of equations is obtained:

$$\phantom{2}A+\phantom{2}B\phantom{+C} = 0\\ 2A-2B+C = 3\\ 2A\phantom{-2B}-C = 4\\$$

That has this solution: $latex A=1$, $latex B=-1$, $latex C=-1$.

The proposed integral is rewritten as follows:

$$\int\frac{3x+4}{x^3-2x-4}dx=\int\left[\frac{1}{x-2}+\frac{-x-1}{x^2+2x+2}\right]dx$$

$$=\int\frac{dx}{x-2}-\int\frac{(x+1)dx}{x^2+2x+2}$$

The first integral is direct:

$$\int\frac{dx}{x-2}=\ln|x-2|+C$$

The second is easily solved through a change of variable:

$latex u = x^2+2x+2$

$latex du = (2x+2)dx=2(x+1)dx$

$$\int\frac{(x+1)dx}{x^2+2x+2}=\int\frac{du}{2u}+C=\frac{1}{2}\ln|x^2+2x+2|+C$$

Putting both results together:

$$\int\frac{3x+4}{x^3-2x-4}dx=\ln|x-2|-\frac{1}{2}\ln|x^2+2x+2|+C$$

At first glance, it does not seem that the method of simple fractions is applicable, however, the following change of variable makes it possible:

$latex u =e^t$

$latex du=e^t dt$

Thus, the integral is rewritten as:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\int \frac {du}{u^2+3u+2}$$

The denominator is factored as:

$$u^2+3u+2=(u+2)(u+1)$$

And the integral is expressed as follows:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\int \frac {du}{u^2+3u+2}=\int\frac {du}{(u+2)(u+1)}$$

Immediately, the integrand is written as:

$$\frac {1}{(u+2)(u+1)}=\frac {A}{u+2}+\frac{B}{u+1}$$

$$=\frac {A(u+1)+B(u+2)}{(u+2)(u+1)}=\frac {Au+A+Bu+2B}{(u+2)(u+1)}$$

$$=\frac {u(A+B)+A+2B}{(u+2)(u+1)}$$

The system of equations obtained by equating the numerators is:

$latex A+\phantom{2}B=0\\A+2B=1\\$

And its solution is: $latex A= -1$, $latex B =1 $.

Therefore:

$$\int\frac {du}{(u+2)(u+1)}=-\int \frac{du}{x+2}+\int \frac{du}{x+1}$$

$$=-\ln|u+2|+\ln|u+1|+C$$

$$=\ln\left| \frac{u+1}{u+2}\right|+C$$

Finally, returning the change of variable made at the beginning, we have:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\ln\left( \frac{e^t+1}{e^t+2}\right)+C$$

As in the previous case, it is convenient to change the variable:

$latex u = \cos x$

$latex du=-\sin x dx$

In this way:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=\int\frac{-du}{u(u-1)}=-\int\frac{du}{u(u-1)}$$

The integrand becomes:

$$\frac{1}{u(u-1)}=\frac{A}{u}+\frac{B}{u-1}=\frac{A(u-1)+Bu}{u(u-1)}$$

$$=\frac{Au-A+Bu}{u(u-1)}=\frac{u(A+B)-A}{u(u-1)}$$

The resulting system of equations is:

$latex A+B=0\\\phantom{+}-A=1\\$

Then: $latex A =-1 $, $latex B =1 $.

The original integral becomes:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=-\left[\int\frac{-du}{u}+\int\frac{du}{u-1}\right]$$

$$=\ln|u|-\ln|u-1|+C=\ln\left| \frac{u}{u-1}\right|+C$$

Therefore:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=\ln\left| \frac{\cos x}{\cos x-1}\right|+C$$

As always, the first step is to find the factorization of the denominator:

$$x^4+4x^2+3=u^2+4u+3$$

With $latex u=x^2$, we have:

$$u^2+4u+3=(u+3)(u+1)=(x^2+3)(x^2+1)$$

Therefore:

$$\frac{x^3+x^2+x+3}{x^4+4x^2+3}=\frac{Ax+B}{x^2+3}+\frac{Cx+D}{x^2+1}=$$

$$\frac{(Ax+B)(x^2+1)+(Cx+D)(x^2+3)}{(x^2+1)(x^2+3)}=$$

$$\frac{(Ax^3+Ax+Bx^2+B)+(Cx^3+3Cx+Dx^2+3D)}{(x^2+1)(x^2+3)}=$$

$$\frac{(A+C)x^3+(B+D)x^2+(A+3C)x+B+3D}{(x^2+1)(x^2+3)}$$

The following equations are obtained:

$latex A + \phantom{3}C = 1\\B +\phantom{3}D= 1\\A+3C=1\\B+3D=3\\$

Subtracting the third equation from the first one, we obtain:

$latex 2C=0\Rightarrow C=0$

$latex A=1$

And subtracting the fourth from the second:

$latex 2D=2\Rightarrow D =1$

$latex B=0$

Then:

$$\frac{x^3+x^2+x+3}{x^4+4x^2+3}=\frac{x}{x^2+3}+\frac{1}{x^2+1}$$

And the integral becomes:

$$\int\frac{x^3+x^2+x+3}{x^4+4x^2+3}dx=\int\frac{x}{x^2+3}dx+\int\frac{1}{x^2+1}dx$$

Since the degree of the numerator is greater than the degree of the denominator, it is necessary to first perform the division of polynomials and then apply the division algorithm:

$$ (x^4-6x^3+12x^2+6)\,\div\, (x^3-6x^2+12x-8)=$$

$$= x + \dfrac{8x+6}{x^3-6x^2+12x-8}$$

The denominator of the algebraic fraction is the cube of a difference, so it is factored like this:

$$x^3-6x^2+12x-8=(x-2)^3$$

All of the above leads to:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\int xdx+\int \frac{8x+6}{x^3-6x^2+12x-8}dx=$$

$$=\int xdx+\int\frac{8x+6}{(x-2)^3}dx$$

The integrand of the second integral is decomposed into simple fractions as follows:

$$\frac{8x+6}{(x-2)^3}=\frac{A}{(x-2)}+\frac{B}{(x-2)^2}+\frac{C}{(x-2)^3}$$

Solving the sum of fractions on the right-hand side and forming an equation with the numerators, we have:

$latex A((x-2)^2+B(x-2)+C=8x+6$

$latex A(x^2-4x+4)+Bx-2B+C=8x+6$

$latex Ax^2-4Ax+4A+Bx-2B+C=8x+6$

The resulting system of equations is:

$$\phantom{-4}A\phantom{+B}\phantom{+C;} = 0 \\ -4A+B\phantom{+C;} = 8 \\\phantom{-}4A-2B+C = 6\\$$

Therefore: $latex B = 8$

And we have $latex -16+C=6\Rightarrow C =22$

Then:

$$\frac{8x+6}{(x-2)^3}=\frac{A}{(x-2)}+\frac{B}{(x-2)^2}+\frac{C}{(x-2)^3}$$

$$=\frac{0}{(x-2)}+\frac{8}{(x-2)^2}+\frac{22}{(x-2)^3}$$

Which leads to:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\int xdx+\int\frac{8x+6}{(x-2)^3}dx$$

$$=\int xdx+\int\frac{8}{(x-2)^2}dx+\int\frac{22}{(x-2)^3}dx$$

$$=\int xdx+8\int(x-2)^{-2}dx+22\int (x-2)^{-3}dx$$

$$=\frac{x^2}{2}-\frac{8}{x-2}-\frac{11}{(x-2)^2}+C$$

And the answer is:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\frac{x^2}{2}-\frac{8}{x-2}-\frac{11}{(x-2)^2}+C$$