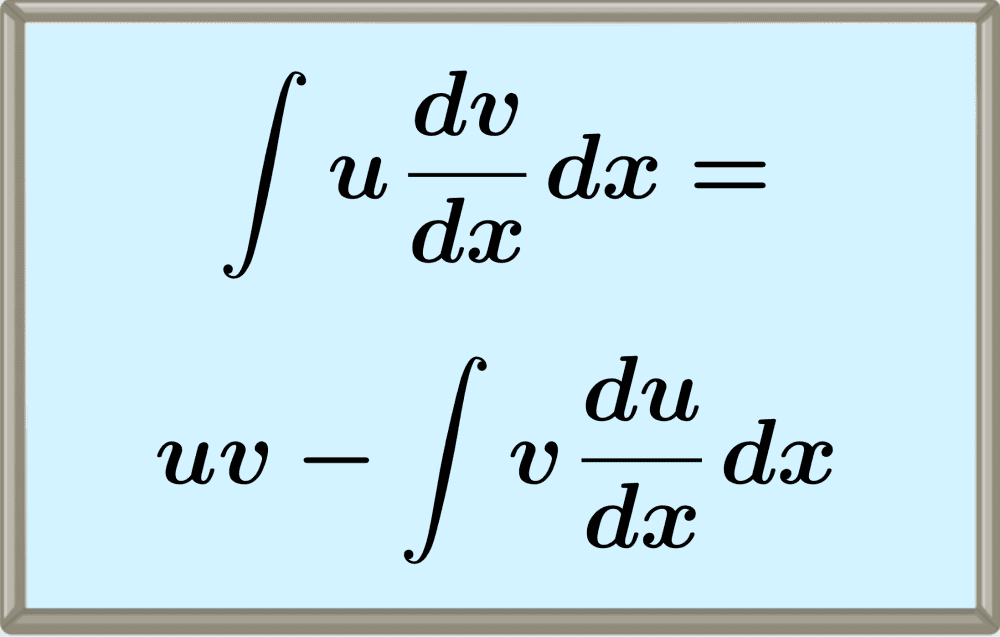Integration by parts allows us to “reduce” an integral to a simpler form, expressing it as the difference between two simpler integrals. This technique is especially useful when we want to evaluate integrals that cannot be easily found using other methods, such as substitution or trigonometric identities.
In this article, we will look at some solved integration by parts exercises. Then, we will see some practice problems to apply what we have learned.
How to integrate functions by parts
Integration by parts is used to integrate the product of two functions. To integrate functions using this method, we follow the steps below:
1. Choose two functions, u and dv/dx
The product of the two functions, $latex u\frac{dv}{dx}$ is the integrand.
2. Determine the derivative of u with respect to x and call it u′.
3. Determine the integral of dv/dx with respect to x and call it v
4. Use the formula for integration by parts:
$$\int u \frac{dv}{dx} dx=uv – \int v \frac{du}{dx}dx$$
or
$$\int u v^{\prime} dx=uv – \int v u^{\prime}dx$$
When using integration by parts, the choice of $latex u$ and $latex dv$ is not always obvious. However, there are some rules of thumb that can help guide your choice.
First, $latex u$ should be chosen such that it is an easy function to integrate, while $latex dv$ should be chosen such that it is an easy function to differentiate. This will make the integration and differentiation steps in the integration by parts formula simpler and easier to evaluate.
Second, it can sometimes be useful to choose $latex u$ and $latex dv$ so that the product $latex uv$ is as simple as possible. This can make the final step of the integration by parts formula easier to evaluate since you will be left with an integral that has a simple integrand.
Integration by parts – Examples with answers
EXAMPLE 1
Find the following integral:
$$\int x\cos x dx$$
Solution
To solve this integral, in which the product of two functions appears, the rule of integration by parts is used, according to which:
$$\int f(x)g'(x)dx=f(x)g(x)-\int g(x)f'(x)dx$$
If we specify the following:
- $latex f(x)=u$
- $latex g'(x)dx=dv\Rightarrow v=g(x)$
Then, the expression at the beginning is rewritten as follows:
$$\int udv=uv -\int vdu$$
Now, it only remains to select which of the functions is $latex v$ and which is $latex u$. For example, if you choose:
- $latex u =x$
- $latex du =dx$
- $latex dv =\cos x dx$
- $latex v =\int \cos x dx = \sin x$
Then:
$$\int x\cos x dx= x\sin x-\int \sin xdx =x\sin x+\cos x + C $$
$$\int x\cos x dx=x\sin x+\cos x + C $$
In general, it is advisable to take $latex dv$ as the part of the integrand that is most easily integrated, and $latex u$ as the one that is easiest to derive. The practice facilitates the decision, having as a goal that $latex vdu$ is easy to compute.
EXAMPLE 2
Calculate the integral:
$$\int xe^x dx$$
Solution
Selecting:
- $latex u =x$
- $latex du =dx$
- $latex dv =e^x dx$
- $latex v =\int e^x dx = e^x$
With the formula:
$$\int udv=uv -\int vdu$$
We have:
$$\int xe^x dx=xe^x-\int e^xdx$$
$$=xe^x-e^x+C$$
This result can be factored and we get:
$$\int xe^x dx=e^x(x-1)+C$$
EXAMPLE 3
Solve the following:
$$\int x \sqrt{x-1}dx$$
Solution
In this case, we specify:
- $latex u =x$
- $latex du =dx$
- $latex dv = \sqrt{x-1}\:dx$
- $latex v =\int \sqrt{x-1}\:dx =\dfrac{2}{3} (x-1)^\frac{3}{2}$
Using the formula:
$$\int udv=uv -\int vdu$$
We get:
$$\int x \sqrt{x-1}dx=x\cdot\dfrac{2}{3} (x-1)^\frac{3}{2}-\int \dfrac{2}{3} (x-1)^\frac{3}{2}dx$$
The integral obtained in the last step is now solved:
$$\int \dfrac{2}{3} (x-1)^\frac{3}{2}dx=\dfrac{2}{3}\int (x-1)^\frac{3}{2}dx$$
By means of a simple variable change:
- $latex dw=dx$
- $latex w=x-1$
We have:
$$\int (x-1)^\frac{3}{2}dx=\int w^\frac{3}{2}dw=\left[\dfrac{w^{\frac{3}{2}+1}}{\frac{3}{2}+1}\right]$$
$$=\dfrac{2}{5}w^{\frac{5}{2}}+C=\dfrac{2}{5}(x-1)^{\frac{5}{2}}+C$$
Finally, this result is substituted here:
$$\int x \sqrt{x-1}dx=x\cdot\dfrac{2}{3} (x-1)^\frac{3}{2}-\dfrac{2}{3}\int (x-1)^\frac{2}{3}dx$$
$$=\dfrac{2x}{3} (x-1)^\frac{3}{2}-\dfrac{2}{3}\cdot\dfrac{2}{5}(x-1)^{\frac{5}{2}}+C$$
$$=\dfrac{2x}{3} (x-1)^\frac{3}{2}-\dfrac{4}{15}(x-1)^{\frac{5}{2}}+C$$
$$=2 (x-1)^\frac{3}{2}\left[\dfrac{x}{3} -\dfrac{2}{15}(x-1)\right]+C$$
$$=2 (x-1)^\frac{3}{2}\left[\dfrac{x}{3} -\dfrac{2x}{15}+\dfrac{1}{15}\right]+C$$
$$=2 (x-1)^\frac{3}{2}\left[\dfrac{3x}{15} +\dfrac{2}{15}\right]+C$$
$$=\frac{2}{15}(x-1)^\frac{3}{2}\left(3x +2\right)+C$$
Then, the integral sought is:
$$\int x \sqrt{x-1}dx=\frac{2}{15}(x-1)^\frac{3}{2}\left(3x +2\right)+C$$
It is left as an exercise for the reader to verify that by deriving this result using the product rule for derivatives, and doing a little algebra, we obtain $latex x \sqrt{x-1}$$.
EXAMPLE 4
Find the following indefinite integral:
$$\int e^{x}\sin x dx$$
Solution
- $latex u=e^{x}$
- $latex du=e^{x}dx$
- $latex dv=\sin x dx$
- $latex v=-\cos x$
Following the formula for integration by parts $latex \int udv=uv -\int vdu$, it follows:
$$\int e^{x}\sin x dx=-e^{x}\cos x-\int -e^{x}\cos x\, dx$$
$$=-e^{x}\cos x+\int e^{x}\cos x\, dx$$
For this new integral, the technique of integration by parts is applied again, with this choice for $latex u$ and $latex dv$:
- $latex u=e^{x}$
- $latex du=e^{x}dx$
- $latex dv=\cos x dx$
- $latex v=\sin x$
Therefore:
$$\int e^{x}\cos x\, dx=e^{x}\sin x-\int e^{x}\sin x\,dx$$
This result is substituted in the integral previously mentioned:
$$\int e^{x}\sin x dx=-e^{x}\cos x+\int e^{x}\cos x\, dx$$
$$\int e^{x}\sin x dx+\int e^{x}\sin x\,dx=-e^{x}\cos x+e^{x}\sin x$$
$$2\int e^{x}\sin x dx=e^{x}(\sin x-\cos x+)+C$$
$$\int e^{x}\sin x dx=\frac{e^{x}(\sin x-\cos x+)}{2}+C$$
EXAMPLE 5
Solve the following:
$$\int x\sec ^2xdx$$
Solution
- $latex u=x$
- $latex du=dx$
- $latex dv=sec ^2xdx$
- $latex v=\tan x$
Using $latex \int udv=uv -\int vdu$, we have:
$$\int x\sec ^2xdx=x\tan x-\int\tan xdx$$
$$=x\tan x-\ln(\cos x)+C$$
EXAMPLE 6
What is the result of the following?
$$\int lnx\,dx$$
Solution
- $latex u=ln\,x$
- $latex du=\dfrac{dx}{x}$
- $latex dv=dx$
- $latex v=x$
Using $latex \int udv=uv -\int vdu$, we get:
$$\int lnx\,dx=xln\,x-\int x\left(\dfrac{dx}{x}\right)$$
$$=xln\,x-\int dx$$
$$\int lnx\,dx=xln\,x-x=x(ln\,x-1)$$
EXAMPLE 7
Find the following integral
$$\int x^2 lnx\;dx$$
Solution
The first step is to determine the values of $latex u$ and $latex v$:
- $latex u=lnx$
- $latex du=\dfrac{dx}{x}$
- $latex dv=\int x^2\;dx$
- $latex v=\dfrac{x^3}{3}$
Now, we apply the formula: $latex \int udv=uv -\int vdu$
And we get:
$$\int x^2 lnx\;dx=lnx\left(\frac{x^3}{3}\right)-\int \left(\frac{x^3}{3}\right)\left(\frac{dx}{x}\right)$$
$$=\frac{x^3lnx}{3}-\frac{1}{3}\int x^2dx=\frac{x^3lnx}{3}-\frac{x^3}{9}+C$$
$$=\frac{x^3}{3}\left(lnx-\frac{1}{3}\right)+C=\frac{x^3}{9}\left(3lnx-1\right)+C$$
Therefore:
$$\int x^2 lnx\;dx=\frac{x^3}{9}\left(3lnx-1\right)+C$$
EXAMPLE 8
Solve the following:
$$\int x\sin\, x\cos x \,dx$$
Solution
The following trigonometric identity is substituted in the integral:
$latex \sin 2x=2\sin x\cos x$
And we get:
$$\int x\sin\, x\cos x \,dx=\dfrac{1}{2}\int x\sin 2x\,dx$$
We specify the following:
- $latex u =x$
- $latex du =dv$
- $latex dv=\sin 2x\,dx$
- $latex v=-\dfrac{cos\,2x}{2}$
According to the formula for integration by parts: $latex \int udv=uv -\int vdu$
We get:
$$\int x\sin\, x\cos x \,dx=\dfrac{1}{2}\int x\sin 2x\,dx$$
$$=-\dfrac{xcos\,2x}{4}-\int-\dfrac{cos\,2x}{4}dx$$
$$=-\dfrac{xcos\,2x}{4}+\dfrac{1}{4}\int\cos\,2x\,dx$$
The integral obtained in the previous step is immediate:
$$\int\cos\,2x\,dx=\dfrac{1}{2}\sin\,2x+C$$
And by substituting, we obtain:
$$\int x\sin\, x\cos x \,dx=-\dfrac{xcos\,2x}{4}+\dfrac{1}{8}\sin\,2x+C$$
EXAMPLE 9
Find the following indefinite integral:
$$\int x (2x+5)^{10} dx$$
Solution
- $latex u=x$
- $latex du=dx$
- $latex dv=\int (2x+5)^{10}dx$
- $latex v=\dfrac{1}{22}(2x+5)^{11}$
Following the formula for integration by parts $latex \int udv=uv -\int vdu$, it results:
$$\int x (2x+5)^{10} dx=\dfrac{x}{22}(2x+5)^{11}-\int\dfrac{1}{22}(2x+5)^{11}dx$$
The new integral is solved with a simple change of variable, by specifying:
- $latex t = 2x+5$
- $latex dt = 2dx$
Then:
$$\int\dfrac{1}{22}(2x+5)^{11}dx=\dfrac{1}{44}\int t^{11}dt$$
$$=\frac{t^{12}}{528}+C$$
Substituting back, we obtain:
$$\int x (2x+5)^{10} dx=\dfrac{x}{22}(2x+5)^{11}-\frac{(2x+5)^{12}}{528}+C$$
The result can be factored:
$$\int x (2x+5)^{10} dx=\dfrac{x}{22}(2x+5)^{11}\left(1-\frac{2x+5}{24}\right)+C$$
$$\int x (2x+5)^{10} dx=\dfrac{x}{528}(2x+5)^{11}\left({19-2x}\right)+C$$
EXAMPLE 10
Solve the following:
$$\int x^3\sqrt{4-x^2}dx$$
Solution
To solve this integral, two methods of integration are applied. First, $latex v$ is determined by substitution, and then the integration by parts formula is applied:
- $latex u=x^2$
- $latex du=2xdx$
- $latex dv=x\sqrt{4-x^2}dx$
- $latex v=\int x\sqrt{4-x^2}dx=\int x({4-x^2})^\frac{1}{2}dx$
- $latex v=-\dfrac{1}{2}\int t^\frac{1}{2}dt=-\dfrac{1}{2}\left[\dfrac{ t^\frac{3}{2}}{\frac{3}{2}}\right]=-\dfrac{1}{3}(4-x^2)^\frac{3}{2}$
Integration by parts is now applied:
$$ \int udv=uv -\int vdu=-\dfrac{x^2}{3}(4-x^2)^\frac{3}{2}-\int-\dfrac{2x}{3}(4-x^2)^\frac{3}{2}dx$$
$$ =-\dfrac{x^2}{3}(4-x^2)^\frac{3}{2}+\dfrac{2}{3}\int x(4-x^2)^\frac{3}{2}dx$$
The new integral is solved by the same substitution used previously:
$$ \int x(4-x^2)^\frac{3}{2}dx=-\dfrac{1}{2}\int t^\frac{3}{2}dt=-\dfrac{1}{2}\left[\dfrac{ t^\frac{5}{2}}{\frac{5}{2}}\right]$$
$$=-\dfrac{1}{5}(4-x^2)^\frac{5}{2}$$
This result is substituted immediately:
$$ \dfrac{2}{3}\int x(4-x^2)^\frac{3}{2}dx=\dfrac{2}{3}\cdot\left(-\dfrac{1}{5}\right)(4-x^2)^\frac{5}{2}+C$$
$$ =-\dfrac{2}{15}(4-x^2)^\frac{5}{2}+C$$
With this, the requested integral can be solved:
$$\int x^3\sqrt{4-x^2}dx=-\dfrac{x^2}{3}(4-x^2)^\frac{3}{2}-\dfrac{2}{15}(4-x^2)^\frac{5}{2}+C$$
Integration by parts – Practice problems
See also
Interested in learning more about integrals? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
