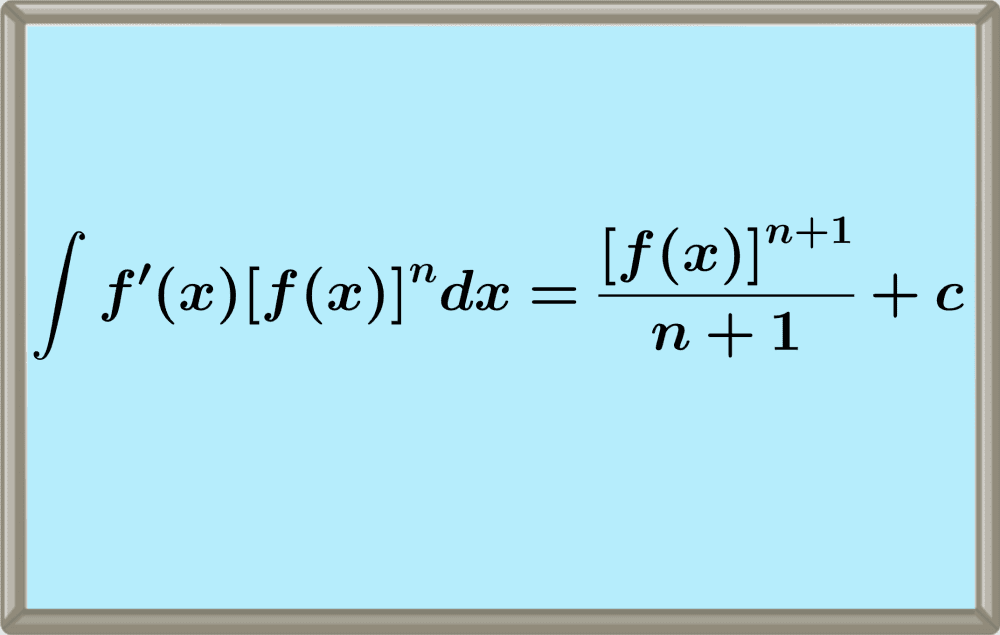The chain rule for integrals is an integration rule related to the chain rule for derivatives. This rule is used for integrating functions of the form f'(x)[f(x)]n.
Here, we will learn how to find integrals of functions using the chain rule for integrals. Then we will look at some examples where we will apply this rule.
Formula for the chain of integration
The formula for the chain rule of integrals is as follows:
$$\int f'(x)[f(x)]^ndx=\frac{[f(x)]^{n+1}}{n+1}+c$$
We can understand this formula by considering the function $latex f(x)=(x^2+1)^4$. Using the chain rule of derivatives, we find that its derivative is:
$latex f'(x)=8x(x^2+1)^3$
This means that we can write as follows:
$$\int 8x(x^2+1)^3dx=(x^2+1)^4+c$$
Now, we can recognize that the integrand $latex 8x(x^2+1)^3$ is of the form $latex f'(x)[f(x)]^n$.
In this example we have $latex f(x)=x^2+1$, $latex f'(x)=2x$ and $latex n=3$.
To look at another example, let’s consider the integral $latex \int x(3x^2-2)^5dx$. In this case, we observe that the derivative of $latex (3x^2-2)$ is $latex 6x$. Moreover, we have the term $latex x$ outside the main function $latex (3x^2-2)^5$.
This means that we consider $latex (3x^2-2)^6$, which when differentiated gives us $latex 36x(3x^2-2)^5$. Then, we have:
$$\int x(3x^2-2)^5=\frac{1}{36}(3x^2-2)^6+c$$
Solved exercises of the chain rule of integrals
EXAMPLE 1
Find the following integral:
$$\int (x-2)^2dx$$
Solution
To find the integral $latex \int (x-2)^2dx$, we can consider the function $latex f(x)=(x-2)^3$, which when derived gives us $latex f'(x)=3(x-2)^2$.
This means that the integral of $latex (x-2)^2$ is equal to:
$$\int (x-2)^2dx=\frac{(x-2)^3}{3}+c$$
EXAMPLE 2
Solve the following integral:
$$\int x(3x^2+6)^4dx$$
Solution
We can observe that the derivative of $latex 3x^2+6$ is $latex 6x$ and we have the term $latex x$ outside the main function $latex (3x^2+6)^4$.
This means we can consider that the derivative of $latex (3x^2+6)^5$ is $latex 30x(3x^2+6)^4$.
Then, we have the following integral:
$$\int x(3x^2+6)^4dx=\frac{(3x^2+6)^5}{30}+c$$
EXAMPLE 3
Find the following integral:
$$\int 4x^2(x^3-3)^5dx$$
Solution
To solve this integral, we observe that the derivative of $latex x^3-3$ is $latex 3x^2$.
Moreover, we have a term $latex x^2$ outside the main function $latex (x^3-3)^5$.
Then, we consider that the derivative of $latex (x^3-3)^6$ is $latex 18x^2(x^3-3)^5$. Thus, we have:
$$\int 4x^2(x^3-3)^5dx=\frac{4}{18}(x^3-3)^6+c$$
$$=\frac{2}{9}(x^3-3)^6+c$$
EXAMPLE 4
What is the result of the following integral?
$$\int (x+2)(x^2+4x-1)^3dx $$
Solution
We begin by noting that the derivative of $latex x^2+4x-1$ is $latex 2x+4=2(x+2)$.
Also, we see that we have the term $latex (x+2)$ outside the main function.
Then, considering that the derivative of $latex (x^2+4x-1)^4$ is
$$ 4(2x+4)(x^2+4x-1)^3=8(x+2)(x^2+4x-1)^3$$
Therefore, we have:
$$ \int (x+2)(x^2+4x-1)^3dx=\frac{1}{8}(x^2+4x-1)^4+c $$$$ =\frac{x(x^2-4)}{x^2-25} $$
EXAMPLE 5
Find the following integral:
$$ \int \frac{4x}{(3-x^2)^2}dx$$
Solution
In this case, we can start by writing the expression as follows to facilitate its resolution:
$$ \int \frac{4x}{(3-x^2)^2}dx=\int 4x (3-x^2)^{-2}$$
Now, we can observe that the derivative of $latex 3-x^2$ is $latex -2x$. Also, we have a term $latex x$ outside the main function.
Then, we consider that the derivative of $latex (3-x^2)^{-1}$ is $latex 2x(3-x^2)^{-2}$.
This means that this integral is solved as follows:
$$ \int \frac{4x}{(3-x^2)^2}dx=\frac{4}{2}(3-x^2)^{-1}+c $$
$$ =\frac{2}{3-x^2}+c $$
EXAMPLE 6
What is the result of the following integral?
$$ \int \frac{x}{\sqrt{x^2+3}}dx$$
Solution
We write the expression as follows:
$$ \int \frac{x}{\sqrt{x^2+3}}dx=\int x (x^2+3)^{-\frac{1}{2}}$$
Now, we see that the derivative of $latex x^2+3$ is $latex 2x$ and we have a term $latex x$ outside the main function.
Then, we can solve this by considering that the derivative of $latex (x^2+3)^{-{frac{1}{2}}}$ is:
$$2x\times \frac{1}{2} (x^2+3)^{-\frac{1}{2}}=x(x^2+3)^{-\frac{1}{2}}$$
This means that this integral is solved as follows:
$$ \int \frac{x}{\sqrt{x^2+3}}dx=(x^2+3)^{\frac{1}{2}}+c $$
$$ =\sqrt{x^2+3}+c $$
Chain rule for integration – Practice problems
By solving the following integral, the result can be expressed as a fraction. What is the numerator? $$\int \frac{25x^4}{(3-x^5)^2}dx$$
Write the numerator in the input box.
See also
Interested in learning more about integrals? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
