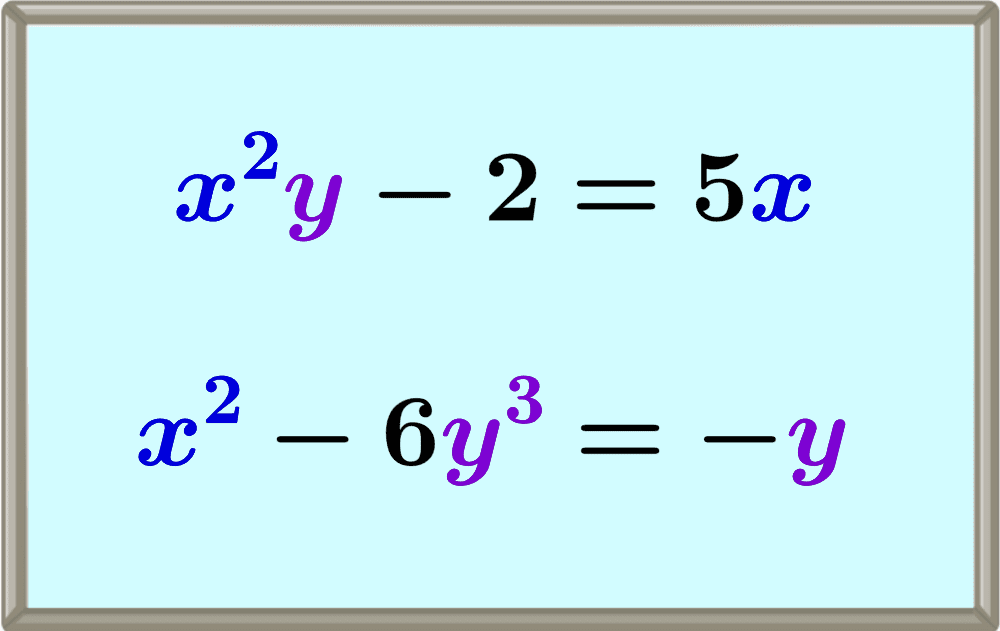Implicit Differentiation – Examples with Answers

Deriving on both sides of the equation:

$$ (x^2+y^2)^{\prime}=(16)^{\prime}$$

$$ (x^2)^{\prime}+(y^2)^{\prime} =(16)^{\prime}$$

Since the derivative of a constant is 0, we have:

$$ 2x+2yy^{\prime} =0$$

Then:

$$ 2x+2yy^{\prime} =0$$

Given that: $latex y^{\prime} =\dfrac{dy}{dx} $, then:

$$ 2x+2y\dfrac{dy}{dx} =0$$

When we isolate the derivative, we obtain:

$$\dfrac{dy}{dx} =-\dfrac{x}{y}$$

We start by deriving each term with respect to $latex x$:

$$\frac{d}{dx}(x^2y)=\frac{d}{dx}(4x)+\frac{d}{dx}(3)$$

The term $latex x^2y$ can be derived with respect to $latex x$ using the product rule. Then, we have:

$$x^2\frac{dy}{dx}+y(2x)=4+0$$

When we rearrange the equation for $latex \frac{dy}{dx}$, we have:

$$x^2\frac{dy}{dx}=4-2xy$$

$$\frac{dy}{dx}=\frac{4-2xy}{x^2}$$

Deriving each term with respect to $latex x$, we have:

$$\frac{d}{dx}(x+y)^4-\frac{d}{dx}(6x^2)=0$$

We can derive the term $latex (x+y)^4$ using the chain rule:

$$4(x+y)^3\left(1+\frac{dy}{dx}\right)-12x=0$$

The solved expression for $latex \frac{dy}{dx}$ is:

$$1+\frac{dy}{dx}=\frac{12x}{4(x+y)^3}$$

$$\frac{dy}{dx}=\frac{12x}{4(x+y)^3}-1$$

The first step is to state the first derivative on both sides of the equality:

$$\left[\ln(x+y)\right]^{\prime}=x^{\prime}$$

Immediately, the rules of derivation are applied, without forgetting the internal derivative in the argument of the natural logarithm:

$$\frac{(x+y)^{\prime}}{x+y}=1$$

$$\frac{1+y^{\prime}}{x+y}=1$$

$$1+y^{\prime}=x+y$$

The final step is to isolate $latex y^{\prime}$:

$$y^{\prime}=x+y-1$$

Following the procedure of the previous example, we start by deriving each side of the equation:

$$(3x^2y+4x)^{\prime}=(2y^3-7x^4)^{\prime}$$

$$ (3x^2y)^{\prime}+(4x)^{\prime}=(2y^3)^{\prime}-(7x^4)^{\prime}$$

Then the rules of the product and of the powers of derivatives are applied:

$$ 6xy +3x^2y^{\prime}+4=6y^2y^{\prime}-28x^3$$

Now, the terms containing $latex y^{\prime}$ are grouped together:

$$ 3x^2y^{\prime}-6y^2y^{\prime}=-28x^3-6xy-4 $$

We take out the common factor $latex y^{\prime}$:

$$ y^{\prime}(3x^2-6y^2)=-28x^3-6xy-4 $$

And rearranging:

$$ y^{\prime}=\dfrac{-28x^3-6xy-4}{3x^2-6y^2} $$

Given that $latex y^{\prime}=\dfrac{dy}{dx} $, it follows:

$$\dfrac{dy}{dx} =\dfrac{-28x^3-6xy-4}{(3x^2-6y^2)(3x^2-6y^2)} $$

$$\dfrac{dy}{dx} =-\left(\dfrac{2}{9}\right) \dfrac{14x^3+3xy+2}{(x^2-2y^2)^2}$$

The first step is to find $latex \frac{dy}{dx}$, for which it is convenient to derive implicitly:

$$ (x^3+y^3)^{\prime}=(9)^{\prime}$$

$$ 3x^2+3y^2y^{\prime}=0$$

Therefore:

$$ y^{\prime}=-\frac{x^2}{y^2}$$

The slope $latex m$ of the tangent straight line to the curve at $latex (1,2)$ is obtained by evaluating $latex y^{\prime}$ at that point:

$$m=-\left.\frac{x^{2}}{y^2} \right|_{x_o=1,y_o=2}=-\frac{1}{4}$$

Once the slope is obtained, the equation of the tangent line is:

$$y-y_o=m(x-x_o)$$

$$y-2=-\frac{1}{4}(x-1)$$

$$y=-\frac{x}{4}+\frac{9}{4}$$

$$4y=9-x$$

We determine $latex \dfrac{dy}{dx}$ by implicit differentiation:

$$\left[\frac{x^2}{16}-\frac{y^2}{9}\right]^{\prime}=(1)^{\prime}$$

$$\frac{x}{8}-\frac{2yy^{\prime}}{9}=0$$

$$y^{\prime}=\frac{9x}{16y}$$

The slope $latex m$ of the tangent straight line to the curve at the indicated point is obtained by evaluating $latex y^{\prime}$ at the coordinates $latex \left(-5,\dfrac{9}{4}\right)$:

$$m=-\left.\frac{9x}{16y} \right|_{x_o=-5,y_o=\frac{9}{4}}=\dfrac{9(-5)}{16\left(\dfrac{9}{4}\right)}=-\dfrac{5}{4}$$

The equation of the tangent line we are looking for is:

$$y-y_o=m(x-x_o)$$

In which the values $latex m =-\dfrac{5}{4}$, $latex x_o=-5$ and $latex y_o=\dfrac{9}{4}$ are substituted:

$$y-\frac{9}{4}=-\frac{5}{4}\left[x-(-5)\right]$$

$$4y-9=-20x-25$$

$$4y=-20x-16$$

And the line we are looking for is:

$$y=-5x-4$$

Differentiating both sides of the equation:

$$ x^{\prime} = \left[\sec\left(\frac{1}{y}\right)\right]^{\prime}$$

Knowing that $latex(\sec u)´=\sec u\tan u u´$, we have:

$$ 1 = \sec\left(\frac{1}{y}\right)\tan \left(\frac{1}{y}\right)(-1)y^{-2}y^{\prime} $$

Finally, we isolate $latex y^{\prime}$:

$$y^{\prime}=-\frac{y^2}{\sec\left(\dfrac{1}{y}\right)\tan \left(\dfrac{1}{y}\right)}$$

In this function there are square roots, so it is convenient to write them as fractional exponents, to make the calculation easier:

$$\sqrt {xy}+2x=\sqrt{y}$$

$$(xy)^\frac{1}{2}+2x=(y)^\frac{1}{2}$$

$$x^\frac{1}{2}y^\frac{1}{2}+2x=y^\frac{1}{2}$$

Then the rules of derivation are applied to both sides of the equality:

$$[x^\frac{1}{2}y^\frac{1}{2}+2x]^{\prime}=[(y)^\frac{1}{2}]^{\prime}=$$

$$\left(\frac{1}{2}\right)x^{-\frac{1}{2}}y+x^\frac{1}{2}\left(\frac{1}{2}\right)y^{-\frac{1}{2}}y^{\prime}+2=\left(\frac{1}{2}\right)(y)^{-\frac{1}{2}}y^{\prime}$$

The next step is to group the terms that contain $latex y^{\prime}$ to the left of the equality and multiply everything by $latex 2$ to eliminate denominators:

$$x^\frac{1}{2}y^{-\frac{1}{2}}y^{\prime}-y^{-\frac{1}{2}}y^{\prime}=-4-x^{-\frac{1}{2}}y$$

We factor $latex y^{\prime}$:

$${y^{-\frac{1}{2}}y^{\prime}}\left(x^\frac{1}{2}-1\right)={-4-x^{-\frac{1}{2}}y}$$

Before solving, the equation is rewritten again using roots:

$$y^{\prime}\left(\frac{\sqrt x-1}{\sqrt y}\right)=-4-\frac{y}{\sqrt x}=\frac{-4\sqrt x-y}{\sqrt x}$$

By isolating $latex y^{\prime}$, we have:

$$y^{\prime}=-\frac{(4\sqrt x+y)\sqrt y}{\sqrt x(\sqrt x-1)}$$

$$y^{\prime}=\frac{4\sqrt {xy}+y\sqrt y}{x-\sqrt x}$$

Differentiating both sides of the equation:

$$\left[e^{2x+3y}\right]^{\prime}=\left[x^2-\ln (xy^3)\right]^{\prime}$$

$$e^{2x+3y}(2+3y^{\prime})=2x-\frac{1}{xy^3}(y^3+3xy^2y^{\prime})$$

$$2e^{2x+3y}+3y^{\prime}e^{2x+3y}=2x-\frac{1}{x}-\frac{3y^{\prime}}{y}$$

Next, we group the terms containing $latex y^{\prime}$ to the left of the equality:

$$3y^{\prime}e^{2x+3y}+3y^{\prime}y^{-1}=2x-x^{-1}-2e^{2x+3y}$$

We factor out $latex y^{\prime}$:

$$3y^{\prime}\left(e^{2x+3y}+y^{-1}\right)=2x-x^{-1}-2e^{2x+3y}=$$

And finally, we solve for $latex y^{\prime}$:

$$y^{\prime}=\frac{2x-x^{-1}-2e^{2x+3y}}{3(e^{2x+3y}+y^{-1})}$$

We start by differentiating both sides of the equation:

$$\left[\cos(x^2+1)\right]^{\prime}=\left(xe^y\right)^{\prime}$$

Then we apply the derivation rules for the cosine on the left, whose argument is $latex x^2+1$, and the exponential on the right:

$$-2x\sin(x^2+1)=e^y+xe^yy^{\prime}$$

$$xe^yy^{\prime}=-2x\sin(x^2+1)-e^y$$

Then we isolate $latex y^{\prime}$:

$$y^{\prime}=\frac{-2x\sin(x^2+1)-e^y}{xe^y}$$

Since $latex y^{\prime} =\dfrac{dy}{dx} $, we have:

$$\dfrac{dy}{dx} =\frac{-2x\sin(x^2+1)-e^y}{xe^y}$$

First of all, the first derivative $latex y^{\prime}$ is posed:

$$(y^2)^{\prime}=(x^3)^{\prime}$$

$$2yy^{\prime}=3x^2$$

We isolate $latex y^{\prime}$:

$$y^{\prime}=\frac{3x^2}{2y}$$

$$y^{\prime}=\frac{3}{2}x^2y^{-1}$$

Now the second derivative $latex y^{\prime\prime}$ is posed:

$$y^{\prime \prime}=\left[\frac{3}{2}x^2y^{-1}\right]^{\prime}$$

The next step is to apply the derivative of a product to the right-hand side of the equation:

$$y^{\prime \prime}=\frac{3}{2}\left[2xy^{-1}+x^2(-1)y^{-2}y^{\prime}\right]$$

$$y^{\prime \prime}=\frac{3}{2}\left[2xy^{-1}-x^2y^{-2}y^{\prime}\right]$$

Next, we substitute the expression for $latex y^{\prime}$ that we obtained previously:

$$y^{\prime \prime}=\frac{3}{2}\left[2xy^{-1}-x^2y^{-2}\left(\frac{3}{2}x^2y^{-1}\right)\right]$$

And we get:

$$y^{\prime \prime}=\frac{3xy^{-1}}{4}\left(4-3x^3y^{-2}\right)$$