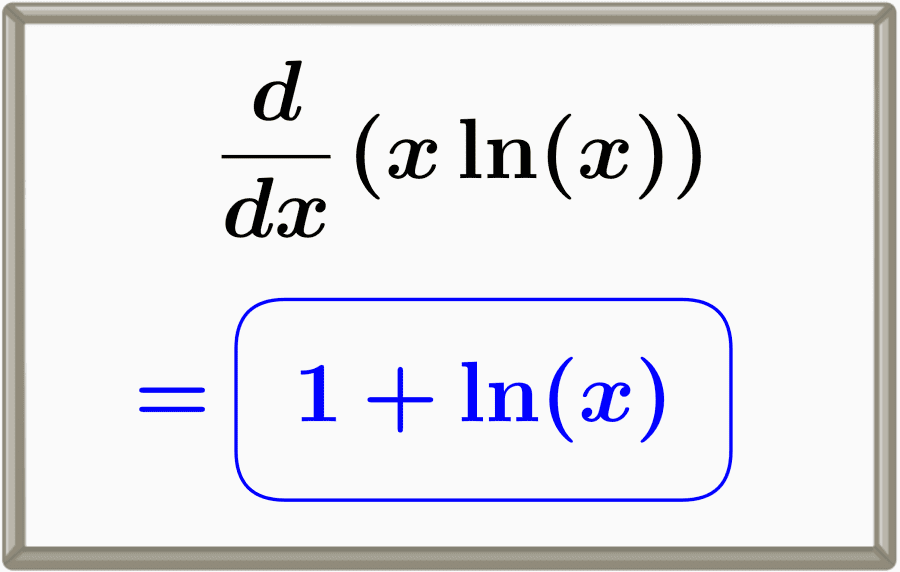The derivative of x ln(x) is equal to 1+ln(x). This derivative can be found using the product rule of derivatives.
In this article, we will learn how to obtain the derivative of x ln(x). We will review some principles, graphical comparisons x ln(x) and its derivative, and will explore the proofs of this derivative.
Proofs of the Derivative of Natural Logarithm, x ln(x)
Listed below are the proofs of the derivative of \(x\ln{(x)}\). These proofs can also serve as the main methods of deriving this function.
Proof of the derivative of x ln(x) using the Product Rule formula
In the derivative process of \(x\ln{(x)}\), the product rule is used since the natural log of x is being multiplied by another x. Here, we have two multiplicands. They are two functions being multiplied together that we cannot algebraically simplify.
You can review the product rule formula by looking at this article: Product Rule of derivatives. You can also look at this article for the proof of the natural logarithm’s derivative using limits: Derivative of Natural log (ln(x)).
Let’s have the derivative of the function
$$ f(x) = x\ln{(x)}$$
We can figure out the two functions being multiplied. There is a natural logarithmic function and a monomial in this case. Setting the first multiplicand/term as u, we have
$$ u = x$$
and setting the second multiplicand/term as v, we have
$$ v = \ln{(x)}$$
Recall that the derivative product formula is
$$ \frac{d}{dx} uv = u \frac{d}{dx} v + v \frac{d}{dx} u$$
That is, the function u times v is derived by multiplying u by the derivative of v and then added to v multiplied by the derivative of u. Applying this formula to our given function, we have
$$ \frac{d}{dx} uv = (x) \frac{d}{dx} (\ln{(x)}) + (\ln{(x)}) \frac{d}{dx} (x)$$
Evaluating the derivative of u by using power rule and v by using the derivative of natural logarithm, we have
$$ \frac{d}{dx} uv = (x) \cdot \left(\frac{1}{x} \right) + (\ln{(x)}) \cdot (1)$$
Simplifying, we have
$$ \frac{d}{dx} uv = \frac{x}{x} + (\ln{(x)}) $$
$$ \frac{d}{dx} uv = 1 + (\ln{(x)}) $$
As a result, we arrive at the \(x\ln{(x)}\) derivative formula.
$$ \frac{d}{dx} x\ln{(x)} = 1 + (\ln{(x)}) $$
Proof of the derivative of x ln(x) using implicit differentiation
You are advised to learn/review the derivatives of exponential functions and implicit differentiation for this proof.
Given that the equation
$$ y = x\ln{(x)}$$
Applying a logarithmic property
$$ y = \ln{(x)^x}$$
$$ y = \ln{\left(x^x\right)}$$
In general logarithmic form, it is
$$ \log_{e}{x^x} = y$$
And in exponential form, it is
$$ e^y = x^x$$
Implicitly deriving the exponential form in terms of x, we have
$$ e^y = x^x$$
$$ e^y \cdot \frac{d}{dx} = \frac{d}{dx} (x^x) $$
$$ e^y \cdot \frac{d}{dx} = \frac{d}{dx} (x^x + x^x \ln{(x)}) $$
Isolating \( \frac{dy}{dx} \), we have
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{e^y} $$
We recall that in the beginning, \( y = x\ln{(x)} \) or \( y = \ln{\left(x^x\right)} \). Substituting this to the y of our derivative, we have
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{e^{\left(\ln{\left(x^x\right)}\right)}} $$
Simplifying and applying a property of logarithm, we have
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{x^x} $$
$$ \frac{dy}{dx} = \frac{x^x}{x^x} + \frac{x^x \ln{(x)}}{x^x} $$
$$ \frac{dy}{dx} = 1 + \ln{(x)} $$
Evaluating, we now have the derivative of \( y = x\ln{(x)} \)
$$ y’ = 1 + \ln{(x)} $$
Graph of x ln(x) vs. its derivative
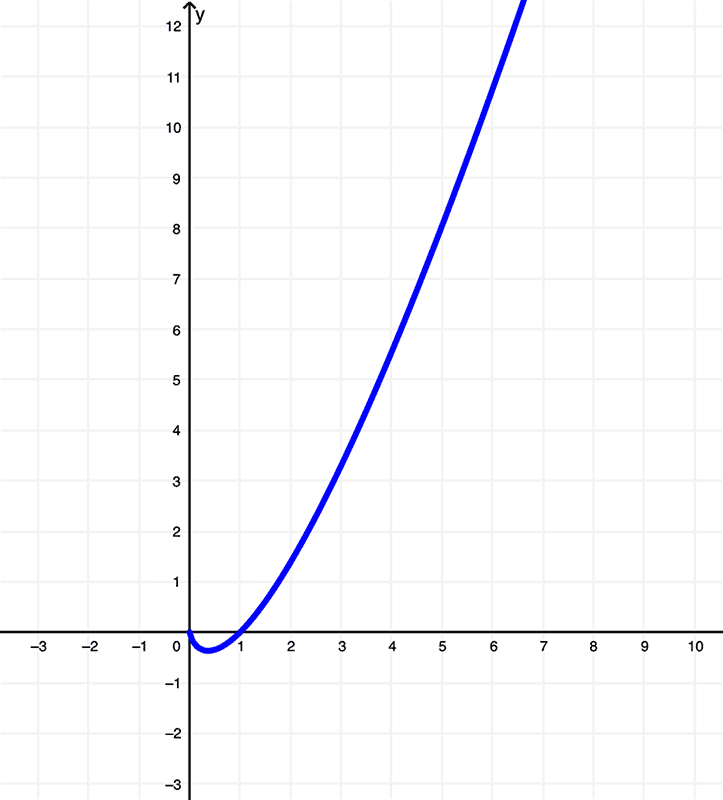
We have the function
$$ f(x) = x\ln{(x)}$$
and its graph is
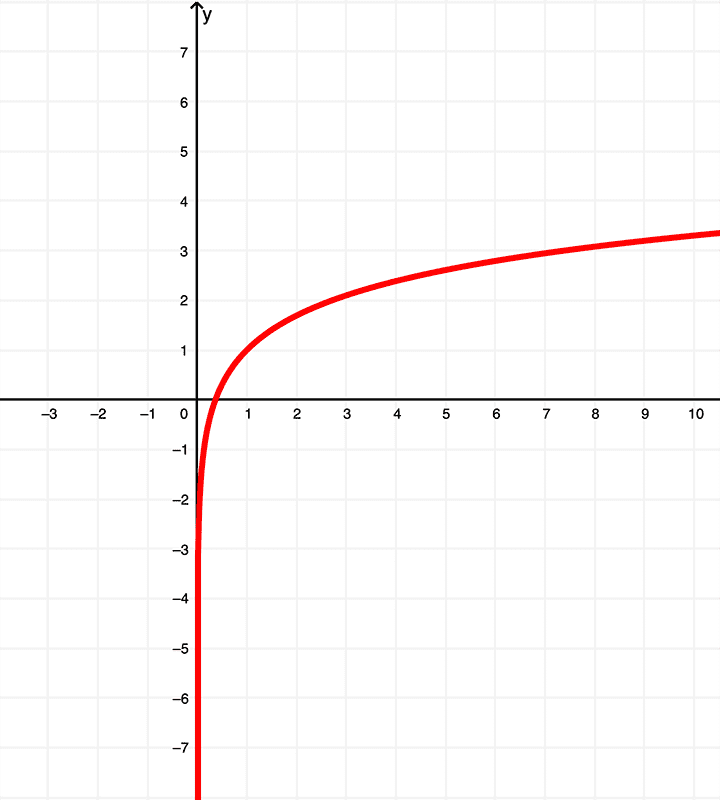
And as we learned above, deriving \(f(x) = x\ln{(x)}\) will be
$$ f'(x) = 1 + \ln{(x)}$$
which is illustrated graphically as
Illustrating both graphs in one, we have
By examining the differences between these functions using these graphs, you can see that the original function \(f(x) = x\ln{(x)}\) has a domain of
\( (0,\infty) \) or \( x | x > 0 \)
and lies within the range of
\( \left[-\frac{1}{e}, \infty \right) \) or \( y | y \geq -\frac{1}{e} \)
whereas the derivative \(f'(x) = 1 + \ln{(x)}\) has a domain of
\( (0,\infty) \) or \( x | x > 0 \)
which lies within the range of
\( (-\infty,\infty) \) or all real numbers
See also
Interested in learning more about the derivatives of logarithmic functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
