The natural logarithm, also denoted as ln(x), is the logarithm of x to base e (euler’s number). The derivative of the natural logarithm is equal to one over x, 1/x. We can prove this derivative using limits or implicit differentiation.
In this article, we will learn how to derive the natural logarithmic function. We will review some fundamentals, definitions, formulas, graphical comparisons of ln(x) and its derivative, proofs, and some examples.
Proofs of the Derivative of Natural Logarithm of x
Proof of the derivative of ln(x) using the first principle
Before learning the proof of the derivative of the natural logarithmic function, you are hereby recommended to learn/review the first principle of limits, Euler’s number, and L’hopital’s rule as prerequisites.
To review, any function can be derived by equating it to the limit of
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Suppose we are asked to get the derivative of
$$ f(x) = \ln{(x)}$$
we have
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \ln{(x+h)} – \ln{(x)} }{h}}$$
With this equation, it is still not possible to express the limit due to the denominator h where if zero is substituted, will be undefined. Therefore, we can check if applying some properties of logarithms can be useful.
The division property of logarithm states that the log of a quotient is the difference of the logs. We can observe that the numerator satisfies this condition. Applying this, we have
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \ln{(x+h)} – \ln{(x)} }{h}}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ \ln{\left(\frac{x+h}{x} \right)} }{h}}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \ln{\left(\frac{x+h}{x} \right)} \cdot \frac{1}{h}}$$
Rearranging, we have
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{1}{h} \cdot \ln{\left(\frac{x+h}{x} \right)} }$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{1}{h} \cdot \ln{\left(1 + \frac{h}{x} \right)} }$$
We can try to eliminate the denominator h by substituting
$$ h = vx $$
where
$$ v = \frac{h}{x} $$
which algebraically proves that as h approaches 0, v also approaches 0.
Substituting, we have
$$ \frac{d}{dx} f(x) = \lim \limits_{v \to 0} { \frac{1}{vx} \cdot \ln{\left(1 + v \right)} }$$
Re-arranging, we have
$$ \frac{d}{dx} f(x) = \lim \limits_{v \to 0} { \frac{1}{x} \cdot \frac{1}{v} \ln{\left(1 + v \right)} }$$
We may now evaluate the limit of \(\frac{1}{x}\) as v approaches 0
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{v} \ln{\left(1 + v \right)} }$$
By applying the power property of logarithms to our remaining limit, we have
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \left( \ln{\left(1 + v \right)} \right)^{\frac{1}{v}} }$$
As you realize, the natural log we have in the remaining limit now is exactly the mathematical definition of the Euler’s number e.
If
$$ (1 + v)^{\frac{1}{v}} = e $$
based on Euler’s number definition, then
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} {\ln{(e)}}$$
Evaluating ln(e), we know that it is equal to one. Hence, we have
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} {(1)}$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot (1)$$
Therefore, the derivative of the natural logarithm in the form of \(\ln{(x)}\) is:
$$ \frac{d}{dx} (\ln{(x)}) = \frac{1}{x}$$
Alternatively, instead of the Euler’s number definition, we may also evaluate the same remaining limit by applying the L’hopital’s rule.
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{v} \ln{\left(1 + v \right)} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{\ln{\left(1 + v \right)}}{v} }$$
This remaining limit satisfies the condition \(\frac{0}{0}\). Evaluating, we have
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{\ln{\left(1 + v \right)}}{v} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{ \frac{1}{1+v} }{1} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1+v} }$$
Evaluating by substituting the approaching value of v, we have
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1+(0)} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { 1 }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot (1)$$
$$ \frac{d}{dx} (\ln{(x)}) = \frac{1}{x}$$
Proof of the derivative of ln(x) using implicit differentiation
In this proof, you are hereby recommended to learn/review the derivatives of exponential functions and implicit differentiation.
Suppose we have the equation
$$ y = \ln{(x)}$$
In general logarithmic form, it is
$$ \log_{e}{x} = y$$
And in exponential form, it is
$$ e^y = x$$
Implicitly deriving the exponential form in terms of x, we have
$$ e^y = x$$
$$ \frac{d}{dx} (e^y) = \frac{d}{dx} (x) $$
$$ e^y \cdot \frac{dy}{dx} = 1 $$
Isolating \(\frac{dy}{dx}\), we have
$$ \frac{dy}{dx} = \frac{1}{e^y} $$
We recall that in the beginning, \(y = \ln{(x)}\). Substituting this to the y of our derivative, we have
$$ \frac{dy}{dx} = \frac{1}{e^{(\ln{(x)})}} $$
Evaluating, we now have the derivative of \(y = \ln{(x)}\)
$$ y’ = \frac{1}{x} $$
Graph of ln(x) x vs. its derivative
Given the function
$$ f(x) = \ln{(x)}$$
its graph is
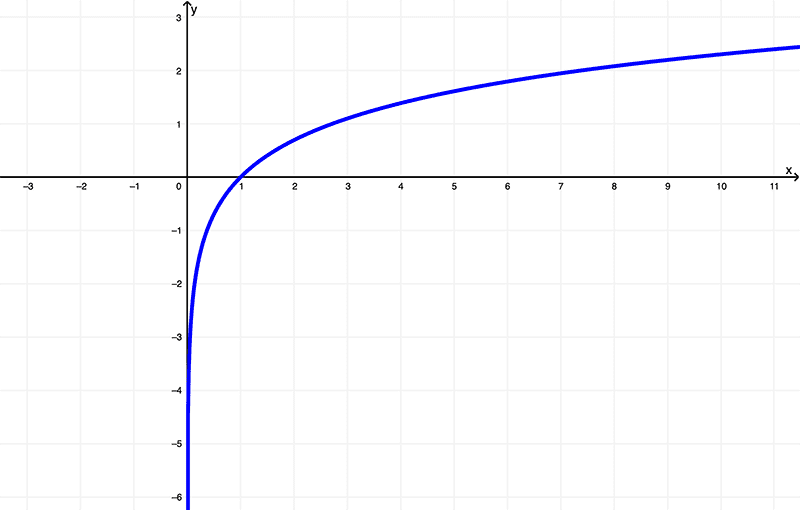
And as we know by now, by deriving \(f(x) = \ln{(x)}\), we get
$$ f'(x) = \frac{1}{x}$$
which is illustrated graphically as
Comparing both graphs in one, we have
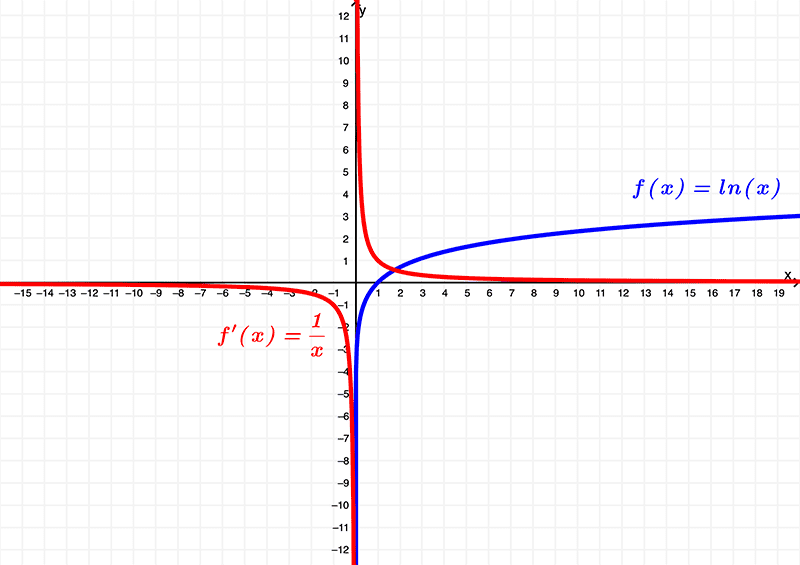
Using the graphs, it can be seen that the original function (f(x) = \ln{(x)}) has a domain of
\( (0,\infty) \) or \( x | x > 0 \)
and exists within the range of
\( (-\infty, \infty) \) or all real numbers
whereas the derivative \(f'(x) = \frac{1}{x}\) has a domain of
\( (-\infty,0) \cup (0,\infty) \) or \( x | x \neq 0 \)
and exists within the range of
\( (-\infty,0) \cup (0,\infty) \) or \( y | y \neq 0 \)
Examples
The following examples show how to derive a composite natural logarithm function.
EXAMPLE 1
Find the derivative of $latex f(x) = \ln(4x)$
Solution
This is a composite natural logarithm function, so we can use the chain rule to derive it.
Considering $latex u=4x$ as the inner function, we can write $latex f(u)=\ln(u)$. Then, using the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{u} \times 4$$
Substituting $latex u=4x$ back into the function, we have:
$$\frac{dy}{dx}=\frac{4}{4x}$$
EXAMPLE 2
Determine the derivative of $latex F(x) = \ln(4x^2-6x)$.
Solution
Let’s use the chain rule. Then, we consider $latex u=4x^2-6x$ as the inner function and $latex f(u)=\ln(u)$ as the outer function.
Therefore, we start by finding the derivative of the external function:
$$\frac{d}{du} ( \ln(u) ) = \frac{1}{u}$$
Now, we find the derivative of the inner function, $latex g(x)$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(4x^2-6x)$$
$$\frac{d}{dx}(g(x)) = 8x-6$$
We multiply the derivative of the inner function by the derivative of the outer function:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \frac{1}{u} \cdot 8x-6$$
Finally, we use the substitution $latex u=4x^2-6x$ and simplify:
$$\frac{dy}{dx} = \frac{1}{4x^2-6x} \cdot 8x-6$$
$$\frac{dy}{dx} = \frac{8x-6}{4x^2-6x}$$
$$\frac{dy}{dx} = \frac{4x-3}{2x^2-3x}$$
EXAMPLE 3
What is the derivative of $latex f(x) = \ln(\sin(x))$?
Solution
In this case, we consider $latex u=\sin(x)$ as the inner function. Therefore, $latex f(u)=\ln(u)$ is the outer function.
Using the chain rule, we can write:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{u} \times \cos(x)$$
Substituting $latex u=\sin(x)$ back into the function, we have:
$$\frac{dy}{dx}=\frac{1}{\sin(x)} \times \cos(x)$$
$$\frac{dy}{dx}=\frac{\cos(x)}{\sin(x)}$$
$$\frac{dy}{dx}=\cot(x)$$
Practice of derivatives of natural logarithm
See also
Interested in learning more about the derivatives of logarithmic functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
