Rate of change exercises are solved by finding the derivative of an equation with respect to the main variable. Generally, the chain rule is used to find the required rate of change.
Here, we will look at several examples with answers of the rate of change using derivatives. Then, we will look at some practice problems to apply what we have learned.
What is the rate of change in calculus?
The rate of change represents the relationship between changes in the dependent variable compared to changes in the independent variable.
The following derivative
$$\dfrac{dy}{dx}=\lim_{\delta \to 0} \frac{\delta y }{\delta x}$$
is the rate of change of $latex y$ with respect to $latex x$.
This rate of change shows how changes in $latex y$ are related to changes in $latex x$. For example, if $latex \dfrac{dy}{dx}=5$, then $latex y$ increases 5 times faster than $latex x$.
Frequently, other letters besides $latex x$ and $latex y$ are used. For example, in physics, it is common to use $latex s$ to indicate the position of an object. Then:
- $latex \dfrac{ds}{dt}$ is the velocity since it represents the rate of change of the displacement with respect to time.
- $latex \dfrac{d^2s}{dt^2}$ is the acceleration because it represents the rate of change of velocity with respect to time.
Many practical situations involve rates of change related to the use of the chain rule of derivatives, as shown in the following examples.
Examples with answers of rate of change with derivatives
EXAMPLE 1
The side of a square piece of metal increases at a rate of 0.1 cm per second when it is heated. What is the rate of change of the area of the metal?
Solution
To solve this problem, we have to start by finding an equation for the area of the square piece of metal.
If we represent the sides of the piece of metal with $latex x$, its area is $latex A=x^2$.
We have that the rate of change of the length of a side with respect to time, i.e., $latex \dfrac{dx}{dt}$, is 0.1 cm/s.
We want to find the rate of change of the area with respect to time, that is, $latex \dfrac{dA}{dt}$.
If we derive $latex A=x^2$, we have $latex \dfrac{dA}{dx}=2x$. Also, since $latex \dfrac{dx}{dt}=0.1$, we can use the chain rule:
$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$
$latex =2x \times 0.1$
$$\dfrac{dA}{dt}=0.2x$$
The rate of change of the area is $latex 0.2x$ cm2/s.
EXAMPLE 2
The side of a square is increasing at a rate of 5 cm/s. Find the rate of change of area when the length of one side is 10 cm.
Solution
Again, we start by finding an equation for the area of the square in terms of its sides.
If we represent the sides of the square with $latex x$, its area is $latex A=x^2$.
From the question, we know the rate of change of the length of a side with respect to time, that is, $latex \dfrac{dx}{dt}=$5 cm/s.
To find the rate of change of the area, that is, $latex \dfrac{dA}{dt}$, we derive $latex A=x^2$ and use the chain rule:
$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$
$latex =2x \times 5$
$$\dfrac{dA}{dt}=10x$$
When the length of a side is 10 cm, the rate of change of the area of the square is $latex 10(10)=100$ cm2/s.
EXAMPLE 3
The radius of a circle is increasing at a rate of $latex{1}{3}$ cm/s. Find the rate of change of the area when the radius is 5 cm.
Solution
In this case, we have a circle. The equation of the area with respect to the radius of the circle is $latex A=\pi r^2$.
If we differentiate $latex A=2 \pi r^2$ with respect to the radius, we have $latex \dfrac{dA}{dr}=2 \pi r$.
Now, from the question, we know that the rate of change of the radius of the circle with respect to time, that is, $latex \dfrac{dr}{dt}$, is $latex \frac{1}{3}$ cm/s.
Then, to find the rate of change of the area with respect to time, that is, $latex \dfrac{dA}{dt}$, we can use the chain rule:
$$\dfrac{dA}{dt}=\dfrac{dA}{dr}\dfrac{dr}{dt}$$
$latex =2\pi r \times \frac{1}{3}$
$$\dfrac{dA}{dt}=\frac{2\pi r}{3}$$
When the radius is 5 cm, the rate of change of the area of the circle is $latex \frac{2\pi(5)}{3}=\frac{10\pi}{3}$ cm2/s.
EXAMPLE 4
The area of a square is increasing at the rate of 7 cm2/s. Find the rate of change of length of a side when the area is 100 cm2.
Solution
As we already know, the area of a square with respect to its sides can be represented by the equation $latex A=x^2$, where x is a side.
Now, solving for $latex x$, we have $latex x=\sqrt{A}$. When we derive, we have $latex \dfrac{dx}{dA}=\frac{1}{2\sqrt{A}}$.
In this case, we have that the rate of change of the area of the square with respect to time, that is, $latex \dfrac{dA}{dt}$, is 7 cm2/s.
Then, we find the rate of change of the length of a side with respect to time, i.e., $latex \dfrac{dx}{dt}$, using the chain rule:
$$\dfrac{dx}{dt}=\dfrac{dA}{dt}\dfrac{dx}{dA}$$
$$=7 \times \frac{1}{2\sqrt{A}}$$
$$\dfrac{dx}{dt}=\frac{7}{2\sqrt{A}}$$
When the area is 100 cm2, the rate of change of one side of the square is $latex \frac{7}{2\sqrt{100}}=\frac{7}{20}$ cm/s.
EXAMPLE 5
The area of a circle is increasing at the rate of (4π) cm2/s. Find the rate of change of the radius when this radius is $latex \frac{1}{2}$ cm.
Solution
We can represent the area of a circle with respect to the radius with the equation $latex A=\pi r^2$.
When we derive this equation with respect to $latex r$, we have $latex \dfrac{dA}{dr}=2 \pi r$.
We have that the rate of change of the area of the circle with respect to time, that is, $latex \dfrac{dA}{dt}$, is (4π) cm2/s.
Now, to find the rate of change of the radius with respect to time, that is, $latex \dfrac{dr}{dt}$, we use the chain rule:
$$\dfrac{dr}{dt}=\dfrac{dA}{dt}\dfrac{dr}{dA}$$
We note that $latex \dfrac{dr}{dA}$ is the reciprocal of $latex \dfrac{dA}{dr}$. Then, we have:
$$\dfrac{dr}{dt}=4\pi \times \dfrac{1}{2 \pi r}$$
$$\dfrac{dr}{dt}=\frac{2}{r}$$
When the radius is $latex \frac{1}{2}$ cm, the rate of change of the radius of the circle is $latex \frac{2}{\frac{1}{2}}=4$ cm/s.
EXAMPLE 6
The volume of a cube is increasing at the rate of 18 cm3/s. Find the rate of change of the length of one side when the volume is 125 cm3.
Solution
If we use $latex x$ to represent the sides of the cube, its volume is $latex V=x^3$.
Solving for $latex x$, we have $latex x=\sqrt[3]{V}$. Differentiating, we have $latex \dfrac{dx}{dV}=\frac{1}{3\sqrt[3]{V}}$.
Since the question tells us that the volume of the cube increases at a rate of 18 cm3/s, we have $latex \dfrac{dV}{dt}=18$ cm3/s.
Then, we find the rate of change of one side of the cube with respect to time, $latex \dfrac{dx}{dt}$, by applying the chain rule:
$$\dfrac{dx}{dt}=\dfrac{dV}{dt}\dfrac{dx}{dV}$$
$latex =18 \times \frac{1}{3\sqrt[3]{V}}$
$$\dfrac{dA}{dt}=\frac{18}{3\sqrt[3]{V}}$$
When the volume is 125 cm3, the rate of change of one side of the cube is $latex \frac{18}{3\sqrt[3]{125}}=\frac{6}{25}$ cm/s.
EXAMPLE 7
A completely spherical balloon is being inflated at a rate of 3 cm3/s. Find the rate of change of radius when the radius is 2 cm.
Solution
If we represent the radius by $latex r$ and the volume by $latex V$, we have $latex V= \frac{4}{3} \pi r^3$. Then, its derivative is:
$$\dfrac{dV}{dr}=4\pi r^2$$
From the question, we have $latex \dfrac{dV}{dt}=3$. Then, using the chain rule, we have:
$$\dfrac{dV}{dt}=\dfrac{dV}{dr}\dfrac{dr}{dt}$$
$$3=4\pi r^2 \times \dfrac{dr}{dt}$$
$$\dfrac{dr}{dt}=\frac{3}{4\pi r^2}$$
When $latex r=2$, we have:
$$\frac{dr}{dt}\Big|_{r=2}=\frac{3}{4\pi (2)^2}=\frac{3}{16\pi}$$
The rate of change of the radius when the radius is 2 cm is $latex \frac{3}{16\pi}$ cm/s.
EXAMPLE 8
The surface area of a sphere is increasing at the rate of 2 cm2/s. Find the rate of change of radius when the surface area is (100π) cm2.
Solution
When we represent the radius by $latex r$ and the surface area by $latex A_{s}$, we have $latex A_{s}=4\pi r^2$.
Since we know the surface area, we have to write an equation for $latex r$ with respect to A: $latex r=\sqrt{\frac{A_{s}}{4\pi}}$. Its derivative is:
$$\dfrac{dr}{dA_{s}}=\frac{1}{4\sqrt{\pi A_{s}}}$$
We have the information $latex \dfrac{dA_{s}}{dt}=2$. Then, applying the chain rule, we have:
$$\dfrac{dr}{dt}=\dfrac{dA_{s}}{dt}\dfrac{dr}{dA_{s}}$$
$$=2 \times \frac{1}{4\sqrt{\pi A_{s}} }$$
$$\dfrac{dr}{dt}=\frac{1}{2\sqrt{\pi A_{s}}}$$
When $latex A_{s}=100\pi$, we have:
$$\frac{dr}{dt}\Big|_{A_{s}=2}=\frac{1}{2\sqrt{100\pi^2}}=\frac{1}{20\pi}$$
The rate of change of the radius when the surface area is 100π is $latex \frac{1}{20\pi}$ cm/s.
EXAMPLE 9
A spherical balloon is inflated at a rate of 10 cm3/s. Find the rate of change of surface area when the radius is 5 cm.
Solution
Representing the radius by $latex r$ and the surface area by $latex A_{s}$, we have $latex V=\frac{4}{3}\pi r^3$ and $latex A_{s}=4\pi r^2$. Then, their derivatives are:
$$\dfrac{dV}{dr}=4\pi r^2$$
$$\dfrac{dA_{s}}{dr}=8\pi r$$
We know that $latex \dfrac{dV}{dt}=10$. Then, using the chain rule, we have:
$$\dfrac{dA_{s}}{dt}=\dfrac{dV}{dt}\dfrac{dA_{s}}{dr}\dfrac{dr}{dV}$$
$$=10 \times 8\pi r \times \frac{1}{4\pi r^2}$$
$$\dfrac{dA_{s}}{dt}=\frac{20}{r}$$
When $latex r=5$, we have:
$$\frac{dA_{s}}{dt}\Big|_{r=5}=\frac{20}{5}=4$$
The rate of change of the surface area when the radius is 5 cm is 4 cm2/s.
EXAMPLE 10
A container has the shape of a hollow cone with a semi-vertical angle of 30° and its vertex pointing downwards.
If water is poured into the cone at the rate of 5 cm3/s, find the rate at which the depth of water in the cone is increasing when its depth is 10 cm.
Solution
We can use the following diagram to facilitate the resolution:
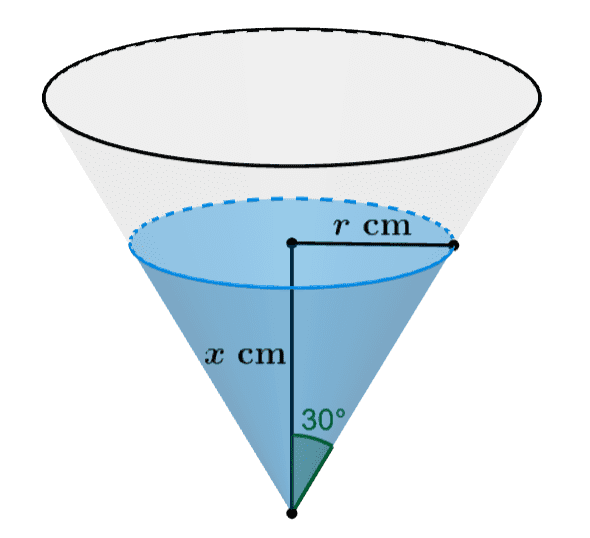
The depth of the water in the cone is represented by $latex x$. Then, the radius $latex r$ of the cross-section of the water is given by:
$$\tan(30^{\circ})=\frac{r}{x}$$
$$r=x\tan(30^{\circ})$$
$$=\frac{x}{\sqrt{3}}$$
The volume of water in the cone is given by:
$$V=\frac{1}{3}\pi r^2x$$
$$=\frac{1}{3}\pi \left(\frac{x}{\sqrt{3}}\right)^2x$$
$$=\frac{1}{9}\pi x^3$$
Then, the derivative of the volume with respect to $latex x$ is:
$$\dfrac{dV}{dx}\pi x^2$$
From the question, we know that $latex \dfrac{dV}{dt}=5$. Also, by the chain rule, we have:
$$\dfrac{dV}{dt}=\dfrac{dV}{dx} \dfrac{dx}{dt}$$
Then,
$$ 5= \frac{1}{3}\pi x^2 \dfrac{dx}{dt}$$
$$ \dfrac{dx}{dt}= \frac{15}{\pi x^2}$$
When $latex x=10$, we have:
$$\dfrac{dx}{dt}=\frac{15}{\pi (10)^2}=\frac{3}{20\pi}$$
The rate of change of depth when the depth is 10 cm is $latex \frac{3}{20\pi}$ cm/s.
Rate of change with derivatives – Practice problems


A hollow cone with a base of radius 10 cm and a height of 10 cm has its vertex pointing downward.
The cone is initially empty when water is poured at a rate of 4π cm3/s. Find the rate at which the depth of the water increases 18 seconds after it began to fill.
Write the answer in the input box.
See also
Interested in learning more about derivatives? You can take a look at these pages: