To find the equation of the normal line to a curve at a given point, we have to use the form y=mx+b where m is the slope and b is the y-intercept. Also, the slope of the normal line is found using the derivative of the function and recalling that the slope of the normal will be equal to -1/m.
Here, we will explore 10 examples with answers of the equation of the normal line to a curve. In addition, we will look at 5 practice problems.
How to find the equation of the normal line to a curve
The normal line to a curve at a point P is the straight line through point P that is perpendicular to the tangent line to the curve at point P.
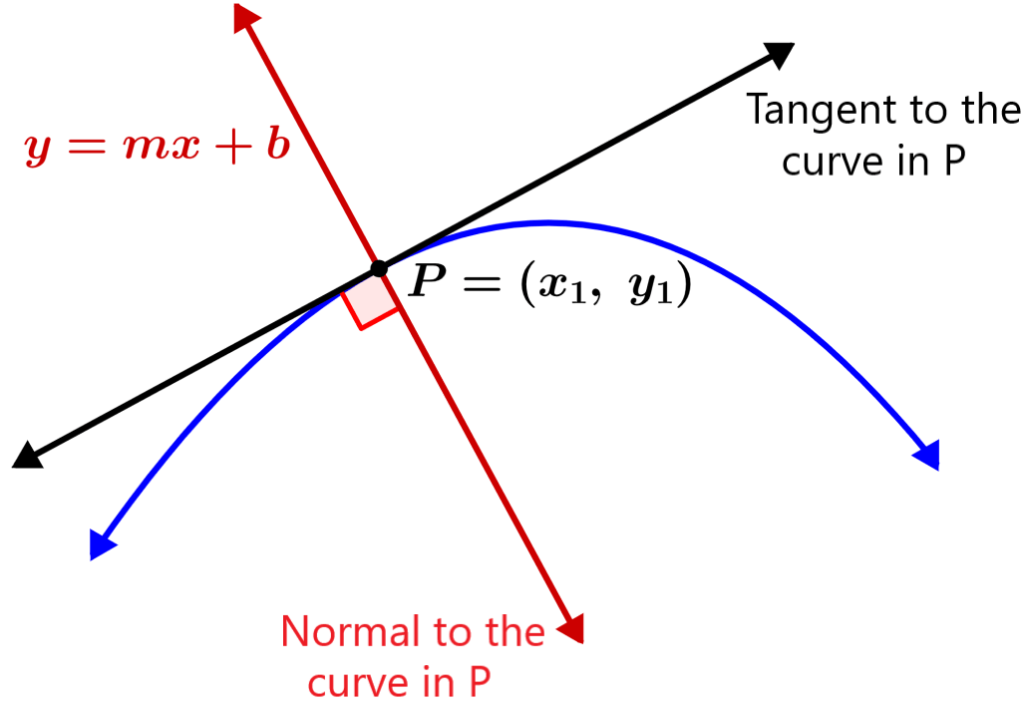
Since the tangent and normal are perpendicular to each other, if the slope of the tangent is $latex m$, then the slope of the normal is equal to $latex -\frac{1}{m}$ .
Therefore, if we want to find the equation of the normal line to a curve at the point $latex (x_{1},~y_{1})$, we can follow these steps:
1. Find the derivative of the function that represents the curve.
2. Find the slope of the tangent line tangent to the curve at point $latex (x_{1},~y_{1})$.
For this, we use the x-coordinate of the point in the derivative of the function. That is, we have $latex m_{1}=f'(x_{1})$.
3. Use the slope from step 2 to find the slope of the normal line to the curve.
The slope of the normal line is equal to $latex m=-\frac{1}{m_{1}}$.
4. Substitute the slope from step 3 in the form $latex y=mx+b$ to find b.
Use the x and y coordinates of the given point to find the value of b. That is, we have $latex y_{1}=mx_{1}=b$.
5. Use the values of m and b in the form $latex y=mx+b$ to obtain the equation of the line.
10 Examples of the normal line to a curve with answers
EXAMPLE 1
Find the equation of the normal line to the function $latex f(x)=x^2$ at the point P=(1, 2).
Solution
We can find the equation of the normal line using the general form $latex y=mx+b$, where m is the slope and b is the y-intercept.
Now, the slope of the normal is equal to $latex -\frac{1}{m_{1}}$, where $latex m_{1}$ is the slope of the tangent line. In turn, the slope of the tangent line is equal to $latex f'(1)$ (we evaluate the derivative at the given point). Then, we have:
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex m_{1}=f'(1)=2(1)$
$latex m_{1}=2$
∴ $latex m=-\frac{1}{2}$
This means we have the equation $latex y=-\frac{1}{2}x+b$. Therefore, we use the point (1, 2) in the equation to determine the value of b:
$latex y=-\frac{1}{2}x+b$
$latex 2=-\frac{1}{2}(1)+b$
$latex b=\frac{5}{2}$
The equation of the normal line at the point (1, 2) is $latex y=-\frac{1}{2}x+\frac{5}{2}$.
EXAMPLE 2
What is the equation of the normal line to the function $latex f(x)=x^3-6x$ at the point (-1, 1)?
Solution
To find the equation of the normal line, we have to start by finding the derivative of the function. Thus, we have:
$latex f(x)=x^3-6x$
$latex f'(x)=3x^2-6$
Now, we can use the derivative to find the slope of the tangent line at the point (-1, 1) by evaluating $latex f'(-1)$:
$latex m_{1}=f'(-1)=3(-1)^2-6$
$latex m_{1}=-3$
The slope of the normal line is equal to $latex m=\frac{1}{3}$. Therefore, we have the equation $latex y=\frac{1}{3}x+b$. Now, we find the value of b, using the point (-1, 1) in the equation:
$latex y=\frac{1}{3}x+b$
$latex 1=\frac{1}{3}(-1)+b$
$latex b=\frac{4}{3}$
The equation of the normal line at the point (-1, 1) is $latex y=\frac{1}{3}x-\frac{4}{3}$.
EXAMPLE 3
If we have the function $latex f(x)=2x^3-7x^2$, find the normal line at the point (2, -3).
Solution
We start by finding the slope of the tangent line. For this, we obtain the derivative of the function:
$latex f(x)=2x^3-7x^2$
$latex f'(x)=6x^2-14x$
The slope of the tangent line at the point (2, 3) is given by $latex f'(2)$:
$latex m_{1}=f'(2)=6(2)^2-14(2)$
$latex m_{1}=24-28$
$latex m_{1}=-4$
The slope of the normal line is $latex m=\frac{1}{4}$. Then, we have the equation $latex y=\frac{1}{4}x+b$. Now, we use this equation with the point (2, -3) to find the value of b:
$latex y=\frac{1}{4}x+b$
$latex -3=\frac{1}{4}(2)+b$
$latex b=-\frac{7}{2}$
The equation of the normal line at the point (2, -3) is $latex y=\frac{1}{4}x-\frac{7}{2}$.
EXAMPLE 4
Find the equation of the normal line to the function $latex f(x)=x^3+\frac{6}{x}$ at the point (1, -2).
Solution
The derivative of the function is:
$latex f(x)=x^3+6x^{-1}$
$latex f'(x)=3x^2-6x^{-2}$
$latex f'(x)=3x^2-\frac{6}{x^2}$
Now, we use the derivative to find the slope of the tangent at the point (1, -2). This is equal to $latex f'(1)$:
$latex m_{1}=f'(1)=3(1)^2-\frac{6}{1^2}$
$latex =3-6$
$latex m_{1}=-3$
The slope of the normal line is $latex m=\frac{1}{3}$. Therefore, we have the equation $latex y=\frac{1}{3}x+b$. Then, we use the point (1, -2) to find the value of b:
$latex y=\frac{1}{3}x+b$
$latex -2=\frac{1}{3}(1)+b$
$latex b=-\frac{7}{3}$
The equation of the normal line at the point (1, -2) is $latex y=\frac{1}{3}x-\frac{7}{3}$.
EXAMPLE 5
Find the normal line to $latex f(x) = -x^{-2}+\sqrt{x}$ at the point (1, -2).
Solution
We have to start by finding the derivative of the given function:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
Now, we use the derivative to find the slope of the tangent at the point (1, -2). This is equal to $latex f'(1)$:
$$m_{1}=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m_{1}=\frac{5}{2}$
The slope of the normal line is $latex m=-\frac{2}{5}$. Then, we have the equation $latex y=-\frac{2}{5}x+b$, so we use the point (1, -2) to find the value of b:
$$y=-\frac{2}{5}x+b$$
$$-2=-\frac{2}{5}(1)+b$$
$latex b=-\frac{8}{5}$
The equation of the normal line at the point (1, -2) is $latex y=-\frac{2}{5}x-\frac{8}{5}$.
EXAMPLE 6
Find the normal line to the function $latex f(x)=\sin(x)-\cos(x)$ at the point (0, 1).
Solution
The derivative of the function is:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
The slope of the tangent line at the point (0, 1) is equal to $latex f'(0)$. Then, we have:
$latex m_{1}=f'(0)=\cos(0)+\sin(0)$
$latex m_{1}=1+0$
$latex m_{1}=1$
The slope of the normal line is equal to $latex m=-1$. Therefore, we have the equation $latex y=-x+b$ and now we use this equation with the point (0, 1) to find the value of b:
$latex y=-x+b$
$latex 1=-0+b$
$latex b=1$
The equation of the normal line at the point (0, 1) is $latex y=-x+1$.
EXAMPLE 7
What is the equation of the normal line to the function $latex f(x)=-2\sin(2x)+\cos(3x)$ at the point (0, 1)?
Solution
The derivative of the function is:
$latex f(x)=-2\sin(2x)+\cos(3x)$
$latex f'(x)=-4\cos(2x)-3\sin(3x)$
Using the derivative, we can find the slope of the tangent line at (0, 1) by evaluating $latex f'(0)$:
$latex m_{1}=f'(0)=-4\cos(2(0))-3\sin(3(0))$
$latex m_{1}=-4+0$
$latex m_{1}=-4$
The slope of the normal line is $latex m=\frac{1}{4}$. Therefore, we have the equation $latex y=\frac{1}{4}x+b$. Now, we use this equation with the point (0, 1) to determine the value of b:
$latex y=\frac{1}{4}x+b$
$latex 1=0+b$
$latex b=1$
The equation of the normal line at the point (0, 1) is $latex y=\frac{1}{4}x+1$.
EXAMPLE 8
Find the normal line to $latex f(x)=x^2-3x+1$ at the point where the curve intersects the y-axis.
Solution
We start by finding the derivative of the function:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
We don’t know the coordinates of the point directly, but we do know that the line is normal to the point where the curve intersects the y-axis. This happens when the coordinates in x are equal to 0. Thus, we have:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Therefore, the point is (0, 1). Now, we use the derivative of the function to evaluate $latex f'(0)$ and find the slope of the tangent:
$latex m_{1}=f'(0)=2(0)-3$
$latex m_{1}=-3$
The slope of the normal line is $latex m=\frac{1}{3}$. Therefore, we have the equation $latex y=\frac{1}{3}x+b$. Using the point (0, 1) we find the value of b:
$latex y=\frac{1}{3}x+b$
$latex 1=\frac{1}{3}(0)+b$
$latex b=1$
The equation of the normal line at the point (0, 1) is $latex y=\frac{1}{3}x+1$.
EXAMPLE 9
Find the equations of the two normal lines to the function $latex f(x)=x^2-5x+4$ at the points where the function intersects the x-axis.
Solution
We have to start by finding the points where the function intersects the x-axis. This happens when the value of y is 0. Therefore, we have:
$latex x^2-5x+4=0$
$latex (x-4)(x-1)=0$
The function cuts the x-axis when $latex x=4$ and $latex x=1$. This means that we have the points (4, 0) and (1, 0).
Now, we use the derivative of the function to find the slopes of the tangent lines by evaluating $latex f'(4)$ and $latex f'(1)$:
$latex f(x)=x^2-5x+4$
$latex f'(x)=2x-5$
$latex f'(4)=2(4)-5=3$
$latex f'(1)=2(1)-5=-3$
The slopes of the normal lines are $latex m_{1}=-\frac{1}{3}$ and $latex m_{2}=\frac{1}{3}$. Thus, we use the form $latex y=mx+b$ with the slopes found and the coordinates of each point to determine the values of b:
$latex 0=\frac{1}{3}(4)+b_{1}$
$latex b_{1}=-\frac{4}{3}$
$latex 0=-\frac{1}{3}(1)+b_{2}$
$latex b_{2}=\frac{1}{3}$
The equations of the normal lines are $latex y=-\frac{1}{3}x-\frac{4}{3}$ and $latex y=\frac{1}{3}x+\frac{ 1}{3}$.
EXAMPLE 10
Find the two normal lines to the function $latex f(x)=x^2$ at the points where $latex y=9$.
Solution
We have that the lines are normal at the points where $latex y=9$. This means that we have to find the values of x when $latex y=9$:
$latex x^2=9$
$latex x=\pm \sqrt{9}$
$latex x=3~~$ or $latex ~~x=-3$
Now that we know the coordinates of the points, we use the derivative of the function to find the slopes of the tangent lines by evaluating $latex f'(3)$ and $latex f'(-3)$.
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex f'(3)=2(3)=6$
$latex f'(-3)=2(-3)=-6$
The slopes of the normal lines are $latex m_{1}=-\frac{1}{6}$ and $latex m_{2}=\frac{1}{6}$.
Now, we use the form $latex y=mx+b$ with the slopes found and the coordinates of each point (the y values are 9 in both cases) to find the values of b:
$latex 9=-\frac{1}{6}(3)+b_{1}$
$latex b_{1}=\frac{19}{2}$
$latex 9=\frac{1}{6}(-3)+b_{2}$
$latex b_{2}=\frac{19}{2}$
The equations of the normal lines are $latex y=-\frac{1}{6}x+\frac{19}{2}$ and $latex y=\frac{1}{6}x+\frac{19 }{2}$.
Normal line to a curve – Practice problems


What is the equation of the normal line to the function $latex f(x)=2\sqrt{x}$ where $latex x=9$?
Write the equation in the input box.
See also
Interested in learning more about equations of tangent and normal lines to functions? You can take a look at these pages:



