Cosine Calculator (Degrees and Radians)
Result:
Graph of cosine
This calculator allows you to find the cosine of an entered angle. When entering an angle, the calculator will immediately display the value of its cosine. You can use both degrees and radians.
Below you can find important information related to cosine. You will find the definition of cosine, its graph with the most fundamental characteristics, and the cosine values of important angles.
How to use the cosine calculator?
Step 1: Select the type of angle you want to enter. Click the blue button to select between using degrees, radians, or π radians.
Step 2: Enter the angle in the corresponding box. You can use positive and negative numbers.
Step 3: The cosine of the entered angle will be displayed in the right panel.
What is the difference between degrees, radians, and π radians on the calculator?
One complete revolution is equal to 360° or 2π radians. This means that 180° is equivalent to π radians.
Also, π is a constant that indicates the ratio of the diameter to the circumference of a circle. Its approximate value is 3.1415… So, π radians is approximately 3.1415 radians.
Suppose we want to input the angle 45°. In the calculator, we have the following options:
- We can select “degrees” and enter 45.
- We can select “π radians” and enter 0.25 (180° equals π radians, so 45° equals 1/4 π radians).
- We can select “radians” and enter 0.7854 (0.25π radians equals 0.7854 radians).
What is the cosine of an angle?
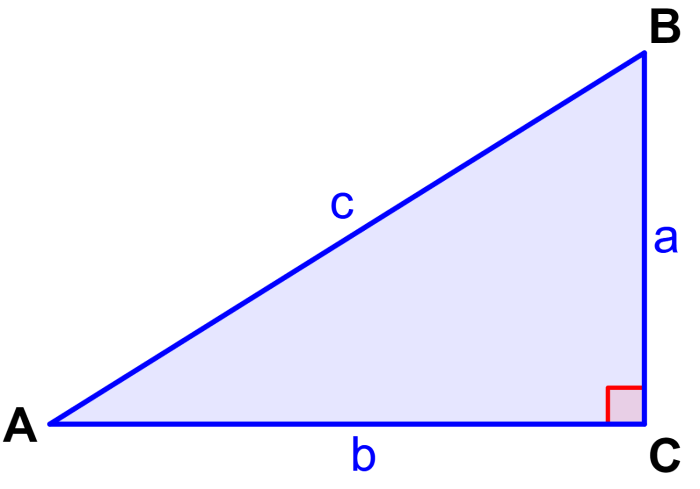
The cosine of an angle can be defined by referring to a right triangle. Therefore, the cosine is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse of the triangle.
For example, in the following right triangle, the cosine of angle A is equal to the length of side b (side adjacent to A) divided by the length of side c (hypotenuse and opposite the right angle).
Similarly, the cosine of angle B is equal to the length of side a (side adjacent to B) divided by the length of side c (hypotenuse).
If you want to learn more about the cosine of an angle, you can visit our article Cosine of an Angle – Formulas and Examples.
Graph of the cosine of an angle
Although cosine is defined using a right triangle, its definition can be extended to encompass angles that go beyond angles found in a triangle.
The cosine is a periodic function, which means that it repeats itself after a fixed interval. In this case, the cosine function repeats every 360° or 2π.
Domain of the cosine of an angle
Using the graph of cosine, we can easily deduce that the cosine function can take any input value (usually x values) both positive and negative. Therefore, the domain of the cosine function is equal to all real numbers.
Range of the cosine of an angle
Using the cosine graph, we can see that the output values of the function range from -1 to 1. This means that the range of the cosine function is equal to -1 ≤ cos(α) ≤ 1.
Table of cosines of common angles
| Degrees | Radians | Cosine |
|---|---|---|
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
Related calculators:
- Sine Calculator (Degrees and Radians)
- Tangent Calculator (Degrees and Radians)
- Secant Calculator (Degrees and Radians)
- Cosecant Calculator (Degrees and Radians)
- Cotangent Calculator (Degrees and Radians)
You can explore other calculators here.
