Cosecant Calculator (Degrees and Radians)
Result:
Graph of cosecant
Use this calculator to find the cosecant of any angle. You can use degrees, radians, and π radians. When entering an angle in the box, the cosecant will be displayed immediately.
Below you can find additional information on how to use the cosecant calculator. Also, you have information to learn about the cosecant of an angle in general.
How to use the cosecant calculator?
Step 1: Select the type of angle you want to enter. Click the blue button to select between degrees, radians, and π radians.
Step 2: Write the angle in the corresponding input box. You can use positive and negative angles.
Step 3: The entered angle and its cosecant will be displayed in the right panel.
Difference between using degrees, radians and π radians in calculator
We can remember that a complete circle has a total of 360° or also 2π radians. Therefore, we can deduce that π radians is equal to 180°.
Now, the only difference between using radians and π radians is that “π radians” multiplies any value entered by π. That is, if we enter 2.5, we will be calculating the cosecant of 2.5π radians.
Therefore, to enter 0.25π, we can select the “π radians” option and simply enter 0.25. Or alternatively, we can select the “radians” option and enter 0.7854, which is equivalent to 0.25π, since π has a value of approximately 3.1415…
What is the cosecant of an angle?
The cosecant of an angle is the reciprocal function of the sine of an angle. This means that the cosecant is equal to 1 over the sine of an angle.
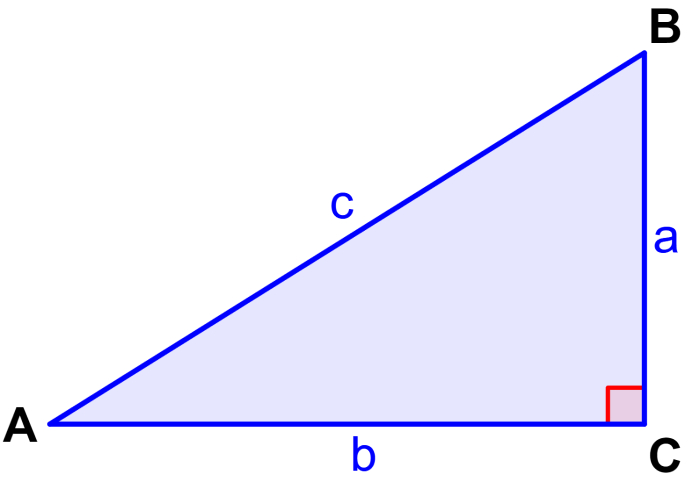
Alternatively, the cosecant can also be defined in terms of the sides of a right triangle. Therefore, the cosecant of an angle is equal to the hypotenuse on the opposite side.
For example, using the following right triangle, we can define the cosecant of angle A to be the length of side c (hypotenuse) divided by the length of side a (side opposite angle A).
In addition, we can define the cosecant of angle B as the length of side c (hypotenuse) divided by the length of side b (side opposite angle B).
If you want to learn more about the cosecant of an angle, visit our article Cosecant of an Angle – Formulas and Examples.
Why is the cosecant of 0° and 180° undefined?
The angles 0° and 180° are undefined because the cosecant is the reciprocal function of sine. If we use those angles in the calculator, we will get “Undefined”.
Since the cosecant is equivalent to 1 over the sine of the angle, all the angles that result in a sine equal to 0 will be undefined, since we cannot have 0 in the denominator of a fraction.
The sine is equal to 0 when the angle is equal to 0°. Also, the sine function is periodic, so the value repeats every time we add 180°n, where n is any positive or negative integer.
For example, the sine of 0°+180°(2)=360°, is also equal to 0, so the cosecant of 360° is undefined.
Graph of the cosecant of an angle
The cosecant can be found using angles that go beyond the angles found in a right triangle. That is, we can find the cosecant of angles greater than 180°, both positive and negative.
The cosecant function is periodic. Therefore, the graph of cosecant repeats itself after a constant interval. The period of the cosecant function is equal to 360° or 2π.
Domain of the cosecant of an angle
Using the graph of cosecant, we can deduce that the cosecant can take input values that extend to both positive and negative infinity.
However, the cosecant function approaches infinity at some input values. This means that the function forms asymptotes at those points and produces undefined values.
The values that we cannot use are equal to 180°n, where n is a positive or negative integer. Therefore, the domain of the cosecant function is equal to all real numbers except 180°n or πn.
Range of the cosecant of an angle
Using the graph of cosecant, we can see that the function can result in any value, both positive and negative, not including values between -1 and 1.
Therefore, the range of the cosecant is equal to the real numbers from 1 to infinity and from -1 to negative infinity.
Table of cosecants of common angles
| Degrees | Radians | Cosecant |
| 90° | 1 | |
| 60° | ||
| 45° | ||
| 30° | ||
| 0° | 0 | Undefined |
Related calculators:
- Cosine Calculator (Degrees and Radians)
- Sine Calculator (Degrees and Radians)
- Tangent Calculator (Degrees and Radians)
- Secant Calculator (Degrees and Radians)
- Cotangent Calculator (Degrees and Radians)
You can explore other calculators here.
