The cosine of an angle is found by relating the sides of a right triangle. The cosine is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse. The cosine is also equal to the sine of the complementary angle. The cosine values of the most important angles can be obtained using the proportions of the known triangles.
Here, we will learn about the cosine of angles in more detail and we will solve some practice problems.
Definition of the cosine of an angle
The cosine of an angle of a right triangle is defined as the length of the side adjacent to the angle divided by the length of the hypotenuse of the triangle.
Additionally, the cosine of an angle is defined as the sine of the complementary angle. The complementary angle is equal to the given angle subtracted from 90° (a right angle). For example, if we have the angle 40°, its complement is 50°. Therefore, for any angle θ, we have:
$latex \cos (\theta)=\sin (90^{\circ}-\theta)$
In terms of radians, we have:
$latex \cos (\theta)=\sin (\frac{\pi}{2}-\theta)$
Right triangles and cosines
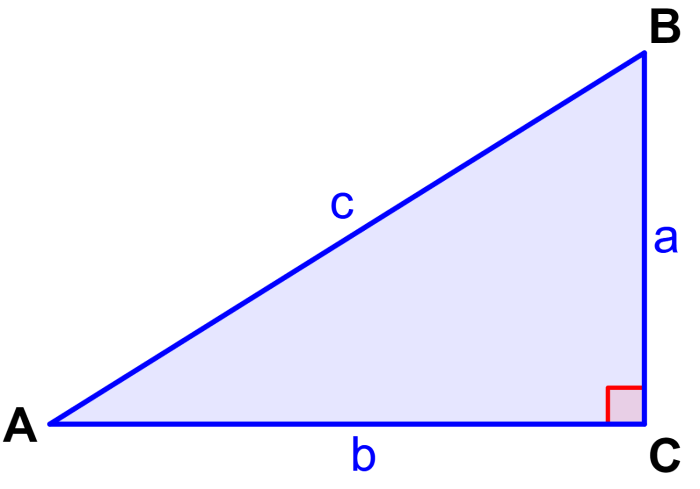
Let’s look at the right triangle ABC that has a right angle at C.
Generally, we use the letter a to denote the side that is opposite angle A, we use the letter b to denote the side that is opposite angle B, and we use the letter c to denote the side that is opposite angle C.
Since the sum of the interior angles of a triangle is equal to 180° and the angle C measures 90°, we know that angles A and B are complementary, that is, they add up to 90°. This means that the cosine of B is equal to the sine of A.
The cosine of an angle in a right triangle is equal to the adjacent side divided by the hypotenuse:
| $latex \cos=\frac{\text{adjacent}}{\text{hypotenuse}}$ |
In the above triangle, we have $latex \cos(A)=\frac{b}{c}$, and also $latex \cos(B)=\frac{a}{c}$.
Cosines for common special angles
We can obtain the result of cosines of special angles based on the proportions of the sides. For example, the 45° angle is found in a right isosceles triangle, which has the angles 45°-45°-90°.
We know that right triangles have the relationship $latex {{c}^2}={{a}^2}+{{b}^2}$, but in this case, $latex a = b$, so we have $latex {{c}^2}= 2{{a}^2}$. This means that we have $latex c= a \sqrt{2}$.
Therefore, both the sine and cosine of 45° are equal to $latex \frac{1}{\sqrt{2}}$, which can be written as $latex \frac{\sqrt{2}}{2}$.
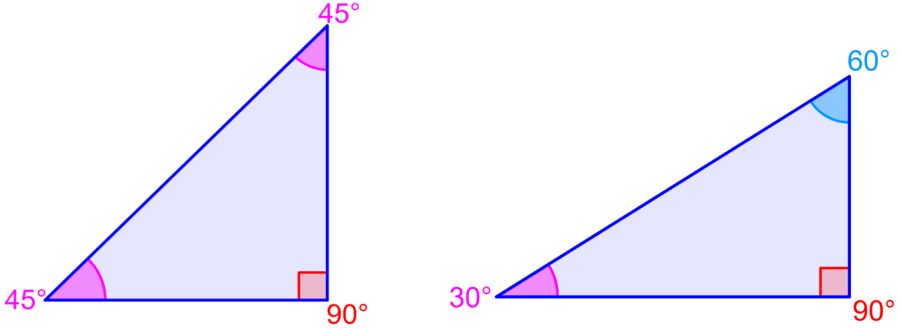
In the case of the right triangle with angles 30°-60°-90°, the proportions of its sides are 1:$latex \sqrt{3}$:2. Using these proportions, we have $latex \sin(30^{\circ}) = \cos(60^{\circ}) = \frac{1}{2}$ and we also have $latex \sin(60^{\circ})=\cos(30^{\circ}) = \frac{\sqrt{3}}{2}$.
| Degrees | Radians | Cosine |
| 90° | $latex \frac{\pi}{2}$ | 0 |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{1}{2}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{\sqrt{3}}{2}$ |
| 0° | 0 | 1 |
Cosine of an angle – Examples with answers
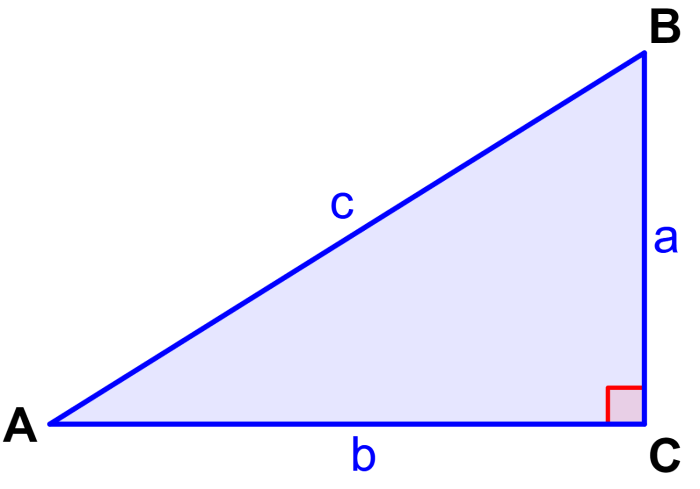
The following examples can be used to follow the process used to solve problems related to cosines. These and the following examples refer to the right triangle used above.
EXAMPLE 1
If we have $latex \cos(A)=0.2$ and $latex b = 3$, what is the value of $latex c$?
Solution
Referring to the right triangle above, we see that we have $latex \cos (A) = \frac{b}{c}$. We can use the values given in this equation and solve for c:
$latex \cos(A)=\frac{b}{c}$
$latex 0.2=\frac{3}{c}$
$latex c=\frac{3}{0.2}$
$latex c=15$
The value of the hypotenuse is 15.
EXAMPLE 2
If we have $latex a=10$ and $latex \cos(B)=\frac{1}{3}$, find the value of $latex c$.
Solution
From the right triangle above, we can deduce that we have $latex \cos(B) = \frac{a}{c}$. Using the values given in the formula and solving for c, we have:
$latex \cos(B)=\frac{a}{c}$
$latex \frac{1}{3}=\frac{10}{c}$
$latex c=3(10)$
$latex c=30$
The value of the hypotenuse is 30.
EXAMPLE 3
What is the value of A if we have $latex b=5$ and $latex c=8$?
Solution
We can form the following relationship $latex \cos(A)=\frac{b}{c}$. Therefore, using the given values, we have:
$latex \cos(A)=\frac{b}{c}$
$latex \cos(A)=\frac{5}{8}$
$latex \cos(A)=0.625$
Now, we use the function $latex {{\cos}^{-1}}$ on a calculator to get the result:
$latex {{\cos(0.625)}^{-1}}=51.3$°
Angle A measures 51.3°.
→ Cosine Calculator (Degrees and Radians)
Cosine of an angle – Practice problems
Practice what you have learned about the cosine of an angle to solve the following practice problems. If you need help with this, you can look at the examples with answers above.
See also
Interested in learning more about the cosine of an angle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
