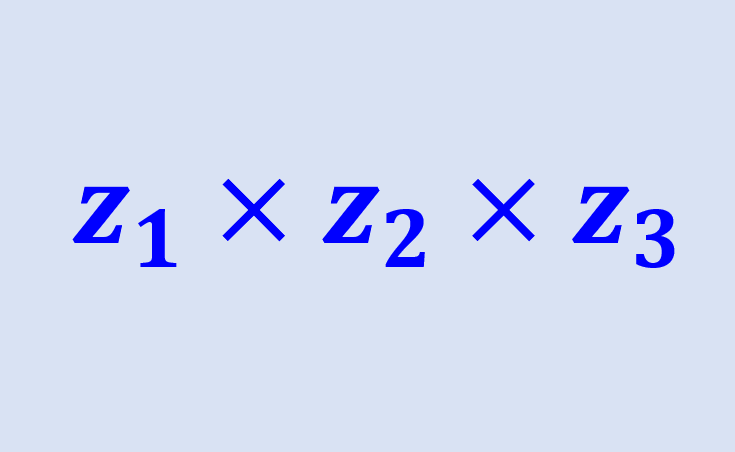Complex number multiplication exercises can be solved using the distribution method of multiplication, similar to that used when multiplying two binomials. The difference is that, when we have the imaginary unit squared, i², we have to remember that this is equal to -1.
Here, we will learn to multiply complex numbers. We will look at several examples with answers to understand how to use the multiplication method mentioned.
How to multiply complex numbers?
Complex number multiplications are solved using a method very similar to when we multiply two binomials. The only difference is the introduction of the imaginary unit:
$latex \sqrt{-1}=i$
Something important to keep in mind is that, when we square the imaginary unit, we have:
$latex {{(\sqrt{-1})}^2}={{(i)}^2}$
$latex -1={{i}^2}$
For example, if we have the multiplication of complex numbers $latex z_{1}=a+bi$ and $latex z_{2}=c+di$, we can get their product as follows:
$latex z_{1}z_{2}=(a+bi)(c+di)$
$latex =ac+adi+cbi+bd{{i}^2}$
$latex =ac+(ad+cb)i+bd(-1)$
$latex =ac+(ad+cb)i-bd$
Multiplication of complex numbers – Examples with answers
The solving process mentioned above is used to solve the following complex number multiplication exercises. It is recommended that you try to solve the exercises yourself before looking at the solution.
EXAMPLE 1
Find the product of the complex numbers: $latex (4+2i)(2+3i)$.
Solution
This is similar to multiplying two binomials. We expand the multiplication and then combine like terms:
$latex (4+2i)(2+3i)$
$$=(4)(2)+(4)(3i)+(2i)(2)+(2i)(3i)$$
$latex =8+12i+4i+6{{i}^2}$
$latex =8+16i+6{{i}^2}$
Now, we have to substitute $latex {{i}^2}$ with $latex -1$ and combine like terms again:
$latex =8+16i+6(-1)$
$latex =8+16i-6$
$latex =2+16i$
EXAMPLE 2
What is the product of $latex (4-5i)(2-7i)$?
Solution
We have to expand the multiplication and then combine like terms:
$latex (4-5i)(2-7i)$
$$=(4)(2)+(4)(-7i)+(-5i)(2)+(-5i)(-7i)$$
$latex =8-28i-10i+35{{i}^2}$
$latex =8-38i+35{{i}^2}$
Recall that $latex {{i}^2}$ is equal to $latex -1$. We combine like terms again:
$latex =8-38i+35(-1)$
$latex =8-38i-35$
$latex =-27-38i$
EXAMPLE 3
If we have $latex z_{1}=6-5i$ and $latex z_{2}=-4+7i$, what is the result of $latex z_{1}z_{2}$?
Solution
We form the multiplication, expand it, and then combine like terms:
$latex (6-5i)(-4+7i)$
$$=(6)(-4)+(6)(7i)+(-5i)(-4)+(-5i)(7i)$$
$latex =-24+42i+20i-35{{i}^2}$
$latex =-24+62i-35{{i}^2}$
We acknowledge that $latex {{i}^2}$ is equal to $latex -1$ and we combine like terms again:
$latex =-24+62i-35(-1)$
$latex =-24+62i+35$
$latex =11+62i$
EXAMPLE 4
Find the product of the following complex number and its conjugate: $latex 4-3i$.
Solution
The conjugate of a complex number is found by changing the sign of the imaginary component. In this case, the conjugate of $latex 4-3i$ is $latex 4+3i$. Now, we can multiply them to get the product:
$latex (4-3i)(4+3i)$
$$=(4)(4)+(4)(3i)+(-3i)(4)+(-3i)(3i)$$
$latex =16+12i-12i-9{{i}^2}$
$latex =16-9{{i}^2}$
We substitute $latex {{i}^2}$ with $latex -1$ and combining like terms, we have:
$latex =16-9(-1)$
$latex =16+9$
$latex =25$
EXAMPLE 5
Multiply the number $latex -1-i$ by itself.
Solution
Multiplying the number by itself, we have:
$latex (-1-i)(-1-i)$
$$=(-1)(-1)+(-1)(-i)+(-i)(-1)+(-i)(-i)$$
$latex =1+i+i+{{i}^2}$
$latex =1+2i+{{i}^2}$
Substituting $latex {{i}^2}$ by $latex -1$ and combining like terms, we have:
$latex =1+2i+(-1)$
$latex =2i$
EXAMPLE 6
Solve the multiplication $latex (3i-5{{i}^2})(5i+4{{i}^2})$.
Solution
In this case, we have an expression with $latex {{i}^2}$, so we can start simplifying by replacing $latex {{i}^2}$ with $latex -1$. Therefore, we have:
$latex (3i-5{{i}^2})(5i+4{{i}^2})$
$latex =(3i-5(-1))(5i+4(-1))$
$latex =(3i+5)(5i-4)$
$$=(3i)(5i)+(3i)(-4)+(5)(5i)+(5)(-4)$$
$latex =15{{i}^2}-12i+25i-20$
$latex =15{{i}^2}+13i-20$
Again, we replace $latex {{i}^2}$ with $latex -1$ and we combine like terms:
$latex =15(-1)+13i-20$
$latex =-15+13i-20$
$latex =-35+13i$
Multiplication of complex numbers – Practice problems
Put into practice your knowledge about the multiplication of complex numbers and solve the following problems. Select an answer and check it to make sure you selected the correct one. If you need help, you can look at the solved examples above.
See also
Interested in learning more about operations with complex numbers? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
