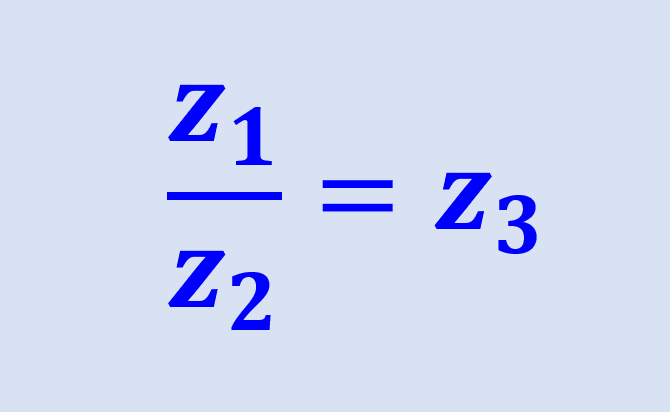The division of complex numbers is solved by multiplying both the numerator and denominator by the conjugate of the complex number in the denominator. This will allow us to obtain a real number in the denominator and we will obtain the result to the division.
Here, we will learn how to divide complex numbers using their conjugate. Also, we will look at several examples with answers to look at the application of this process.
How to divide complex numbers?
To divide complex numbers, we have to start by writing the problem in fractional form. Then, we have to multiply both the numerator and denominator by the conjugate of the denominator.
Remember that to find the conjugate of the denominator, we simply have to change the sign to the imaginary component. For example, the conjugate of $latex a+bi$ is $latex a-bi$.
Therefore, if we want to divide the number $latex a+bi$ by the number $latex c+bi$, we form the following expression:
| $latex \frac{a+bi}{c+di}=\frac{a+bi}{c+di}\times \frac{c-di}{c-di}$ |
We solve this expression by distributing the multiplication in both the numerator and denominator. Then, we simplify the powers of i, specifically, we remember that $latex {{i}^2}$ is equal to $latex -1$.
Then, we combine like terms to simplify the obtained expression, and finally, we write the answer in the form $latex a+bi$.
Division of complex numbers – Examples with answers
The following exercises use the process detailed above to solve the divisions of complex numbers. Each example has its respective solution, but it is recommended that you try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
Divide the complex numbers: $latex (2+4i) \div (1+2i)$.
Solution
We have to start by writing the original problem in fractional form:
⇒ $latex \frac{2+4i}{1+2i}$
Now, we multiply both the numerator and denominator by the conjugate of the denominator. In this case, the conjugate of the denominator is $latex 1-2i$. Therefore, we have:
$latex \frac{2+4i}{1+2i}=\frac{2+4i}{1+2i}\times \frac{1-2i}{1-2i}$
We expand the multiplication of the numerator and denominator and simplify by combining like terms:
$latex = \frac{2-4i+4i-8{{i}^2}}{1-2i+2i-2{{i}^2}}$
$latex = \frac{2-8{{i}^2}}{1-4{{i}^2}}$
We remember that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{2-8(-1)}{1-4(-1)}$
$latex = \frac{10}{5}$
$latex =2$
EXAMPLE 2
Divide the complex numbers: $latex (5+10i) \div (4+3i)$.
Solution
We rewrite complex numbers in fractional form:
⇒ $latex \frac{5+10i}{4+3i}$
Here, the conjugate of the denominator is $latex 4-3i$. Therefore, we multiply the numerator and denominator by this conjugate:
$latex \frac{5+10i}{4+3i}=\frac{5+10i}{4+3i}\times \frac{4-3i}{4-3i}$
We solve the multiplications in the numerator and denominator and simplify:
$latex = \frac{20-15i+40i-30{{i}^2}}{16-12i+12i-9{{i}^2}}$
$latex = \frac{20+25i-30{{i}^2}}{16-9{{i}^2}}$
We recall that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{20+25i-30(-1)}{16-9(-1)}$
$latex = \frac{50+25i}{25}$
We already got the answer, but we have to write it in the form $latex a+bi$. Thus, we have:
$latex =\frac{50}{25}+\frac{25}{25}i$
$latex =2+i$
EXAMPLE 3
What is the result of the division $latex (4-6i)\div (-2-4i)$?
Solution
We have to write the division in fractional form:
⇒ $latex \frac{4-6i}{-2-4i}$
The conjugate of the denominator is $latex -2+4i$. Therefore, we have:
$latex \frac{4-6i}{-2-4i}=\frac{4-6i}{-2-4i}\times \frac{-2+4i}{-2+4i}$
Now, we solve the multiplications in the numerator and denominator and simplify:
$latex = \frac{-8+16i+12i-24{{i}^2}}{4-8i+8i-16{{i}^2}}$
$latex = \frac{-8+28i-24{{i}^2}}{4-16{{i}^2}}$
We remember that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{-8+28i-24(-1)}{4-16(-1)}$
$latex = \frac{16+28i}{20}$
Writing in the form $latex a+bi$, we have:
$latex =\frac{16}{20}+\frac{28i}{20}$
$latex =\frac{4}{5}+\frac{7i}{5}$
EXAMPLE 4
What is the result of the division $latex (-4-4i) \div (-4+4i)$?
Solution
The division in fractional form is:
⇒ $latex \frac{-4-4i}{-4+4i}$
If we multiply both the numerator and the denominator by the conjugate of the denominator, which is $latex -4-4i$, we have:
$latex \frac{-4-4i}{-4+4i}=\frac{-4-4i}{-4+4i}\times \frac{-4-4i}{-4-4i}$
We expand the multiplication of the numerator and denominator and simplify by combining like terms:
$latex = \frac{16+16i+16i+16{{i}^2}}{16+16i-16i-16{{i}^2}}$
$latex = \frac{16+32i+16{{i}^2}}{16-16{{i}^2}}$
We recall that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{16+32i+16(-1)}{16-16(-1)}$
$latex = \frac{32i}{32}$
$latex =i$
EXAMPLE 5
Solve the division $latex \frac{10-2i}{-4+5i}$.
Solution
In this case, we already have the division written in fractional form, so we start by multiplying both the numerator and the denominator by the conjugate of the denominator.
In this case, the conjugate of the denominator is $latex -4-5i$. Therefore, we have:
$latex \frac{10-2i}{-4+5i}=\frac{10-2i}{-4+5i}\times \frac{-4-5i}{-4-5i}$
We solve the multiplications in the numerator and denominator:
$latex = \frac{-40-50i+8i+10{{i}^2}}{16+20i-20i-25{{i}^2}}$
$latex = \frac{-40-32i+10{{i}^2}}{16-25{{i}^2}}$
We use the fact that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{-40-32i+10(-1)}{16-25(-1)}$
$latex = \frac{-50-32i}{41}$
$latex =-\frac{50}{41}-\frac{32}{41}i$
EXAMPLE 6
Solve the division $latex \frac{-4}{1-i}$.
Solution
Here we already have a division in fractional form, so we start by multiplying both the numerator and the denominator by the conjugate of the denominator.
In this case, the conjugate of the denominator is $latex 1+i$. Therefore, we have:
$latex \frac{-4}{1-i}=\frac{-4}{1-i}\times \frac{1+i}{1+i}$
Now, we distribute to the multiplications and simplify:
$latex = \frac{-4-4i}{1+i-i-{{i}^2}}$
$latex = \frac{-4-4i}{1-{{i}^2}}$
Recall that $latex {{i}^2}$ is equal to $latex -1$:
$latex = \frac{-4-4i}{1+1}$
$latex = \frac{-4-4i}{2}$
$latex =-\frac{4}{2}-\frac{4}{2}i$
$latex =-2-2i$
Division of complex numbers – Practice problems
Practice what you have learned about the division of complex numbers with the following problems. If you need help with these problems, you can look at the solved examples above.
See also
Interested in learning more about operations with complex numbers? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
