Like terms are terms of algebraic expressions that have the same variables with the same exponents. These terms can be added to simplify an algebraic expression. Constant terms are also considered like terms.
Here, we will look at a definition of like terms. Then, we will solve some exercises of combining like terms in algebraic expressions.
Definition of like terms in algebraic expressions
Like terms are algebraic terms that contain the same variables raised to the same powers. These terms can be added when simplifying algebraic expressions.
Two or more like terms may or may not have the same coefficients. For two algebraic terms to be like, they must have the same variables with the same exponents.
Let’s recall that variables are the “letters” of an algebraic term and the coefficients are the numbers that multiply the variables.
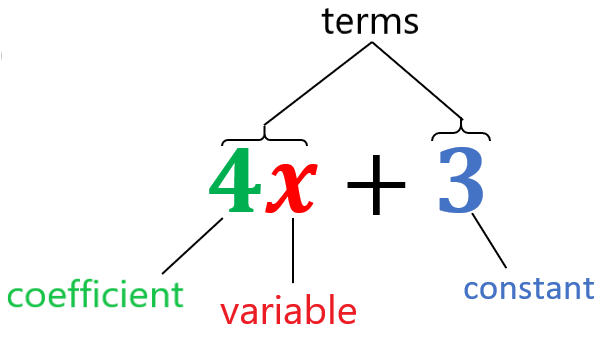
Constant terms, that is, terms that have no variables, are also considered like terms.
The following are some examples of like and unlike terms:
Like terms
- $latex 2x^2~$ and $latex ~4x^2$
- $latex 4x^2y~$ and $latex ~2x^2y$
- $latex x^3z~$, $latex ~4x^3z~$ and $latex ~3x^3z~$
Unlike terms
- $latex 2x^2~$ and $latex ~2x$
- $latex 3x^2y~$ and $latex ~2x^2$
- $latex x^2z$ ~and $latex ~4x^3z$
10 Examples with answers of like terms
EXAMPLE 1
Determine the terms that are like terms of $latex 6x^2$.
$latex 2x^2~~$ $latex ~~5x~~$ $latex ~~3x^3~~$ $latex ~~4x^2$
Solution
The given term is $latex 6x^2$. We note that it has a variable, x, raised to the power of 2. Then, we analyze each of the given terms
- $latex 2x^2$ has the same variable x, raised to the power of 2. It is a like term.
- $latex 5x$ has the same variable x, but it is not raised to the power of 2. It is not a like term.
- $latex 3x^3$ has the same variable x, but it is not raised to the power of 2. It is not a like term.
- $latex 4x^2$ has the same variable x, raised to the power of 2. It is a like term.
The like terms of $latex 6x^2$ are $latex 2x^2~$ and $latex ~4x^2$.
EXAMPLE 2
Which of the following are like terms of $latex 2xy^2$?
$latex 3xy^2~~$ $latex ~~2xy~~$ $latex ~~5xy^3~~$ $latex ~~4xz^2$
Solution
We want terms with $latex xy^2$. Analyzing each of the given terms, we have:
- $latex 3xy^2$ has the same variables with the same exponents. It is a like term.
- $latex 2xy$ has the same variables, but with different exponents. It is not a like term.
- $latex 5xy^3$ has the same variables, but with different exponents. It is not a like term.
- $latex 4xz^2$ does not have the same variables. It is not a similar term.
The like term of $latex 2xy^2$ is $latex 3xy^2$.
EXAMPLE 3
Identify like terms in $latex -2x^2y$.
$latex 3y^2z~~$ $latex ~~-3xy^2~~$ $latex ~~4x^2y~~$ $latex ~~5x^2z$
Solution
We have to find terms with $latex x^2y$. Then, we have:
- $latex 3y^2z$ does not have the same variables. It is not a like term.
- $latex -3xy^2$ has the same variables, but with different exponents. It is not a like term.
- $latex 4x^2y$ has the same variables with the same exponents. It is a like term.
- $latex 5x^2z$ does not have the same variables. It is not a like term.
The like term of $latex -2x^2y$ is $latex 4x^2y$.
EXAMPLE 4
Which of the following are like terms of $latex 4x^2y^3z$?
$latex 3xy^2z^2~~$ $latex ~~2x^2y^3z~~$ $latex ~~4x^2y^3z^2~~$ $latex ~~-2x^2y^3w$
Solution
In this case, we need to find terms with $latex x^2y^3z$. Looking at each given term, we have:
- $latex 3xy^2z^2$ has the same variables, but with different exponents. It is not a like term.
- $latex 2x^2y^3z$ has the same variables and the same exponents. It is a like term.
- $latex 4x^2y^3z^2$ has the same variables, but with different exponents. It is not a like term.
- $latex -2x^2y^2w$ does not have the same variables. It is not a like term.
The like term of $latex 4x^2y^3z$ is $latex 2x^2y^3z$.
EXAMPLE 5
Combine the like terms of the following expression:
$$2x^2+2x+5x+4x^2+3x+2x^2$$
Solution
To combine like terms, we can start by identifying all the like terms:
- $latex 2x^2~$, $latex ~4x^2~$ and $latex ~2x^2$
- $latex 2x~$, $latex ~5x~$ and $latex ~3x$
Now, we add these terms and we have:
$$(2x^2+4x^2+2x^2)+(2x+5x+3x)$$
$$=8x^2+10x$$
EXAMPLE 6
Simplify the following expression by combining like terms:
$$3y^2+2y+y^2+5+4y+3+2y^2+4$$
Solution
Identifying like terms, we have:
- $latex 3y^2~$, $latex ~y^2~$ and $latex ~2y^2$
- $latex 2y~$ and $latex ~4y~$
- $latex 5~$, $latex ~3~$ and $latex ~4$
Adding the like terms, we have:
$$(3y^2+y^2+2y^2)+(2y+4y)+(5+3+4)$$
$$=6y^2+6y+12$$
EXAMPLE 7
Combine the like terms of the following expression:
$$2x^3+4x-2x^2+4x^2-5x^3+5x-3x^2$$
Solution
We have the following like terms:
- $latex 2x^3~$, and $latex ~-5x^3$
- $latex -2x^2~$, $latex ~4x^2~$ and $latex ~-3x^2$
- $latex 4x~$ and $latex ~5x$
Adding these terms, we have:
$$(2x^3-5x^3)+(-2x^2+4x^2-3x^2)+(4x+5x)$$
$$=-3x^3-x^2+9x$$
EXAMPLE 8
Simplify the following expression by combining like terms:
$$2xy^2+4x^2y+3xy^2+5+4x^2y+3+2xy^2+2$$
Solution
We have the following like terms:
- $latex 2xy^2~$, $latex ~3xy^2~$ and $latex ~2xy^2$
- $latex 4x^2y~$ and $latex ~4x^2y~$
- $latex 5~$, $latex ~3~$ and $latex ~2$
Adding these terms, we have:
$$(2xy^2+3xy^2+2xy^2)+(4x^2y+4x^2y)+(5+3+2)$$
$$=7xy^2+8x^2y+10$$
EXAMPLE 9
Combine the like terms of the following expression:
$$3ab^2-2a^2b+5ab^2-ab+3a^2b+2ab+2ab^2-a^2b$$
Solution
Let’s start by identifying the like terms of the given expression:
- $latex 3ab^2~$, $latex ~5ab^2~$ and $latex ~2ab^2$
- $latex -2a^2b~$, $latex ~3a^2b~$ and $latex ~-a^2b~$
- $latex -ab~$, and $latex ~2ab$
Adding the like terms, we have:
$$(3ab^2+5ab^2+2ab^2)+(-2a^2b+3a^2b-a^2b)+(-ab+2ab)$$
$$=10ab^2+ab$$
EXAMPLE 10
Combine the like terms of the following expression:
$$xyz^2-2x^2yz+5xy^2z+4x^2yz+3xy^2z-2x^2yz+2xyz^2$$
Solution
We have the following like terms:
- $latex xyz^2~$, and $latex ~2xyz^2$
- $latex -2x^2yz~$, $latex ~4x^2yz~$, $latex -2x^2yz$
- $latex 5xy^2z~$ and $latex ~3xy^2z$
When we add these terms, we have:
$$(xyz^2+2xyz^2)+(-2x^2yz+4x^2yz-2x^2yz)+(5xy^2z+3xy^2z)$$
$$=3xyz^2+8xy^2z$$
Like terms – Practice problems
What is the coefficient of $latex x^2y$ when we combine like terms? $$2xy^2+2x^2y+3x^2y-4xy^2-3x^2y-xy^2-4x^2y$$
Write the value in the input box.
See also
Interested in learning more about like terms and algebraic expressions? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
